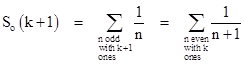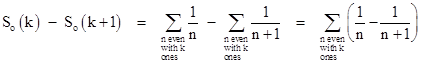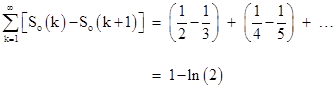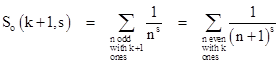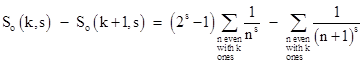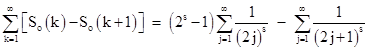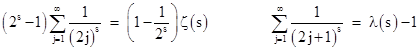Harmonic Sums of Integers With k Binary Ones

Let S_o(k) and S_e(k) denote the sums of the reciprocals of the odd and even natural numbers (respectively) whose binary representations contain exactly k ones. Thus we have

I conjectured that S_o(k) approaches ln(2) as k increases to infinity, whereupon Robin Chapman pointed out a simple proof involving some nice elementary manipulations of infinite series.

Let b(n) denote the number of ones in the binary representation of the positive integer n. If n is an odd integer with b(n) = k, then multiplying n by any power of 2 won't change the number of binary one bits, so b(2^tn) = k for any non-negative integer t. Thus, for each odd number n with b(n) = k there are infinitely many even numbers with the same number of one bits in their binary representations, of the form 2^tn with t = 1, 2, 3, ..., so the sum of their reciprocals is (1/n) times the factor 1/2 + 1/4 + 1/8 + ..., and this factor equals 1. Therefore, the sum of the reciprocals of all the odd numbers with exactly k one bits in their binary representations is equal to the sum of the reciprocals of all the even numbers with exactly k one bits. Thus we have

Also, since there is a one-to-one correspondence between the even integers n with k binary ones and the odd integers n+1 with k+1 binary ones, we can express S_o(k+1) in two different but equivalent ways

Making use of these relations, we have

To evaluate the sum of S_o(k) – S_o(k+1) over all positive integers k we need to evaluate the sum of (1/n) – 1/(n+1) over all even n, so we have

Notice that the left hand terms of the summation have the form

so the jth partial sum is just S_o(1) – S_o(j), and therefore the infinite sum is S_o(1) – lim{k→∞} S_o(k), which equals 1 – ln(2). Since S_o(1) is just 1, it follows that lim{k→∞} S_o(k) = ln(2). Also, since S_e(k) = S_o(k), the limit of the sum of the reciprocals of the natural numbers with k binary ones as k goes to infinity is 2ln(2).

Naturally if we consider the sum of reciprocals of the s powers of the natural numbers that have k ones in their binary representations, the limit as k goes to infinity must equal zero for integers s greater than 1, because (unlike the harmonic series with s = 1) the series converges, and as k increases we are taking a subset of the tail of the summation, which approaches zero. Still, it’s interesting to see if the above reasoning leads to this same conclusion. We can determine the limit, as k goes to infinity, of the sum of reciprocals of the s powers (for any positive integer s) of the natural numbers that have k ones in their binary representations. As before, we split the sum into odd and even components

and we let b(n) denote the number of ones in the binary representation of the positive integer n. Using the same reasoning as before, we note that if n is an odd integer with b(n) = k, then multiplying n by any power of 2 won't change the number of binary one bits, so b(2^tn) = k for any non-negative integer t. Thus, for each odd number n with b(n) = k there are infinitely many even numbers with the same number of one bits in their binary representations, of the form 2^tn with t = 1, 2, 3, ..., so the sum of the s powers of their reciprocals is (1/n^s) times σ = 1/2^s + 1/4^s + 1/8^s + .... From the relation

it follows that σ = (1/2^s)(1 + σ), from which we get σ = 1/(2^s – 1). Thus we have

Again, since there is a one-to-one correspondence between the even integers n with k binary ones and the odd integers n+1 with k+1 binary ones, we can express S_o(k+1,s) in two different but equivalent ways

Making use of these relations, we have

To evaluate the sum of S_o(k,s) – S_o(k+1,s) over all positive integers k we need to evaluate the sum of 1/n^s – 1/(n+1)^s over all even n. So, putting n = 2j, we have

The first term on the right side can be written as

where ζ(s) is the zeta function and λ(s) is the related sum of the odd terms of the zeta function. It is well known (and easy to show) that, for any integer s greater than 1 we have the relation

so it follows that, for any integer s greater than 1, we have

Again we observe that the left hand terms of the summation have the form

so the jth partial sum is just S_o(1,s) – S_o(j,s), and therefore the infinite sum is S_o(1,s) – lim{k→∞} S_o(k,s), which equals 1 for all integers s greater than 1. (We recall that it equals 1 – ln(2) for s = 1.) Since S_o(1,s) is just 1, it follows that lim{k→∞} S_o(k,s) = 0 for all integers s greater than 1. Also, since S_e(k,s) is proportional to S_o(k,s), we see that for any integer s greater than 1, the limit of the sum of the reciprocals of the s powers of the natural numbers with k binary ones as k goes to infinity is 0, as we knew it must be. Thus the case s = 1 is unique in giving a non-zero limit.

It’s well known that the zeta function has an analytic continuation, but it would be interesting to know if these specialized zeta functions S(k,s), consisting of just the terms of the zeta function with k ones in their binary representations, can be analytically continued. We might adopt the notation ζ_k(s) for these functions. We could also consider generalizing to other bases.

Return to MathPages Main Menu