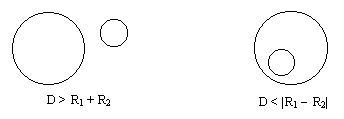White Ravens and Black Swans

According to the reductionist view, a linguistic description is identified with the thing or set of things it describes. For example, the expression "black swans" is identified with the intersection of the set of black entities with the set of swans, which in some regions may be the empty set. (Yes, there are black swans in a region of Australia, but for talking purposes we confine ourselves to regions in which there are none.) Likewise the expression "white ravens" is identified with the intersection of the set of white entities with the set of ravens, which (again) in some regions may be the empty set. Hence the extreme reductionist viewpoint would have us regard "black swans" and "white ravens", in regions where neither exist, as just two different descriptions of the same thing, namely, the empty set. Admittedly there's a sense in which this is true, but this reductionist interpretation fails to capture the full content of the descriptions.

In general there are infinitely many distinct ways of describing any given set. Some of the multiplicity of descriptions is simply due to different terms of expression having the same meaning. For example, "the even integers" and "the integers divisible by 2" are identical, and these two descriptions have (nearly) identical content, because the word "even" is essentially synonymous with "divisible by 2". On the other hand, given the sets A={1,3,5}, B={2,3,4}, and C={3,6,9}, the set {3} has the three descriptions A∩B, A∩C, and B∩C, and these are not just linguistically distinct, they are meaningfully distinct - in the same way that black swans are meaningfully distinct from white ravens - despite the fact that they may describe the same thing.

There's an interesting analogy between linguistic descriptions and mathematical specifications. Given an orthogonal coordinate system x,y, consider the intersection of the x axis (i.e., the locus y = 0) with the parabola whose equation is y = x² + 9. This parabola does not intersect with the x axis, so we've described the empty set. Likewise the intersection of the x axis with the locus y = x² + 4 is empty, so in a sense we might say these are two descriptions of the same thing. However, if we allow the coordinates of the intersection points to be complex, we find that these two descriptions do not describe the same thing, because one of them describes the set {[3i,0], [–3i,0]} and the other describes the set {[2i,0], [–2i,0]}. This is analogous to how "black swans" and "white ravens" can be said to describe different things if we expand the class of conceptual entities on which those descriptions operate.

What is the intersection of two circles that do intersect with each other? This may sound like a Zen riddle, but in fact every two (non-concentric) circles in the plane have two points of intersection, provided we allow the coordinates of the points to be complex. Let x₁,y₁ and x₂,y₂ denote the (real) coordinates of the centers of circles with radii R₁ and R₂ respectively, and let D denote the distance between the centers. The coordinates of the two points of intersection between these circles are given by

where A is the area of the triangle formed by the two circle centers and one of the points of intersection. The edge lengths of this triangle are D, R₁, and R₂, so the area is given by Heron's formula

In order for x and y to be real (for distinct centers), the area A must be real, which is the case if and only if

The two ways in which the circles may fail to satisfy this condition are illustrated below.

However, even in these cases, the two circles have two points of intersection, provided we define each circle to consist of all the pairs of complex numbers x,y that satisfy the respective circle equations. What we've shown above is just the intersection of each circle with the real plane P.  Conventionally when we refer to the intersection between two circles C₁ and C₂, we are considering only the intersections of C₁ and C₂ with the real plane P. In other words, we say "C₁ ∩ C₂", but we really have in mind "(C₁ ∩ P) ∩ (C₂ ∩ P)".

For example, someone may claim that the two circles "x² + y² = 9" and "(x - 4)² + y² = 4" have no intersection, because the distance between their centers exceeds the sum of their radii (as in the left-hand figure above), but then someone else falsifies this claim by pointing to the "black swan"

Is this just a linguistic problem? The first person may deny that this falsifies his original assertion, because the y value in this example is not a real number, but the second person will point out that the original assertion didn't specify real numbers, so this is a valid counter-example. Rather than discarding the original claim altogether, the first person will most likely just modify the statement, being careful now to restrict the variables to the class of real numbers. By doing this, he nullifies the counter-example and preserves most of the content of his original statement.

Similar circumstances can arise when dealing with claims about things in nature, such as the statement "all swans are white". Karl Popper famously used this as an example of a scientific statement which (he argued) is always exposed to the possibility of being falsified by the appearance of a black swan. Of course, if a black swan ever appears, the response of those who contend that all swans are white is likely to be similar to the response of our circle theorist. He will examine the "black swan" and find some disqualifying characteristic so that he can claim it is not a valid counter-example. He might find that this "swan" has been genetically altered or mutated, or been artificially dyed, or whatever. One of the shortcomings of falsificationism is that every assertion carries some unstated qualifications (analogous to the restriction to the real plane P in the above example), and we can always rescue a statement by adding qualifiers to exclude any counter-examples that arise.

For another - more realistic - example, consider Newton's first law of motion, which states that an object not subjected to any external force moves at constant speed in a straight line. Of course, most objects in our experience do not move at constant speed in a straight line, but we don't regard this as falsification of Newton's law, we simply infer that those objects are subject to forces, and we set about trying to identify them. This illustrates how Newton's law serves as an important organizing principle, and as such it is not falsifiable. Ultimately our knowledge of whether forces are being applied to an object is based on the observed behavior of the object, and Newton's first law of motion essentially says that objects move at constant speed in a straight line - except when they don't.

The tautological character of Newton's first law was criticized by the Austrian physicist Ernst Mach (1838-1916) in The Science of Mechanics. Mach was a positivist, believing that direct sense perceptions are (and must be) the basis of all knowledge, and he sought to eliminate what he regarded as metaphysical concepts (such as Newton's absolute space and time) from the foundations physics. His ideas inspired the "Vienna circle" of philosophers, who developed the doctrine of logical positivism in the 1920's, although they eventually rejected much of Mach's phenomenalism. Another Austrian, Karl Popper, then set himself the task of debunking the logical positivism of the Vienna circle, proposing falsification as the ultimate criterion for scientific theories. Ironically, Popper found himself widely identified with logical positivism, despite the fact that he regarded himself as its most strident opponent and critic.

Mach's writings also inspired Albert Einstein in his search for a general theory of relativity, and the young Einstein definitely had positivistic inclinations, although they were never as extreme as those of Mach himself. In fact, one of Einstein's great achievements was explaining how the hypothesis of atoms accounts for Brownian motion, and even describing how to infer the number of atoms in a certain quantity of matter based on the observable behavior of particles. However, since atoms were not directly observable, Mach regarded the idea as metaphysical rubbish. Nevertheless, Mach's skepticism and his rejection of "unmoved movers" had a powerful effect on Einstein, who initially regarded general relativity as the fulfillment of what he called "Mach's Principle". It came as a shock and disappointment to Einstein when he read the preface of Mach's last book (published posthumously by his son in 1921)

I gather that I am gradually becoming regarded as the forerunner of relativity... I must, however, as assuredly disclaim to be a forerunner of the relativists as I withhold from the atomistic doctrine of the present day.

In later years, as the principle of general covariance came to be better understood, it became clear that general relativity does not actually conform to Mach's ideals, or rather, it became clear that general relativity renders moot some of the issues that Mach regarded as crucial. Mach's Principle assumes a clear dichotomy between "things" (such as objects and fields) and the spatio-temporal relations between things, whereas in general relativity the metric of spacetime itself is a field, so the dichotomy breaks down. Spacetime itself is a dynamical element of the theory, no longer subject to the criticism of being an "unmoved mover". In this sense, Einstein believed he had answered the most cogent of Mach's criticisms of Newtonian space and time. However, on a more fundamental level, Einstein eventually rejected positivism in general, and Mach's Principle in particular, as he came to believe that scientific theories are ultimately free creations of the human mind, and that we cannot entirely dispense with "metaphysical" concepts. Einstein's conclusion was that "one should no longer speak of Mach's principle at all".

Likewise Popper's students, notably Imre Lakatos, came to repudiate flasification, and in turn their students repudiated the next generation of philosophies, and so on. It seems that no single philosophy of science is regarded as satisfactory for very long.

Return to MathPages Main Menu