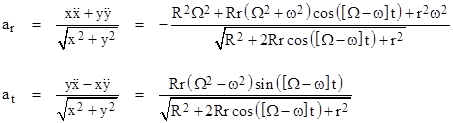The Moon Always Veers Toward the Sun

It's an interesting fact that the path of our Moon (with respect to the inertial rest frame of the Sun) always curves toward the Sun.  This might seem surprising at first, considering that the Moon revolves around the Earth, but it's not hard to show that, nevertheless, the Moon always has a positive acceleration toward the Sun.  In general, if we approximate the Sun's center as the inertial center of the solar system, and a planet's orbit as perfectly circular with radius R and angular speed Ω, and if this planet has a moon in a circular orbit of radius r and angular speed ω, then the coordinates of the moon (in the ecliptic plane) can be expressed as a function of the time t by equations of the form

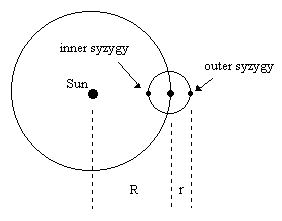
Notice that we have referenced the time coordinate  t = 0  to a moment of outer syzygy, i.e., a time when the Sun, planet, and moon (in that order) are aligned.  Taking curvature towards the Sun as positive, the maximum and minimum curvatures of this moon's path occur at the moments of outer and inner syzygy respectively, where the moon's acceleration reaches its extreme values, as illustrated below.

At the outer syzygy the two accelerations  Ω²R  and  ω²r  both point directly toward the Sun, so the total acceleration equals their sum, which is the maximum acceleration experienced by the moon.  At the inner syzygy the acceleration of the planet is still inward, but the moon's acceleration is toward the planet, which is outward.  As a result, the minimum acceleration (i.e., the most outward acceleration) experienced by the moon is equal to the difference Ω²R  - ω²r.  (This is also proportional to the geometric curvature of the path, because at this tangent configuration the y coordinate is proportional to the time coordinate, and the curvature here equals the second derivative of x with respect to y.)  Hence the necessary and sufficient condition for the moon to always be falling toward the Sun is for the radii and angular speeds to satisfy the inequality

From Kepler's law we know that for any gravitating mass m the angular speed of a satellite orbiting the mass is related to the radius r of the orbit by m = ω²r³, so the above inequality can be written in terms of the masses M and m of the Sun and planet as

Naturally these two quantities are proportional to the accelerations of gravity exerted on the moon by the Sun and the planet respectively.  (This just shows the correspondence between the inverse square law of gravity and Kepler's third law.)  From this relation, we see that for a planet of mass m orbiting the Sun at a distance R, a moon orbiting this planet will be always falling toward the Sun if and only if the radius of the moon's orbit exceeds a certain value, namely

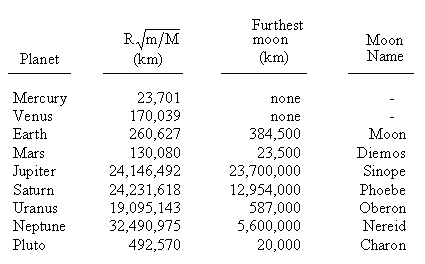
For each planet in the solar system with one or more known moon, this threshold value and the radius of the most distant moon are listed below.

This table shows that our Moon is unique among all the satellites of the planets, is so far as it is the only planetary satellite whose orbital radius exceeds the threshold value, which means it is the one satellite on which the Sun's gravitational acceleration exceeds the host planet's gravitational acceleration.  Consequently, it is the only moon in the solar system that is always falling toward the Sun.

It's interesting that Jupiter's 16 satellites have orbits that range from just 128,000 km up to 23.7 million miles, which is almost exactly equal to the threshold radius.  Saturn's many moons and rings occupy the radial distance from 137,000 km up to about 13 million km, which is a little more than half the threshold radius.  This, combined with the fact that all the other moons in the solar system (excluding our own Moon) lie within their respective threshold radii suggests that this radius constitutes a rough natural limit to the size of the satellite orbits around planets in our solar system.  It stands to reason that most stable moons would be situated in orbits such that the gravity of the host planet is stronger than the Sun's gravity, because otherwise there would be a tendency for the bodies to become separated.  Jupiter's size and its proximity to the asteroid belt probably accounts for the fact that its orbit space is fully populated, right up to the gravitational threshold.

The anomaly in this theory is our own Moon, which presently orbits significantly outside the Earth/Sun gravitational threshold radius.  However, the Moon's orbit was originally much closer to the Earth, and it is gradually receding from the Earth as our system radiates energy due to friction caused by tidal effects.

It's tempting to try applying this analysis to the solar system itself relative to the Milky Way galaxy.  The mass of our galaxy is estimated to be about 10¹² solar masses, and the distance from our Sun to the galactic center is about (1.8)10⁹ astronomical units, so if we assumed the entire mass of the galaxy was concentrated at its center and the Sun was in orbit around this center, the threshold radius would be roughly 1800 AU.  The radius of Pluto's orbit is about 39 AU, so this is well inside the threshold (by a factor of about 45).  However, the mass of our galaxy is actually distributed over a disk-like region with distinct spiral arms, so there is a much greater local gravitational acceleration from surrounding stars than if all the mass was at the center.  This will reduce the 1800 AU threshold significantly (possibly by a factor near 45?).

In the preceding discussion we gave just the minimum and maximum accelerations, but it isn’t difficult to give an explicit expression for the acceleration at any point along the moon’s path. First we note that the distance ρ from the moon to the Sun is given by

The components of the acceleration vector of the moon are simply the second derivatives of the position coordinates

where dots signify derivatives with respect to time. To express this acceleration vector in terms of its purely radial and tangential components, we can take the dot product with the position vector and with a perpendicular vector, respectively. Thus we have

Inserting the expressions for x, y, and their derivatives, this gives

As a check, by replacing the sine in the expression for a_t with the square root of 1 minus the cosine, we can easily verify that

For the parameters of the Earth-Moon system, the only real maxima and minima of a_r occur when the cosine in that expression equals +1 or –1, where we have

in agreement with our previous assessment.  The radius of the Earth’s orbit around the Sun is roughly (1.5)10¹¹ meters, the radius of the Moon’s orbit around the Earth is about (3.85)10⁸ meters, the angular velocity of the Earth’s orbit is (1.99)10^–7 rad/sec, and the angular velocity of the Moon’s orbit is (2.4)10^–6 rad/sec, so even at the inner syzygy the radial acceleration is negative (i.e., inward toward the Sun), with a value of –(3.7)10^-3 m/sec².

Return to MathPages Main Menu