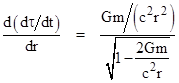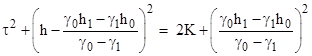Accelerating in Place

With respect to a local inertial coordinate system at any point on the Earth's surface, the surface is accelerating outward at 9.8 m/sec², and yet the radius of the Earth is (fairly) constant.  It might seem as if these two facts conflict with each other, but they can be reconciled if we allow local variations in the metric of spacetime, which effectively permits variations in the rate at which time advances. 

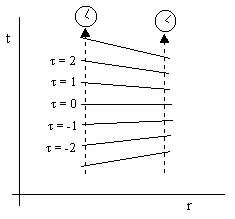
Imagine two ideal clocks near the Earth's surface, positioned so that one is directly above the other, separated by a distance of 1 meter.  At any arbitrary time we can "synchronize" the two clocks, so they both read t = 0, using some standard and repeatable method, such as the receipt of light pulses emitted from the mid-point between them.  Then, after one second has elapsed on the upper clock, the same procedure can be used to compare the readings on the clocks, and we find that the lower clock shows an elapsed time of slightly less than one second.  This has been confirmed by observations of the red-shifted frequencies of light emitted from characteristic processes in strong gravitational fields near stars, as well as in terrestrial experiments.  The lapse of proper time along a worldline at a fixed radial position near a gravitating body of mass m is lower than for worldines further from the body.  Quantitatively, the derivative of proper time with respect to Schwarzschild coordinate time at a fixed radius r in a spherically symmetrical static field is

where G is Newton's gravitational constant and c is the speed of light with respect to local inertial coordinates.  Roughly speaking, we can imagine lines of constant proper time (for worldlines of fixed radial position) drawn on a graph of coordinate time versus radial distance, as shown below.

What effect does this variation in the lapse of proper time versus radial distance have on the behavior of test particles in this region?  It might be tempting to think that a free particle, being a geodesic in spacetime, would accelerate outward, so that its worldline maintains a constant angle relative to the lines of constant proper time.  Indeed this would be the case if the signature of the Minkowski metric was positive.  However, the signature is actually negative, which explains why the timelike extremal (i.e., geodesic) paths of free particles in spacetime follow curves that maximize (rather than minimize) the lapse of proper time.  The line element on one radial ray is of the form

where g_tt is independent of t.  This relationship between the three differentials dt, dt, and dr can be re-arranged into the form

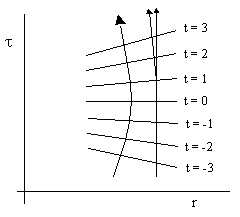
Since the geodesic paths on the manifold are strictly a function of the relation between the differentials, and how this relation changes with variations in r, it follows that we get the same timelike geodesics by minimizing (dt)² as we do by maximizing (dτ)².  (This works only because this particular system of coordinates gives metric coefficients that are independent of the time coordinate.)  This suggests plotting a small region of the r,t plane with vertical lines of constant r, but with the lines of constant t (relative to some arbitrary reference time) slanted so that the vertical height corresponds to the proper time t along a stationary worldline, as illustrated below.

Notice that a stationary worldline is perpendicular to the t = 0 locus, but for subsequent values of t the lines of constant t are sloped progressively inward.  In order to minimize the lapse of the time coordinate t, a free-falling particle would remain always perpendicular to the lines of constant t.  This implies that the local inertial reference frame is accelerating inward, and as a result, a stationary worldline is constantly accelerating outward relative to the local inertial reference frame.  (We're using the term "local inertial reference frame" here to signify, at any given point, the class of local inertial coordinate systems moving uniformly in a straight line with respect to each other.  In general these coordinate systems cannot be extended globally, due to the curvature of the manifold.)

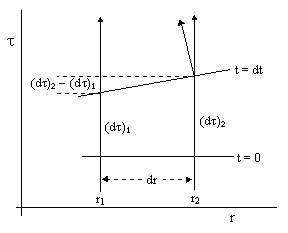
The effective acceleration of a stationary worldline with respect to the local free-falling inertial reference frame can be deduced based on how rapidly the lines of constant t are slanting inwards.  If we consider two neighboring stationary worldlines, separated by an incremental radial distance dr, the lapse of proper time dt for a given incremental lapse of coordinate time dt is less for the inner worldline than for the outer worldline, as illustrated below.

The amount of this difference can be found by differentiating equation (1) with respect to r, which gives

The denominator of the right side is virtually 1 for typical distances, so we can take just the numerator, and multiply through by dr to give the change in dt for a given dt and dr:

The slope of the locus t = dt is given by dividing this difference by dr, which gives a quantity with units of sec/meter.  In order for a worldline at t = dt to be perpendicular to this locus, it must have the perpendicular slope, which is the same quantity converted from units of sec/meter to units of meter/sec.  This is accomplished by multiplying through by c², and the result is the incremental change in velocity for an incremental time dt.  Dividing by dt gives the acceleration of the stationary worldline at r₁ relative to the local inertial reference frame

With the gravitational constant G = (6.67)10^-11 Nm²/kg² and the Earth's mass m = (5.98)10²⁴ kg and the Earth's mean radius r = (6.37)10⁶ m, we find the outward acceleration of stationary worldlines at the Earth's surface is approximately 9.8 m/sec².

The fact that the geodesics of spacetime in a spherically symmetrical gravitational field can be found by minimizing the Schwarzschild coordinate time t can be regarded as a confirmation (and even an extension) of Fermat's Principle of Least Time, but of course it doesn't apply for arbitrary time coordinates.  It works only because the coefficients of the Schwarzschild line element are independent of this particular time coordinate.  For more on this, see Path Lengths and Coordinates.

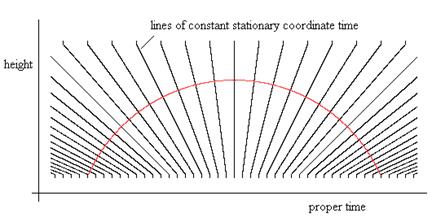
Incidentally, to construct a simple illustration of an approximate low-speed ballistic trajectory in a uniform gravitational field, let t denote a stationary time coordinate (such as the Schwarzschild coordinate time) in terms of which the rates dτ/dt of proper time with respect to coordinate time at the fixed heights h₀ and h₁ are γ₀ and γ₁ respectively, and assume the rate varies linearly between these two heights.  On a plot of height versus proper time (for a particular trajectory) the lines of constant coordinate time are radial rays through a single point, so the trajectory is a segment of the circle

A plot of this trajectory for a typical case is shown below.

Return to MathPages Main Menu