Preserving the Wave

One of the main features of modern science has been the search for symmetries, such as transformations that leave some fundamental properties or qualities unchanged. For example, Galileo observed that the laws of mechanics are invariant (up to the resolution he was able to measure) under any transformation of the spacetime coordinates of the form x′ = x−vt and t′ = t. Subsequently this transformation was modified so that the symmetry encompassed the laws of electrodynamics as well. The necessary modification can be inferred from the wave equation, which, in one space dimension, is

where the units of x and t have been chosen so that the speed of the wave front is unity. The general solution is

where f and g are arbitrary functions. The two components are called the retarded and advanced solutions respectively. Clearly a Galilean transformation does not preserve the wave equation, because the arguments of these two functions transform into x′+vt′−t′ and x′+vt′+t′ respectively. This was to be expected, since the wave equation is symmetrical in t and x, whereas Galileo's transformation is not. In the 1880's Voigt noticed that the wave equation is preserved under a transformation of the form x′ = γ(x−vt), t′ = γ(t−vx) where γ is any constant. This can be confirmed by observing that x−t = (x′−t′)/(γ(1+v)) and x+t = (x′+t′)/(γ(1−v)), which shows that for any fixed v the functions of x+t and x-t can be expressed as functions of x′+t′ and x′−t′ respectively. Furthermore, if we set γ = 1/(1−v²)^1/2, the reciprocal transformations are identical (up to the sign of v), and Voigt's transformation becomes Lorentz's, which is the basis of special relativity. Thus, in a sense, special relativity can be regarded as having been founded on the principle that all systems of coordinates preserving the wave equation with wave speed c are equally suitable for the representation of physical phenomena. (If c were infinite, this would agree with Galileo's principle.)

In the general theory of relativity the principle of Lorentz symmetry is strictly valid only locally in the neighborhood of each event, and the class of coordinate transformations suitable for simple expression of physical laws is enlarged to include all those within a single diffeomorphism equivalence class. This is a significant extension, although it is still just a very small fraction of all possible coordinate transformations that preserve the light cone structure emanating from a given worldline if we do not require diffeomorphic images.

We distinguish here between coordinate transformations that leave the wave equation itself unchanged, and coordinate transformations that map a certain set of solutions of the wave equation to itself. For example, consider the set of all spherically symmetrical solutions of the wave equation centered at the origin of an inertial coordinate system x,y,z,t. The standard equation of a spherically symmetrical wave in three spatial dimensions is

where (again) the units of r and t have been chosen so that the speed of the wave front is unity. If we define ϕ(r,t) = r ψ(r,t) the wave equation can be written in the form

from which we get the general solution

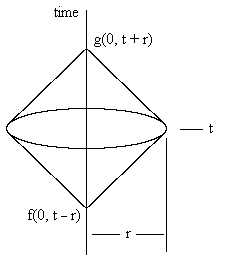
where the functions f and g are completely arbitrary. The boundary conditions are provided by the values of f(0,t) and g(0,t) at the spatial origin (0,t). Each event at the origin is surrounded by an expanding spherical shell of ψ values that diminish in inverse proportion to r. (The value of ψ goes to infinity at r = 0.) At any given event (r,t) the value of ψ is determined by the value of f at the origin at time t − r and the value of g at the origin at time t + r, as illustrated below.

The entire solution can thus be defined by the two one-dimensional functions f(0,t) and g(0,t), and these are totally arbitrary functions. In fact, they need not even be continuous.

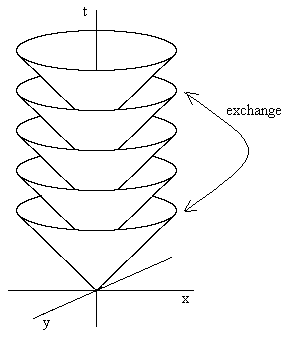
If we focus on just the retarded solution, a spherically symmetrical wave emanating from the spatial origin can be regarded as a series of wave shells as illustrated below (showing just two spatial dimensions). On each shell the wave function at the radius r and time t is equal to f(0,t−r)/r.

Each shell is independent of all the others (Huygens' Principle), so the wave equation for light waves emanating from a single worldline partitions spacetime into an ordered sequence of mutually exclusive sub-spaces. Given any such series of retarded wave cones satisfying the wave equation for the boundary conditions f(0,t), we arrive at another valid spherically symmetrical wave solution if we exchange (transpose) any pair of shells. It follows that any permutation of these retarded wave cones leads to another valid sequence of wave cones, still satisfying the wave equation, because the function f is arbitrary. Of course, the boundary conditions at the spatial origin are also being permuted, so it can be argued that these are physically distinct conditions, both of which happen to satisfy the wave equation. However, more fundamentally, the physical distinctness of these permutated solutions can be questioned, because it can be regarded as merely an artifact of our coordinate system. In other words, it can be argued that permutation of the wave cones is simply a descriptive change, because they are simply transformations of the coordinate system. Admittedly, these transformations are discontinuous, but our prejudice against discontinuous transformations may be compared to the earlier prejudice against non-linear transformations, which was shown by general relativity to be unjustified.

The question, then, is whether the transposition of two infinitesimal light cones preserves the suitability of the coordinate system for the description of physical phenomena. In one sense, any arbitrary one-to-one mapping between four-tuples (t,x,y,z) of real numbers and the events of spacetime is a viable system of coordinates, but we intuit that most of these mappings would not facilitate any simple expression of physical laws. For example, if we identify the particle appearing at a certain aggregate of events as "the same particle", we wish to use a system of coordinates such that this aggregate of events is assigned a numerically continuous locus of four-tuples. At the classical level, there seems to exist (perhaps surprisingly) a single system of space and time coordinates in terms of which every individuated physical object occupies a numerically continuous locus of events, although it can be argued that this is actually a definition rather than an observation, because we infer the individuations of objects from the continuity of their spacetime loci. Nevertheless, it is a remarkably successful organizing principle - at the classical level.

However, the classical individuation of particles breaks down in the realm of elementary particles and quantum mechanics. Here we find that (for example) the wave functions of two identical electrons in a box overlap, so when an observation of one of these particles is made we cannot say for sure which of the two particles has been observed. Hence the particles do not possess classical trajectories, nor is it even possible to absolutely individuate them. This indistinguishability has observable consequences, such as in the thermodynamic properties of fermions and bosons, because when counting the numbers of distinct configurations of particles in each energy state we must correctly account for the indistinguishability of the particles. (This behavior is crucial for the operation of lasers.)

Setting aside quantum phenomena, we have the classical criterion that our coordinate system should be such that the locus of events associated with each individual object is contiguous, but there is another classical criterion, which might be called the "causal ordering" criterion. Originally it was believed that the set of spacetime events possessed an absolute and complete causal ordering, in the sense that every suitable system of space and time coordinates would agree on the temporal and causal precedence between any two given events. However, the coordinate systems of special relativity do not fulfill this requirement for absolute temporal ordering, because it is possible, given two events A and B, for event A to have a numerically smaller value of t than event B with respect to one system of coordinates, but for this relation to be reversed with respect to another equally valid system of coordinates. Thus the set of coordinate systems related by the Lorentz transformation provides only a partial ordering of events. Nevertheless we find that arbitrary inertial coordinate systems (related by Lorentz transformations) are entirely suitable for expressing the laws of physics. In fact, they permit a simpler expression than do coordinate systems with a total temporal ordering, although it took even the best physicists of the early 1900's several years to recognize this fact.

As noted previously, the Lorentz transformation arises from consideration of the wave equation, and the suitability of the coordinate systems related by these transformations is based on the fact that a wave (i.e., a field distribution satisfying the wave equation) with respect to one such system is a wave with respect to all such systems. This raises the interesting question of whether other transformations that preserve waves may also lead to useful coordinate systems - even if they do not preserve some of the other attributes that have traditionally been required for physically perspicuous coordinate systems (just as total temporal ordering was given up in special relativity). In particular, it's interesting to consider whether a transformation that permutes the retarded wave cones of a spherically symmetrical sequence of waves leads to a useful representation of the causal relations between events. In effect, each cone is an entire wave, emanating from the origin out to infinite radial distance, so by permuting cones we are keeping each wave (centered at the origin) intact. Also, even if we regard a sequence of shells as a single entity, this entity remains on a numerically contiguous locus of coordinates after permuting cones. Thus the individuation of the emitting worldline is preserved.

Of course, unlike the Lorentz transformations, a permutation of light cones does not preserve the identity of all worldlines, it preserves only the emitting wordline and those parallel to it. In general, the usual objection to discontinuous transformations of the spacetime coordinates is that they violate the topology of the manifold, in the sense that the open sets and neighborhoods of the manifold are not preserved. On the other hand, even the Lorentz transformation leads to non-Hausdorf topology if we take the invariant spacetime interval as the measure of proximity, because of the singularity of this measure along light rays. In addition, the freedom to allow curvature of spacetime in general relativity permits global topologies that would be inconceivable for flat manifolds, but that may nevertheless be physically meaningful.

It's interesting to apply the idea of wave cone permutation to the task of postdiction. We're immediately led to the idea that only retarded waves can be physically realized, because any permutation of the retarded waves would not preserve the advanced waves. In addition, we would expect spacetime to have three spatial dimensions (or perhaps some higher odd number), because only in this case does Huygens' Principle apply, enabling the light cones to be mutually exclusive subspaces. We would also be led to the idea of temporal symmetry along individual worldlines, because this is represented by the reversal permutation. In other words, essentially the same physical laws can be applied to the description of physical phenomena under either of these two arrangements of the light cones (neglecting the current interpretation of how certain mesons decay). If these two extreme permutations can be encompassed by the same physical laws, what about all the other permutations? Is there a useful and/or meaningful way of expressing the laws of physics in such a way that they apply equally well with respect to any system of spacetime coordinates that is related to a conventional inertial coordinate system by an arbitrary permutation of the sequence of light cones emanating from any given geodesic worldline?

Return to MathPages Main Menu