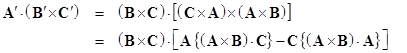|
Quarky Volume Formula for Parallelepiped |
|
|
|
Beginning with the ubiquitous triple product identity |
|
|
|
|
|
|
|
for vectors in R3, we immediately have the handy formula for the cross product of two cross products |
|
|
|
|
|
|
|
Now suppose we define three new vectors in terms of A, B, C as follows |
|
|
|
|
|
|
|
It's well known that the triple product A' ∙ (B' x C') is simply the square of the triple product A ∙ (B x C). To see why this is true, notice that using (2) the "primed" triple-product can be expressed as |
|
|
|
|
|
|
|
Since the quantity (A x B) ∙ C equals the volume of the parallelepiped with the vectors A, B, C forming adjacent edges, it's clear that (A x B) ∙ A = 0, because two of the three edges are identical. Thus the right-most term in the preceding expression drops out, and the resulting quantity is simply (B x C) ∙ A[(A x B) ∙ C], which, in view of associativity of scalar multiplication over the dot product, is the same as [(B x C) ∙ A][(A x B) ∙ C]. Both factors equal the volume of a parallelepiped with edges A, B, C, so the product equals [A ∙ (B x C)]2. |
|
|
|
But this is not very elegant. Of course, in the special case when A, B, C are mutually orthogonal it follows that the pairwise perpendicular vectors A’, B’, C’ are also orthogonal, and so the two triple products are just the volumes of two rectangular solids, one with sides A, B, C and the other with sides A' = BC, B' = AC, C' = AB, from which it's obvious that the second volume is the square of the first. This is based on the volume formula V = |A||B||C| for rectangular solids, and the same degree of obviousness could be achieved in the general case if we had a suitable formula for the volume of a general parallelepiped. |
|
|
|
The triple product A ∙ (B x C) corresponds to the volume of a general parallelepiped with adjacent edges A, B, C, and this volume can be expressed by the formula |
|
|
|
|
|
|
|
where S is the product of the sines of the pairwise angles θAB, θBC, θCA between the vectors A, B, C, and S' is the product of sines of the angles θA’B’, θB’C’, θC’A’ between the dual vectors A’, B’, C’. (This formula can be verified by substituting the vector expressions for S and S'.) Likewise the volume of the dual parallelepiped is |
|
|
|
|
|
|
|
The magnitudes of the primed vectors are |
|
|
|
|
|
|
|
so we have |
|
|
|
|
|
It's interesting how the 2/3 and 1/3 exponents on S and S' seem to mimic the combinatorial behavior of the properties of quarks. It's also interesting that S1/3 is just the geometric mean of the three pairwise sines, so if we imagined a rectangular solid with edge lengths equal to the three sines, the quantity S1/3 would be the edge of a cube with the same volume. |
|
|