Gamaliel's Principle

The new testament tells of how, after the apostles were imprisoned in Jerusalem, they were brought before the council of high priests, who questioned them about why they had disobeyed the order to stop preaching the word of Jesus.  Peter's response was "We ought to obey God rather than men. The God of our fathers raised up Jesus, whom ye slew and hanged on a tree". This explanation apparently didn't appease the high priests, so they "took counsel to slay them [the apostles]".

Then stood there up one in the council, named Gamaliel, a doctor of the law, high in reputation among all the people, and he said unto them: Take heed of yourselves what ye intend to do as touching these men. For before these days rose up Theudas, boasting himself to be somebody; to whom a number of men, about four hundred, joined themselves; he was slain, and all, as many as obeyed him, were scattered and brought to nought. After this rose up Judas of Galilee in the days of the taxing, and drew away much people after him; he also perished, and all, even as many as obeyed him, were dispersed. And now I say unto you, refrain from these men, and let them alone, for if this counsel or this work be of men, it will come to nought: but if it be of God, ye cannot overthrow it, lest haply ye be found even to fight against God. (Acts 5:34)

This is an interesting line of reasoning, from more than one point of view. It might be compared with the (probably apocryphal, but still useful) story of Caliph Omar's decision to burn the library of Alexandria, considering that every book contained therein must either be heretical or else redundant to the Koran. Indeed, if Gamaliel had left out the last phrase of his argument, it could have been taken as an argument for slaying the apostles, because if what they are preaching is false, they deserve to be slain, whereas if what they are preaching is true, slaying them can do no harm, i.e., "if it be of God, ye cannot overthrow it". The argument is turned around only by the final phrase "lest haply ye be found even to fight against God". Although the wording (in this King James translation) is somewhat obscure, the point seems clear enough: if it so happens that these men really are of God, then slaying them might be - let us say - short-sighted. This is reminiscent of "Pascal's wager", i.e., the argument made by Blaise Pascal on pseudo-mathematical grounds that a man ought to bet on the existence of God and lead a good life that will gain him entrance to Heaven, because if he's wrong it doesn't matter, whereas if God really does exist, then clearly the "return" on his wager is infinite.

However, while the arguments of Omar and Pascal were both parochial (and easily criticized on grounds of circularity), the principle put forward by Gamaliel is both more universal and more interesting. It's premise is that the long-term course of future events - consequent to a particular antecedent event - is strictly correlated with the truth quality of the antecedent event. Thus the answer to the question of whether or not "this work be of men or of God" is to be found, according to Gamaliel's principle, in the future course of events, exactly opposite the usual convention of seeking definitive information about a particular event in the "causal past" of that event, i.e., the course of prior events leading up to the event in question. Rather than inquiring into the background of Mary and Joseph of Nazareth, for example, Gamaliel tells us that the truth about Jesus depends on the consequent events that transpire in the future.

Gamaliel's principle can be compared to Aristotle's famous remark that we should not count a man happy (blessed?) until he is dead, recognizing that the meaning and truth of the events in a man's life may not be evident at the time of occurrence, but may become clear in the future. This was one of the principles of Greek tragedy.

In physics we're familiar with two different kinds of processes, or rather, two different kinds of descriptions. On the most detailed level, we generally find that our descriptions of physical processes can be temporally reversed and still conform to the same "laws", whereas on a higher (coarser) level, our descriptions are generally not reversible with respect to our higher-level "laws". Formally, if p(t) denotes the state of a system at time t (for some suitable foliation), then the physical "law" governing the behavior of this system is typically expressed as a function L such that L[p(t)] = 0, and the process (with respect to this law) is temporally reversible if and only if L[p(t)] = 0 implies L[p(–t)] = 0. We also note that our local laws are generally symmetrical under temporal translation as well, i.e., L[p(t)] = 0 implies L[p(t+k)] = 0 for any constant k.

On a thermodynamic level, where we describe aggregated states in terms of bulk equilibrium parameters such as "temperature", the physical laws expressed in terms of these bulk parameters are generally not reversible. In fact, not only does a time-reversed sequence of events (in terms of the bulk parameters) fail to satisfy the forward physical laws, it often is not even possible to infer prior states of a system from knowledge of subsequent states. This is basically because the individual positions and momenta of the various parts of the system are not carried along in the bulk representation. Instead, the thermodynamic trajectory of a system is defined in terms of means of the detailed trajectories, and the mapping between sets of specific elements and the means of such sets is obviously not one-to-one. Each mean state corresponds to a large number of specific states, i.e., to a large number of distinct sets of detailed trajectories, and the subsequent mean states are, in a sense, the average of all the configurations that would be produced by the individual trajectories. As a result, the mean state has a strong tendency to evolve in the direction that maximizes the number of represented detailed states. This implies that a system progresses from any of a large number of specialized states to one of a much smaller number of more general states, and it follows that each state usually has multiple possible predecessors. Hence, knowing the current (mean) state, we cannot uniquely infer the prior states.

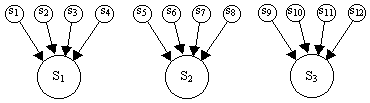
How does this relate to Gamaliel's principle? These considerations might seem to suggest that the future course of events cannot form the basis of a definition of any prior event. The tendency for entropy to increase seems to imply a lack of sensitivity to initial conditions, because it tells us that a large number of possible prior states all lead to the same subsequent state, as indicated schematically in the figure below.

However, this runs counter to the fact that many physical processes, including macroscopic ones, exhibit extremely high sensitivity to variations in initial conditions. Indeed, just as we're unable to uniquely infer the past from the present, we are also, at least as a practical matter, unable to uniquely infer the future - despite the fact that the above schematic seems to suggest that predicting the future should be relatively easy. The appearance of new specialized structures seemingly contrary to the direction of overall state evolution implied by the second law of thermodynamics has often been discussed. Part of the explanation for this apparent paradox is that the above schematic is misleading, because it pictorially suggests a certain set of proximity relations between the prior states s₁ through s₁₂. For example, it suggests that states s₁ and s₂ are "neighbors" within the state space, whereas it's entirely possible for (say) s₁ and s₉ to be arbitrarily close neighbors, even though they lead to very different successor states. Thus, the mere fact that there is a many-to-one mapping of past to future states does not rule out arbitrarily great sensitivity of the future state to very small changes in the prior state.

Another subtlety in the interpretation of thermodynamic laws is due to the arbitrariness in our choice not only of how to partition the phase space into elementary "cells" (which are presumed equally probable), but also in our choice of which cells to combine into macrostates. Admittedly in the context of quantum mechanics it seems natural to define the cells with volume (Dx)(Dp) » h, but this still leaves the shape of a cell to be chosen. The arbitrariness in the definition of our macrostates is sometimes said to be unimportant, because the vast majority of the entropy of macrostates is due to detailed variations on a scale far below the resolution of our senses. However, this is really just an explanation for why we (human beings) partition the phase space in a certain way; it doesn't imply that our choices have any absolute significance beyond expressing the limitations of our senses and our minds.

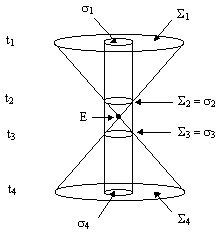
It's also important, when evaluating the flow of implication between events, to clearly delineate the relevant context and scope. There is a psychological tendency to limit our view of the context of an event E to a cylindrical regions, i.e., a region of fixed spatial extent, as shown in the figure below, whereas in fact the relevant context is the lightcone with vertex E, emanating outward in both the past and future directions.

At the prior time-slice t₁ the complete context of event E is the entire region Σ₁ contained within the past light cone, so any extrapolation on the basis of the region σ₁ inside the cylinder is bound to be under-determined. Only within the short span of time t₂ to t₃ can we be sure that the cylinder provides the most complete possible basis for evaluation. Likewise at the subsequent time-slice t₄ the complete context is Σ₄, so any attempt to uniquely infer event E purely on the basis of σ₄ is bound to fail.

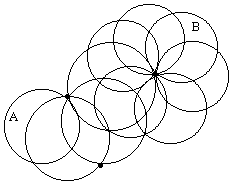
The situation is further complicated by the overlap of the lightcones of different events. It's interesting to compare this with the concept of analytic continuation of functions in the complex plane. We can expand a function in the neighborhood of a given point into a power series that converges on the disk centered at the given point and with a radius that extends to the nearest pole of the function. This limits the range of a convergent power series about that point, but we can develop another power series about any point in that convergent disk, and this gives another convergent disk that partially overlaps with the first, but that extends beyond the first. Repeating this process we can analytically continue the function to cover the entire complex plane, excluding the poles. The figure below illustrates this process in the neighborhood of three poles.

The continuation from one point to another is not necessarily unique, because even though each pair of adjacent continued disks have identical values in their region of overlap, and each disk is uniquely determined, the continuation from disk A to disk B (for example) depends on which path is followed through the poles. In fact, simply winding around a single pole will, in general, lead to different values (which is why Riemann surfaces on the complex plane are multi-valued). This just illustrates one way in which the conditions inside overlapping light-cones (projected onto a suitable time slice) might be combined in non-trivial ways. (What sort of singularity in spacetime could play the role of the "poles" in complex function theory?) Compare this with the no-curvature interpretation of general relativity, and also with the global reversibility of cellular automata.

Oddly enough, the same Gamaliel who interceded on behalf of Peter and the apostles later played an indirect role in preventing Paul from being slain. This was in Jerusalem, after Paul had begun preaching to the Gentiles, letting Greeks and others into the temples. Certain factions felt that Paul was blaspheming and polluting the holy places

...the people ran together, and they took Paul, and drew him out of the temple, and forthwith the doors were shut. And as they were about to kill him, tidings came unto the chief captain... that all Jerusalem was in an uproar... [he] immediately took soldiers and centurions and ran down unto them. And when they saw the chief captain and the soldiers, they left beating Paul.

The chief captain, unable to get a clear explanation of what the uproar was all about, decided to take Paul away, but Paul asked if he could be permitted to speak to the crowd. He was given leave to do so, and delivered a speech (Acts 22) that might have been one of Shakespeare's inspirations for Marc Antony's "Friends, Romans, Countrymen" oration to the mob in Julius Caesar:

Men, brethren, and fathers, hear ye my defense which I make now unto you. I am verily a man which am a Jew, born in Tarsus, brought up in this city [Jerusalem] at the feet of Gamaliel, and taught according to the perfect manner of the laws of the father, and was zealous toward God as ye all are this day. And I persecuted this way unto the death, binding and delivering into prisons both men and women... And it came to pass that, as I was come nigh unto Damascus about noon, suddenly there shone from heaven a great light round about me. And I fell unto the ground, and heard a voice saying unto me, "Saul, Saul, why persecutest thou me?"

Unlike Marc Antony, Paul failed to win over the crowd with his performance, although subsequent reviews have been more favorable. From a strictly tactical standpoint, the reference to Gamaliel here is slightly puzzling, because Paul's intent was clearly to begin by re-assuring the crowd of his impeccable pedigree, his solid grounding in "the laws of the father", and even pointing out that he had been a zealous persecutor of the followers of Jesus. If it was remembered that Gamaliel had literally saved the lives of Peter and the other apostles of Jesus, it would be strange for Paul to cite Gamaliel - in effect, a known sympathizer - at that point in his address. Perhaps the earlier incident was not considered significant, i.e., it may have been one of those things that only in retrospect is seen to have been important.

In any case, the whole history of Christianity (from our present point of view) stands as a remarkable example of how events can be imbued with meaning and significance by the consequent as well as the antecedent conditions. St. Augustine conveyed a sense of the possibilities when he wrote that "Surely God created heaven and earth not in time, but together with time."

Return to MathPages Main Menu