Equal Bisectors and Isosceles Triangles

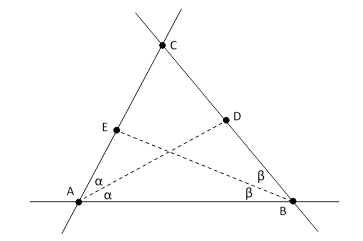
Given a triangle ABC, draw a line through A bisecting the angle between the lines AB and AC, and let D denote the point where this line intersects the line BC. Similarly draw a line through B bisecting the angle between the lines BA and BC, and let E denote the point where this line intersects the line AC. An example of such a construction is shown below.

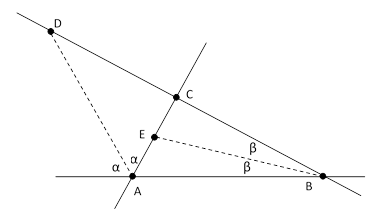
It seems intuitively obvious that if the lengths of the segments AD and BE are equal, then ABC is an isosceles triangle with the base AB. However, this proposition is not trivial to prove. In fact, as stated, it’s actually false, because we haven’t fully specified the construction. Every pair of intersecting lines has two distinct bisectors (perpendicular to each other), and we haven’t specified which of the bisectors to choose. To illustrate how this affects the result, consider the triangle ABC formed by three intersecting lines shown below.

In this case the segment AD bisecting the lines AB and AC has the same length as the segment BE bisecting the lines BA and BC, so the stated conditions are all met, and yet the triangle ABC is obviously not isosceles. Of course, we implicitly intended for the lines AD and BE to bisect the “interior” angles at their respective vertices, which is to say, we require that the point D be situated between B and C, and that the point E be situated between A and C. These “betweenness” conditions weren’t specified in our original problem statement. (The lack of betweenness axioms was also a deficiency in Euclid’s Elements.) Since the truth of the proposition depends on this subtle concept, it isn’t surprising that the proof is not entirely trivial.

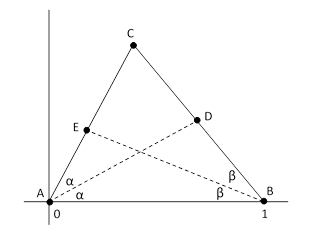
To prove the proposition, place the triangle in a Cartesian coordinate system such that the segment AB coincides with the unit segment from (0,0) to (1,0) as shown below, and suppose both of the bisectors have length L.

In general, the angle bisectors strike the opposite sides at the points [Lcos(α), Lsin(α)] and [1–Lcos(β), Lsin(β)], so we have

Equating the values of 1/L implied by these two equations gives

which, in terms of just the parameters a = cos(α) and b = cos(β) can be written as

Obviously a = b is a solution, corresponding to the isosceles cases, but this still leaves the other possible roots of the right hand factor, i.e., values of a,b such that

This equation can be written in the form

The quantity under the square root is the product of 1–a² and 1–b², and since a and b are the cosines of α and β, these terms are just the squares of the sines, so the above equation can be written as

Using the addition rule for cosines, this reduces to

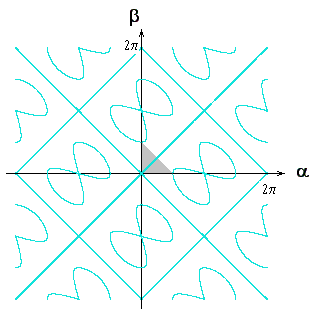
Together with the "isosceles factor", cos(α) – cos(β), this completely describes all sets of three co-planar lines L₁, L₂, L₃ such that the distance from the intersection of L₁, L₂ along an angle-bisector of those lines to the line L₃ equals the distance from the intersection of L₂, L₃ along an angle-bisector of those lines to the line L₁. A plot of the locus of angle α,β that satisfy this equation is shown below.

Without loss of generality we can require that both α and β are positive, and the requirement for “betweenness” implies that 2α + 2β is less than π (meaning they are interior angles of a triangle), so we have the condition α + β < π/2. This region is shown as a shaded area in the figure above. Note that the “figure eight” loci intersect the axes at π/2. Hence, within this region, the only solutions are α = β. By Proposition 6 of Book I of Euclid’s Elements, it follows that the sides opposite these angles are equal, so the triangle is isosceles.

Return to MathPages Main Menu