The Mirror Question

1.  What Mirrors Do

Why do mirrors reflect left-right, but not up-down? Suppose we have a card with the letters

printed on it (as viewed from the front of the card). If we are going to view this card in a mirror we need to turn it so the front of the card faces the mirror. What we see in the mirror will then be the same as what we would see if you could view the printed letters from the back of the card (e.g., by holding it up to the light.)

But what we see will clearly depend on how we turned the card "over". If we rotated it about the vertical axis we will see

i.e., it will be reversed left-right, but if we rotate it about the horizontal axis we will see

i.e., it will be reversed up-down. This applies both to what we see in the mirror and what we see through the back of the card. In fact, we can dispense with the mirror altogether and just use a transparent plate with an image on it. We're free to rotate the plate about any axis (parallel to the plate) we wish in order to view the image from the other side. The axis of image-reversal will correspond to the axis of rotation we choose.

Of course when looking through a mirror at, say, our living room, we don't physically rotate the room. Instead, we re-orient ourselves, looking first at the room (the reference image), and then turning to look at the room's image in the mirror. To execute the turn we choose an axis of rotation which is usually vertical, resulting in a left- right image reversal. On the other hand, if we look at the room and then rotate about our horizontal axis to look at the mirror, the image we see will be reversed up-down relative to what we saw directly (because we are now standing on our heads).

There's actually an extensive literature on the question of "what mirrors do", and it has been discussed from many different points of view. It's generally accepted that the question is ambiguous because the entities (visual images) and operations (reversals) to which it refers are both inherently interpretative and of a higher conceptual order than the simple concept of a mirror. We can say without ambiguity that a mirror reflects incident rays of light, and the angle of reflection equals the angle of incidence, because the concepts of rays and angles are of the same order as mirrors. However, the notions of "visual image" and "reversal" are of a higher order, and their precise meanings are a matter of interpretation.

For example, a "visual image" may be regarded as a two-dimensional entity (which, in a purely geometric-optical sense, it is). In this sense the "effect" of a mirror can be defined as the mapping it gives between a 2D visual image viewed directly and the "same" 2D image viewed through a mirror. In these terms, the "reversal" seemingly effected by a mirror is really just a consequence of the rotation performed by the viewer as he re-orients his field of vision from the direct to the reflected image. These two fields are necessarily oriented at 180 degrees from each other, but this doesn't fully constrain how the field of vision is adjusted, because the field of vision consists not only of a direction in space but also an orientation about that direction.

Thus, if I first view an image due North, and then view the same image through a mirror due South, the axis about which the image will be reversed is precisely the axis about which I rotated my field of vision as I turned from North to South. If I turned about a vertical axis (as is most likely) the image will be reversed left-to-right, but if I turned about a horizontal axis (by standing on my head, for example) the image will be reversed top-to-bottom.

On the other hand, a "visual image" can also be construed as the 3D model that we psychologically associate with a particular 2D optical image. In support of this notion we can point out that our visual images actually consist of input from two eyes located at slightly different positions, so there is some justification for including "depth perception" as an inherent aspect of a "visual image". On this basis people sometimes say that the effect of a mirror is to reverse front-to-back, i.e., things that were furthest South in our 3D model of the direct view will be furthest North in our 3D model based on the reflected view.

However, although this approach seems plausible (and in fact it has been regarded by many people as the correct answer), there are several problems with it. On a purely formal level it can be argued that a visual image (singular) is properly defined relative to just a single point of view (eye), and that the human visual sense (for people with two eyes) is composed of two distinct visual images, from which we psychologically synthesize a mental image. Thus, we would argue that the 3D approach is answering a different question than the one that was asked (i.e., it's dealing with mental images rather than optical images).

More seriously, identifying the notion of "visual image" with the corresponding 3D model has a serious problem of non-uniqueness. It's well known that many optical images are ambiguous as to their 3D interpretation. For example, consider the image

Is this image convex or concave? In other words, are you looking at the top of a pyramid, or down into a triangular-shaped hole? Obviously this is just a 2D ASCII image, but there are real 3D objects and lighting conditions that present images just like this. If you look at such an object in a mirror, will it be reversed front to back? What if you interpret it as a pyramid when viewed directly, but as a hole when viewed through a mirror? In that case you would have to say the mirror did not reverse the image front to back. Nevertheless, the asterisk will appear to be on a different face, so clearly the mirror has done something. How can we characterize the effect of a mirror in a way that doesn't depend on subjective 3D interpretations?

All we can say for sure is that, in the 2D sense of pure optical images, an image is reflected about the axis around which our field of view is rotated as we turn from the direct view to the mirror. This is adequate to explain all the "reversals" that occur, including reversals of "handedness". For example, the image

will appear as some plane-rotated version of

when viewed through a mirror, but no plane-rotation will make it look exactly like the original, because one is left-handed and the other is right-handed. Thus, the notion of "handedness" doesn't require three dimensions. The change in handedness produced by mirrors is fully represented in the 2D optical approach. Furthermore, the 2D approach is absolute and unambiguous. In contrast, any 3D "front-to-back" effects that we may attribute to a mirror are necessarily based on ambiguous psychological interpretations.

2.  Reflections on The Mirror Question

When looking in your rear-view mirror, objects in front of the mirror (as seen in the image in the mirror) are reversed left and right, but not up and down. Why are left and right reversed, but up and down are not? To answer this commonly-asked question, we need to first answer the question: "Reversed relative to what?" From the context of the original question we can infer that it refers to the image in the rear-view mirror being reversed relative to the image we would see if we turned around and looked directly out the back window. If so, then the answer depends on how we would turn around. Most likely we would rotate our field of view about a vertical axis, so the image we see will be reversed laterally (left-to-right). Of course, if we turn about a horizontal axis (difficult to do in a car, but not impossible), the image we see would be reversed top-to-bottom.

Another answer that is often given to this question is that mirrors reverse neither left-to-right nor top-to-bottom, they reverse front- to-back. This is actually the answer to a slightly different question than the one asked above, but it's such a cute answer that many people can't resist giving it whenever anyone asks anything about mirror images.

The reason there are consistently conflicting answers to "the mirror question" is partly due to the fact that the question is often poorly expressed, so that it can be construed in several different ways. The ambiguity is two-fold, because, first, the question often doesn't explicitly identify the two things that are posited to be "reversals" of each other, and second, the question often doesn't define the intended sense of "left" and "right", i.e., as relative directions or as designations of "handedness".

Thus, if someone asks "Why do mirrors reverse left-right?" we could imagine that he's asking

(0) Why, as I look at a mirror, do objects that are actually on my left appear to be on my right, and vice versa?

In other words, he's assuming a fixed set of relative spatial directions based on his current orientation as he looks at the mirror, and he's asking how the directions of the actual objects compare with the directions of their reflected images. Of course, on this basis we're forced to conclude that the premise of the question is totally erroneous, because it's obvious that objects to the left of the viewer appear to the his left in the mirror. Thus, if we assume this interpretation we have the fun of telling him that he's so stupid, even the premise of his question is wrong, i.e., he's asking for an explanation of why something occurs when in fact no such thing occurs! Hah! It's always deeply satisfying when we can slam someone like this, thereby demonstrating the clear superiority of our thought processes.

However, when answering questions - especially informally-posed questions in a non-adversarial context - there is a certain class imperative to at least consider the possibility that the question has a valid basis, and to seek a construal of the question that is consistent with such a basis. For example, in the case of "the mirror question" we must ask ourselves whether there is any sense in which mirrors could be said to effect a left-right reversal. Given how often "the mirror question" is asked by sincere people, it is perhaps not surprising to find that there is a way of construing the "left-right reversal" premise such that it isn't totally idiotic. In fact, there are two such ways, both of which assume the "reversal" in the mirror is relative to the image that would appear if the same objects were viewed directly.

First, if some asks "why do mirrors reverse left-right?", it's possible to interpret the question in terms of left-right 'handedness', i.e., the chirality of real or apparent objects in real or imagined space. From this standpoint we would map the question to something like

(1) My friend Wally is right-handed, but when I see him reflected in a mirror, he appears to be left-handed. What gives?

This is a perfectly valid observation, and it's worth noting that imaginary-Wally is left-handed regardless of how we orient the mirror, the real Wally, or ourselves. Even if we arrange things so that imaginary-Wally appears upside down in the mirror, or so that his left hand is on our right side, he will still appear to be left-handed. This is because we're not using the words "left" and "right" here as relative directions, we're using them as designations of left and right-handed chirality of the viewed objects (real and imagined). When the question is interpreted as something like (1), the answer is that the imaginary "objects" contained in the fictitious space on the "other side" of the mirror are symmetrically reflected vis-à-vis the actual objects about the plane surface of the mirror.

Consequently we have a parity reversal that switches the 'handedness' of all the imaginary objects relative to their real counterparts. Thus the "left-right" handedness reversal of apparent objects in the mirror relative to the actual objects is a real effect on imaginary objects, i.e., a reversal of parity of all "objects" in the imaginary space "behind" the mirror. It isn't quite as much fun to give this answer as to give the "your-premise-is-wrong" answer, because here we have to admit that there is at least some rational basis for the question. However, it's still kind of fun, because we can phrase the answer so that it comes out sounding like "The left-right [handedness] reversal you've observed is actually the result of a front-back [directional] reversal. Hah!" Thus, although we can't make the questioner sound like a complete idiot, we can still make him sound very confused indeed.

Paraphrases (0) and (1) represent the two "fun" interpretations, but in order to present them plausibly it was necessary to truncate the question relative to how it is normally presented. Almost invariably when someone asks "the mirror question" he asks "Why do mirrors reverse left-right" and then adds the phrase "rather than up-down?" Hmmm...

In paraphrase (1) we assumed the term "left-right" referred to handedness (chirality), but it's hard to maintain that assumption if "left-right" is contrasted with "up-down", because the alternative to a left-right handedness reversal is not an up-down handedness reversal, but simply no handedness reversal at all. So if someone contrasts left-right with up-down, we need to consider the possibility that they are referring to left and right not as designations of chirality but as relative directions in the plane of their visual images. This suggests that we should map their question to something like

(2)  If I look in the rear view mirror of my car, the image I see is typically reversed left-to-right relative to what I would see if I looked directly out the back window. (For example, the license plates read backwards in the mirror.) But surely a plane mirror is symmetrical about all directions in the plane, so why do I see backward images rather than upside-down images? In other words, why is there a left-right reversal rather than an up-down reversal, or even some diagonal reversal?

Note the similarity between this and the question posed at the start of this note. The answer to this question clearly has to do with the axis of rotation of our field of vision. When the person turns his field of vision from the mirror to the back window he is turning about some axis, and the relation between the two visual images depends on that axis. If, as is most likely, he turns his head about a vertical axis, then the image he sees out the back window will indeed be reversed left-to-right relative to the image he saw in the mirror. In other words, things that were on his left are now on his right, and vice versa. However, if he rotated his field of vision about, say, a horizontal axis (difficult but not impossible in a car) the two visual images at his retina would be related to each other by being "flipped" about a horizontal line, i.e., the images would be upside-down relative to each other. In general, the direct and reflected visual images are "flipped" relative to each other about a line parallel to the viewer's axis of rotation.

(Needless to say, our driver has probably looked directly out the rear window enough times that he can imagine how it will look even without turning, but the point is that when he talks about image reversals in the mirror he means relative to the image he would see if he turned around in some specific way, even though he may never have cogitated on the fact that his preferred choice of physical rotation axis is what determines the axis of reversal of the mirror image.)

Notice that although none of the above answers is based on "social expectations", they do involve consideration not only of "what mirrors do" but of what we do when we look in a mirror. In both cases (0) and (1), if we say mirrors "really" reverse front-to-back, we base this claim on the observer's (mis)interpretation of the visual image coming from the flat surface of the mirror as if he was looking into a three- dimensional region of space, and making inferences about the depth or chirality of imaginary objects (although case (0) is somewhat problematic considering that both the real and the reflected object may be in "front" of us, even without imaginary "depth" inferences). In case (2) our answer is based on the raw visual images, without any interpretation, but those images are understood to be functions of the observer's field of vision and relative directions, which change as he turns (or imagines turning) from the direct to the corresponding reflected image. Thus, none of these construals of the question allows us to avoid dealing with the observer as an active element in our description.

Without the observer, the only answer we could give to the question "What do mirrors do?" is that mirrors reflect rays of light symmetrically about the normal to the surface at the point of incidence, but this clearly is not responsive to a question about perceived image reversal. Furthermore, there's no valid reason to shy away from phenomena that involve the observer in some essential way. There was such a prejudice among physicists at one time, but quantum mechanics has taught us that physics can't always clearly separate the measurement process from the thing being measured, nor the observer from the observed.

As for which of our two non-idiot interpretations is more likely to be correct, I think the fact that people almost invariably contrast left- right with up-down when asking the question clearly implies that they have in mind something like (2) rather than (1), and certainly rather than (0).

3.  A Mirror to Physics

Although to penetrate into the intimate mysteries of nature and thence to learn the true causes of phenomena is not allowed to us, nevertheless it can happen that a certain fictive hypothesis may suffice for explaining many phenomena.

                                                                                        Leonhard Euler, 1748

Question: "What does that sign say?"

 Answer: "It doesn't say anything, you have to read it."

                                                         Traditional

Why does the image of an object appears reversed left-to-right rather than top-to-bottom when viewed in a mirror. By implication, the "reversal" in question is relative to how the object appears when viewed directly. The answer is simply that an image viewed through a mirror appears reversed about the axis around which the viewer rotated his field of sight in turning from the direct to the reflected image. Since we ordinarily rotate our field of sight about a vertical axis, mirror images usually appear reversed left-to-right. (For a fuller explanation, see What Mirrors Do.)

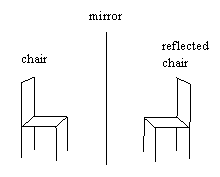
Sometimes, however, we come across a completely different "explanation" of "what mirrors do", the idea being that mirrors actually reverse things "front-to-back", as illustrated by a drawing like this:

The most interesting thing about this "explanation" is that it's clearly based on a counter-factual premise. The "chair" shown on the right side of this drawing does not exist. What really exists are reflected rays of light bearing a particular relationship to the direct rays of light from the chair. The corresponding images, which are 2D projections of those families of light rays for a particular observer, appear reversed about the axis of the observer's rotation. Nevertheless, the counter-factual explanation based on the fictive hypothesis of an imaginary chair with imaginary 3D properties appeals strongly to many people. It's actually given as "the answer", often citing an "explanation" given in one of Isaac Asimov's books.

This is a nice example of a "fictive hypothesis" that is quite successful at explaining things - up to a point. If we are standing next to the real chair we can deduce how the reflected image will appear from various points of view by *imagining* another chair in the fictitious "space" on the other side of the mirror, with the understanding that all "objects" in that "space" are reversed front-to-back, i.e. symmetrical with the real objects about the plane surface of the mirror. Of course, there's a point at which this fictive hypothesis ceases to be useful. For example, if we try to walk over to the reflected chair and sit down we quickly discover the limitations of conceptualizing reflected images as 3D objects.

The reason this counter-factual description seems so natural is that we are accustomed to dealing with our psychological constructions rather than with the primary sense perceptions on which those constructions are based. We normally presume a fairly reliable isomorphism between our perceptions and the associated mental constructs, but mirrors are somewhat unusual in that they present us with sense perceptions that we intentionally construe in a counter-factual way. A mirror is designed to simulate the sense impressions of things that really aren't "there". Notice that mirrors are among the few objects on which we almost never focus our eyes. We don't look at mirrors, we look in mirrors, with our focal lengths adjusted into the fictitious space on the "other side".

In addition to the natural tendency to deal with our mental constructs rather than our direct perceptions, the counter-factual explanation of what mirrors "do" is motivated partly by the traditional desire of physicists to separate the observer from the phenomenon. The original question asks what mirrors "do", and we tend to think this should be definable without reference to what the observer does (e.g., rotating his field of sight). However, a question about the appearance of images can only be properly answered by considering not only what mirrors "do", but also what we do when we look in mirrors. If we remove the observer from consideration, we can no longer deal with images and appearances (which is what the question asks about), because an image implies a point of view and an orientation. Without these concepts we can't really address the question at all. Oddly, many of the popular “answers” to the mirror question fail to even acknowledge the basic observation that prompts the question (reflected text appearing backwards but not upside-down), and never addresses the correlation between the observer's axis of rotation and the resulting appearance of the reflected image.

Overall, reactions to “the mirror question” nicely illustrate two problematical features of our thought processes: (1) the tension between our imaginary psychological models and our direct perceptions, and (2) our tendency to separate the observer from the phenomenon.

Return to MathPages Main Menu