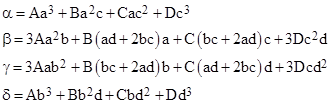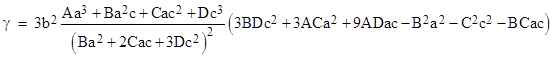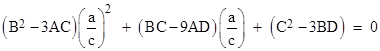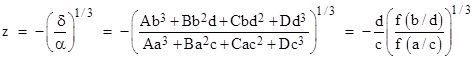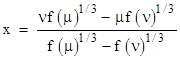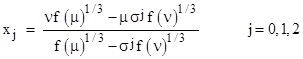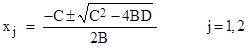On The Solution of the Cubic Equation

The discovery by Ferro, Tartaglia, and Cardano of an exact algebraic expression for the roots of a cubic equation around 1500 has sometimes been cited as a significant event in the emergence of modern scientific thought, because it was (supposedly) one of the first instances in which European scholars surpassed the knowledge of the ancient Greeks. Prior to 1500, most scholars viewed themselves as simply re-discovering the knowledge of “the ancients”, but the ancients had (apparently) never known the solution of the cubic, so this discovery gave Europeans a new sense of confidence and importance. Of course, it isn’t quite accurate to say that, prior to the cubic solution, nothing new had been discovered since ancient times. Medieval scholars actually did make (admittedly slow) progress in many areas. Moreover, Arabic mathematicians had given geometrical methods of solving cubics as early as the 9th century. For that matter, the failure of the ancient Greeks themselves to annunciate the algebraic solution of the cubic was probably due as much to a lack of interest in algebra as to inability. (After all, the problem of duplicating the cube is algebraically trivial – simply take the cube root of 2 – but it was the geometrical construction of this magnitude that interested the Greeks.) Nevertheless, it seems undeniable that European mathematicians and scientists began around 1500 to self-consciously strive to make new discoveries, and thereafter devoted much less attention to the ancient texts.

As an aside, we need hardly mention that the solution of the cubic was not the only watershed event occurring around the year 1500. Gutenberg initiated mass printing with movable type by around 1450. Columbus sailed to the new world in 1492. Copernicus first developed his heliocentric model of the solar system around 1512. Luther initiated the Protestant Reformation in 1517. Similar confluences of watershed events around the years 500 BC, 0, 500 AD, 1000 AD, and 2000 AD have led some people to speculate about a 500-year periodicity in the development of civilization.

The path that led Ferro to work out the algebraic solution of the cubic is not known, because he kept the solution a secret so that he could use it in professional challenge matches, which were apparently the customary way of choosing professors at that time. It isn’t too difficult to devise methods of solution, but it’s surprising that one of the most straight-forward methods doesn’t seem to have been followed (which we can infer from the fact that it leads to a formally different expression for the result). Given an arbitrary cubic equation

we can make a general linear fractional substitution

to arrive at the transformed cubic

with the coefficients

Notice that in order to set α = 0 or δ = 0 we would require a/c or b/d (respectively) to be a root of the original cubic. Hence we cannot gain on the solution by setting those coefficients to zero. However, we can easily find the value of d that makes β = 0, namely

Inserting this into the expression for γ gives

Thus we can set γ = 0 by setting the right-hand quadratic to zero and solving for the ratio a/c. The quadratic is

Given the value of a/c, we can substitute into (4) to give the ration d/b. It’s worth noting that the above quadratic shows the three conditions, corresponding to the vanishing of one of the three coefficients, that lead to a degenerate cubic. For example, with A=B=3 and C=1 the original cubic is (x+1)³ and all three of the coefficients of this quadratic vanish. The discriminant of this quadratic is

This is also (three times) the discriminant of the original cubic.

Now, by choosing the coefficients a,b,c,d so as to make β = γ = 0, as described above, we can then easily solve equation (3) for z, to give

Letting μ and ν denote the ratios a/c and b/d respectively, we can insert this expression for z back into the linear fractional transformation and simplify to give the following expression for the roots of the cubic f(x) = Ax³ + Bx² + Cx + D

where the ratios μ = a/c and ν = b/d are given by the formulas

and θ is the discriminant defined previously. It might seem as if this gives only two roots, since there are only two distinct values of μ, and there is a unique value of ν for any given μ. However, the expression for x contains cube roots of (in general) complex numbers, and the three roots of the cubic polynomial arise from the different cube roots. Thus the three roots can be written as

where σ is a primitive cube root of 1, e.g., σ = (−1+√−3)/2. It may not be obvious, but the same expression also gives the roots of quadratic and linear equations. In the case of a quadratic equation we have A=0 and hence θ = 3B²(4BD−C²), which results in

In this case we have f(μ) = f(ν) = (4BD−C²)/B, so the expression for the roots reduces to

With j = 0 this is indeterminate, but with j = 1 and 2 it gives the two roots of the quadratic

For a linear equation we also have B=0, so x₁ is infinite, but x₂ gives the root −D/C of the linear equation (at a removable singularity).

Return to MathPages Main Menu