The Phase Effect of Acceleration

As discussed in another note, the space and time coordinates of two point-like particles P₁ and P₂ on the x axis, each undergoing constant proper accelerated such that they maintain a constant absolute separation, can be expressed parametrically in terms of their respective proper times τ₁ and τ₂ (referenced to the coordinate time t at which they are both at rest) as

where the origin of the x,t coordinate system coincides with the pivot event of the acceleration. Let P₁ denote the particle closest to the origin, and let both particles be accelerating away from the origin in the positive x direction.

The particles share a common instantaneous locus of inertial simultaneity continuously throughout the acceleration, and these loci are rays through the origin, so the events on the two worldlines that are mutually simultaneous satisfy t₁/x₁ = t₂/x₂, which implies

and therefore τ₁/x₁(0) = τ₂/x₂(0). As a result, even though the particles maintain a fixed spatial separation along their mutual locus of simultaneity, a phase shift is introduced between them, i.e., the lapses of proper time are unequal, in proportion to their spatial distances from the pivot event.

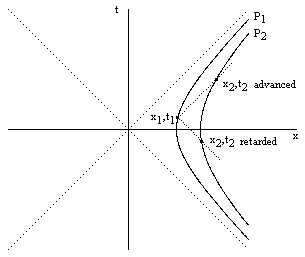
Of course, in order for two particles to undergo Born acceleration, it's necessary for their individual accelerations to be precisely coordinated at space-like separated points, and this type of coordination does not usually occur naturally (at least not on the level of macroscopic objects). In general, two physically linked particles subjected to an external force will not maintain a common locus of inertial simultaneity (on which their spatial separation is invariant), so the correspondence between the proper times on these two worldlines is ambiguous. However, as described in Section 3.6, it's possible to places the proper times along two arbitrary worldlines into a range of correspondences, whose boundaries are given by mapping from one worldline to the other along advanced and retarded lightlines. For a given point x₁,t₁ on the worldline of P₁, let x₂,t₂ denote the coordinates of a point on the worldline of P₂ that is lightlike separated from x₁,t₁, as illustrated in the figure below.

Obviously there are exactly two points on the worldline of P₂ that satisfy the stated conditions, namely, the points on the future and past light cones of x₁,t₁. These points satisfy the relations

Squaring both sides and re-arranging terms, we get

Now we can substitute the parametric expressions for x_j and t_j in terms of t_j and simplify to give

Since cosh is an even function, the sign of its argument is indeterminate, and the two possible choices give the advanced and retarded points on P₂. Solving for τ₂ in terms of τ₁, we arrive at

Incidentally, by re-arranging the terms of the original relation prior to squaring both sides, and then repeating this derivation (for both the advanced and retarded points), we arrive at the equivalent expression

and hence also

These equivalencies rely on the trigonometric identities

In any case, we see that both the boundaries of the range of potentially simultaneous τ₂ values for a give τ₂ progress in the same ratio as their distances from the origin (just as for the correspondence based on their common inertial simultaneity). In other words, we have

This was derived based on uniform proper Born acceleration, but the discussion in “Twin Times” suggests that the invariant region of "mutual present" is meaningful for any two worldlines in arbitrary motion, and it's likely that the phase shift due to acceleration of two physically linked point particles from equilibrium at rest in one frame to equilibrium at rest in another would be similar.

It's interesting to consider the consequences of the hypothesis that two physically linked point particles intrinsically resist mutual phase shifts by a force of the form

for some parameter λ of the motion of the combined particles. Take λ = τ₁, and the force is

Letting μ = x₂(0) − x₁(0) denote the rest length of the interval from P₁ to P₂, and recalling that x₁(0) = 1/a₁ where a₁ is the proper acceleration of P₁, the expression for the resistive force is simply

The parameter μ, representing the equilibrium size of the interval with respect to the co-moving rest frame, is invariant, whereas the acceleration "a" of the combined particles with respect to the x,t coordinates is related to a₁ by a = a₁(1−v²)^1/2, so the force required to effect an acceleration "a" on the combined particles with velocity v is

Obviously if we identify the invariant parameter μ with the rest mass of the combined configuration, this force is identical to the relativistic "force of inertia". It's difficult to assess the viability of this idea, because the physical dimensions of the elementary particles are not well established. Needless to say, we aren't concerned here with the Compton wavelength, and even less the de Broglie wavelength of a particle, because those are characteristics of the fields associated with particles, rather than of the particles themselves. Also, they are inversely (rather than directly) proportional to the mass. The inertia of the "bare particle" ought to be related to the actual diameter of the particle itself, which we may take to be twice the radius at which the potential observed in α-particle scattering experiments begins to deviate significantly from a Coulomb potential. On this basis, the experimental evidence indicates that a proton's radius is about (9)10⁻¹⁵ meters, and the inertial mass of a proton is (1.67)10⁻²⁷ kg, implying that the conversion from radius to mass is m = 2κr where κ = (9.29)10⁻¹⁴ kg/meter. If we assume that the proportionality between phase change and resistive force is the same for all particles (which, of course, need not be the case), then this would imply that the radius of the electron, whose mass is (9.11)10⁻³¹, should be (9.82)10⁻¹⁸. The experimental evidence to date, based on scattering experiments, indicates that the radius of the electron must be less than 10⁻¹⁶. Hence, the resolution of the data is not sufficient to either confirm or refute the hypothesis.

Coincidentally, the value of κ inferred from the mass and radius of a proton happens to be quite close to another physical constant with the same units, namely,

where m_p and m_e are the rest masses of the proton and electron, c is the speed of light, α is the fine structure constant, and h is Planck's constant. Another way of saying this is

where d_p is the diameter of the proton, and d_e is the hypothesized diameter of the electron.

Return to MathPages Main Menu