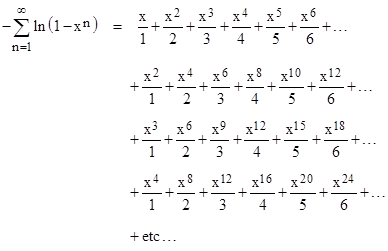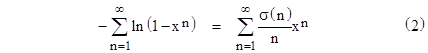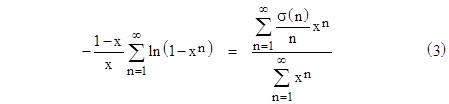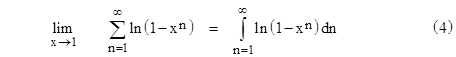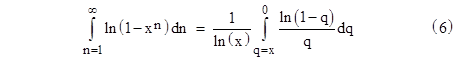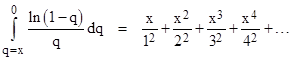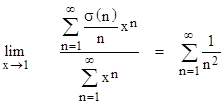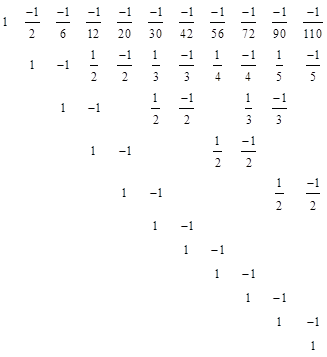Average of σ(n)/n

The sum of all the proper divisors of n is usually denoted by σ(n). For example, the divisors of 6 are 1, 2, 3, and 6, so we have σ(6) = 1+2+3+6 = 12. It’s interesting that the asymptotic average value of σ(n)/n is equal to the sum of the inverse squares (which of course has the value π²/6). One simple proof of this fact is by counting the lattice points in certain plane regions (c.f., Hardy and Wright), but there are some other interesting approaches as well. For example, by the Taylor series expansion of the natural log function, we have

for all |x| less than 1. Now, if we consider the sum of the natural logs of 1–x, 1–x², 1–x³, and so on, we have

Combining terms by powers of x gives the nice identity

If we divide both sides of this relation by the geometric series, i.e., the sum of xⁿ for n = 1 to infinity, we have

Notice that the right side of this equation a geometrically weighted average of all the values of σ(n)/n from n = 1 to infinity. Also, as x approaches 1, this approaches the evenly weighted average out to arbitrarily large n. This suggests that it would be interesting to evaluate the limit of the left side as x goes to 1. This turns out to be a somewhat delicate operation, because if the summation on the left side of (3) is evaluated for n = 1 to N for any fixed N, the overall quantity on the left side goes to zero as x goes to 1. However, for any fixed x less than 1, the quantity converges on a non-zero value as N goes to infinity, and these limiting values converge on a certain value as x goes to 1.

Anyway, by making x sufficiently close to 1 we can make the ratios of successive terms in the left-hand summation arbitrarily close to 1, so the summation can be approached by the integral in the limit as x goes to 1. In other words

To evaluate the integral, let's make the substitution q = xⁿ, where q goes from x to 0 as n goes from 1 to infinity. Noting that q can be written as exp(n ln(x)) we have

which gives

With these substitutions the integral becomes

Recalling the power series expansion of ln(1–q), we have the nice indefinite integral

Evaluating this from q = x to q = 0 gives

Substituting this back into equation (6), and from there back into equation (3), we arrive at the expression for the evenly weighted average of σ(n)/n for all integers n:

Since the ratio of –(1–x) to ln(x) goes to 1 as x approaches 1, and the numerators inside the parentheses also go to 1, we have the result

which shows, as expected, that the average value of σ(n)/n for all integers is z(2) = π²/6. This approach is certainly much less economical than the simple lattice-point derivation presented in Hardy and Wright, but it does provide the opportunity to relate some common power series expansions to arithmetic functions. For example, from the expansions of (1 – 1/x) ln(1–xⁿ) we see that the ratio σ(n)/n equals the sum of the numbers in the first n columns of the following array:

This is related to the interesting fact that the series expansion of the left side of (3) is

where the coefficient of x^k is σ(k)/k – σ(k–1)/(k–1). This converges for all x less than 1, whereas for x = 1 the partial sums are just the successive values of σ(k)/k, so it never converges. Nevertheless, the limit of the convergent values as x approaches 1 is π²/6.

Return to MathPages Main Menu