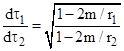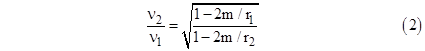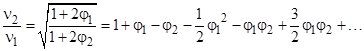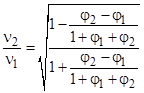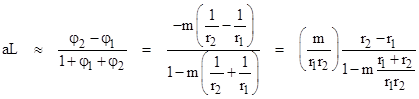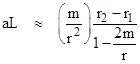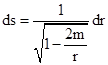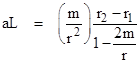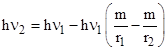Frequency and Energy

In his paper "On the Electrodynamics of Moving Bodies" Einstein derived the exact relativistic equation for the Doppler shift in the frequency of a "light complex"

where ν is the frequency with respect to the emitter and ν′ is the frequency with respect to the receiver moving away from the emitter at the speed v (in units with c = 1).  (His use of the term "light complex" rather than "light wave" was more significant than may have been apparent to his contemporaries - unless they had also studied the accompanying paper "On a Heuristic Point of View Concerning the Production and Transformation of Light" appearing in the same volume of Annalen der Physik.)  A few pages further on he derived the exact equation for the energy of the same light complex with respect to the two different inertial frames

and then remarks

It is noteworthy that the energy and the frequency of a light complex vary with the observer's state of motion according to the same law.

The significance of this fact becomes clear in the "Heuristic" paper, in which Einstein deduces another "noteworthy" fact, namely, that "monochromatic radiation of low density behaves thermodynamically as if it consisted of mutually independent energy quanta of magnitude (Rβν/N)", where R denotes the universal gas constant, N the number of quanta in one gram-equivalent (Avogadro's number), and β = 4.866 ´ 10^-11 is a constant parameter that had previously been defined by Planck.  For any light complex, one gram-equivalent corresponds to a fixed amount of energy (by the equivalence E = mc²), so the quantity Rβ/N is a universal constant, known today as Planck's constant h.  Hence Einstein was asserting that a complex of monochromatic light of frequency ν and total energy equivalent to one gram behaves as if it consists of N individual quanta (subsequently termed "photons"), each of energy E = hν.  In this assertion he was not merely suggesting that the emission and absorption events behaved as if the transmissions were comprised of discrete packets of energy, but that the transmissions themselves behaved like discrete packets of energy.

With this observation, Einstein essentially "invented" the concept of a photon, although it was many years before enough experimental evidence had accumulated for most physicists to take the idea seriously.  In fact, as late as 1913, Planck considered it necessary in recommending Einstein for membership in the Prussian Academy to apologize for it:

...there is not one among the great problems [of modern physics] to which Einstein has not made a remarkable contribution.  That he may have sometimes missed the target in some of his speculations, as, for example, in his hypothesis of the light quanta, cannot really be held too much against him, for it is not possible to introduce really new ideas - even in the exact sciences - without taking risks.

However, by 1921, after the experimental work of Millikan and others, the importance of Einstein's "hypothesis of the light quanta" had become clear enough for it to be cited as the grounds for his Nobel prize.  (Contrary to the popular conception, the technological advance to which Einstein made his greatest contribution was not the atomic bomb, but rather television, based on the photo-electric effect.  His ideas on stimulated emission of light also led directly to the invention of lasers, and so indirectly to CD players, fiber-optic communications, and so on.)  The idea that what had been regarded as waves might behave in some respects as if it consisted of discrete particles led de Broglie to consider whether entities that had been regarded as particles might behave in some respect as if they were waves.  From these insights the whole structure of quantum mechanics was developed very quickly during the 1920's.

Nevertheless, Einstein continued to regard the notion of light quanta as a heuristic, and he continued for the rest of his life trying to clarify the true nature of light (being, as he was, dissatisfied with the quantum theory as a final foundation for physics.)  The subject re-appeared throughout his later work.  For example, the first proposal for an empirical test of his general theory of relativity involves the relationship between the frequency and the energy of a "light complex".  The equivalence principle implies that a signal emitted from a stationary location in a gravitational field and received at some "higher" stationary location (i.e., a point of greater gravitational potential) will be redshifted at the point of reception.

To see why this is so, imagine two identical elevator cars, one stationary in a uniform gravitational field characterized by a constant acceleration "a" at every point, and the other in empty space (free of gravitational fields) accelerating "upward" with constant acceleration "a". 

According to the equivalence principle all observable physical phenomena inside these two cars should be identical.  In the case of the car accelerating in empty space, suppose a light signal of frequency ν₁ is emitted from the bottom of the car and subsequently received at the top of the car. Letting L denote the height of the car, and choosing units so that c = 1, the time between emission and absorption of the signal is approximately Δt = L (assuming the car moves only a small fraction of its length in the time required for the signal to traverse the distance), and therefore the top of the car at the reception event is moving away from the bottom of the car at the corresponding emission event with the relative speed v = aΔt ≈ aL.  It follows that the received frequency ν₂ will be Doppler-shifted by the ratio

Now, according to the equivalence principle, we must expect to see this same frequency shift for a light signal going from the bottom to the top of the stationary car in the uniform gravitational field.  However, the fact that the emission and absorption points are stationary compels us to place another interpretation on this frequency shift.  In the case of the accelerating car in empty space we understood that each successive wave crest had to travel a greater distance, so the intervals between their arrival times naturally increased.  In the case of the stationary car in a gravitational field, each wave crest travels precisely the same distance under exactly the same conditions (noting that the field is stationary as well).  Thus we cannot sensibly attribute the frequency shift to a progressive increase in the transit times of the wave crests.  We conclude, instead, that the rates of proper time (with respect to coordinate time) at the emitter and receiver are different.

Indeed the Schwarzschild solution of the field equations of general relativity shows that the derivative of proper time with respect to coordinate time at a radial distance r from the center of a spherically symmetrical gravitational field is

where m is the gravitational radius of the field source.  Consequently the ratio of proper time rates at the radii r₁ and r₂ is

A lessor value of dτ₁ corresponding to a given dτ₂ implies that "proper time is running more slowly" at r₁ than it is at r₂, and hence a signal emitted from r₁ with proper frequency ν₁ at that location will be received at r₂ with a proportionately lower proper frequency ν₂ given by

It's customary to let φ_j denote the "potential" -m/r_j, and then expand in the small quantities φ₁ and φ₂ to give

Neglecting higher order terms, and rearranging, gives

To check for consistency between our two elevator cars, note that the gravitational frequency shift can be written as

and comparing this with equation (1) we find the corresponding quantities

The correspondence should be exact in the limit as r₂/r₁ approaches 1, so that the gravitational field approaches uniformity.  In this limit the occurrences of r₁ and r₂ in this expression (except for the difference in the numerator) can be replaced with the mean value r, leading to the expression

The acceleration "a" and length L on the left side of this equation are defined in terms of the local proper measures of time and distance.  As discussed in the section on Radial Paths in a Spherically Symmetrical Field in the book Reflections on Relativity, the second derivative of r with respect to the proper time τ is

but the radial Schwarzschild coordinate r does not represent the local measure of proper distance.  From the Schwarzschild line element for a radial interval we have

The denominator approaches a constant as r₂/r₁ approaches 1, so in this limit we have

This shows that the correspondence

is exact, in accord with the equivalence principle.

Another way of looking at the gravitational redshift is to recall that the minimum unit of electromagnetic energy with a frequency ν that can be emitted or absorbed is E = hν where h is Planck's constant.  If such a packet of energy is emitted at r₁, its energy is diminished as it rises to r₂ due to the difference in gravitational potential at these two radii.  Hence the energy of the packet absorbed at r₂ is less than the energy of the packet emitted at r₁, so the frequency must be proportionately less.  Noting that m/r represents the potential energy per unit mass (energy) for an object at a distance r from a gravitating body of mass m, we see that the energy of the packet at r₂ is

Therefore we have

in agreement with equation (3).  This is really just a consistency demonstration, showing that it is consistent to regard the frequency of a given packet of light as strictly proportional to the energy.  Likewise the transformation equations for frequency and energy show this same consistency. 

It's interesting that the two equations most famously associated with Einstein both assert equivalencies involving energy, E = c²m and E = hν, related by the two fundamental constants c² and h.  Of course, the latter equation is really an assertion about the partitioning of energy, since it refers to the elemental unit of energy of a given frequency.  Now, from one point of view, even if we grant that energy is discretized, there is no apriori reason to expect that the energy of a light complex of a given frequency should be partitioned into discrete packets whose number is inversely proportional to the frequency.  We might, for example, imagine that the elemental light packets have energy proportional to the wavelength, or to some other characteristic parameter.  However, none of these alternative assumptions would be consistent with the effects of Doppler shift and gravitational redshift described above. 

Conversely, the "notable" coincidence between the transformation law for energy and frequency is strongly suggestive of a direct correspondence, i.e., E = hν, between these two variables, even though this obviously cannot signify an equality in the same sense that E = c²m is an equality.  Arguably the only sense in which E = hν can be interpreted is as a characterization of an irreducible quanta of light, into which any arbitrary complex of monochromatic light of frequency ν can be decomposed.

Return to MathPages Main Menu