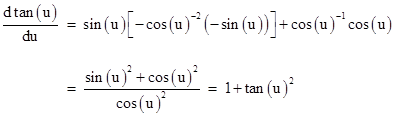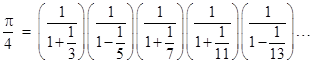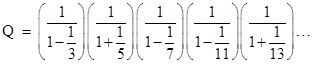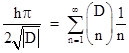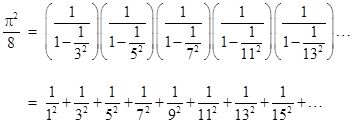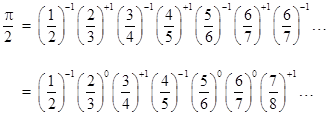How Leibniz Might Have Anticipated Euler

In 1671 James Gregory mentioned in correspondence that he had found that the inverse tangent of x equals the area under the curve of 1/(1+t²) between t = 0 and t = x.  He didn't include his derivation, but it's not too difficult to see how, with the ideas of slopes and quadratures of functions that Gregory and others were developing at the time, this result could be found.  Beginning with tan(u) = sin(u)/cos(u), we know that the slope of tan(u) versus u (in modern notation) is the derivative

Therefore, letting t denote tan(u), we have dt/du = 1 + t², and so

which leads to Gregory's result, i.e., we have

Indeed, Leibniz derived this same result independently just a few years later (around 1674).  Now, by simple division of polynomials Gregory also knew the geometric series (known to Euclid as well)

Furthermore, although this was prior to development of calculus proper by Newton and Leibniz, several people (including Fermat, Cavalieri, Pascal, etc.) had already noticed that the area under the curve tⁿ from t = 0 to x is (xⁿ⁺¹)/(n+1).  Thus Gregory had found an infinite series for the inverse tangent of x:

(Some evidence suggests that this series was actually known in India by about 1500, but the discoverer's identity is not known, nor do we know by what method the result was derived.  See Rajagopal, On Medieval Kerala Mathematics, 1986.)  A little later, thinking along  these same lines, Leibniz noted that since arctan(1) = π/4 we have the remarkable relation

It's interesting to consider what Leibniz (or Gregory) might have done with this result.  Unburdened by any concerns about re-arranging the terms of conditionally convergent series, they might well have noticed that the sum could be expressed (at least formally) as a product of geometric series in inverse primes

where each of the geometric series has either alternating signs or is strictly additive, accordingly as the prime is congruent to −1 or +1 (mod 4). (Incidentally, infinite products were certainly not unknown at this time; for example, Wallis had already found in 1655 that π/2 equals the product of 4n²/(4n²−1) for n = 1 to infinity.) Of course, each of the geometric sums in the above expression converges, and is given by 1/(1 ± 1/p), so, throwing Cauchy to the wind, we could express Leibniz's series as the infinite product

where the product is taken over all odd primes p, and the sign in the denominator is plus or minus depending on whether p is congruent to −1 or +1 modulo 4. Numerically this product converges, albeit very slowly.  Considering that Leibniz could digest the notion that 1+2+4+8+.. equals −1 based on the geometric series, it's hard to imagine him being squeamish about this product. (By the way, it follows from this expression that π would be rational if there were only finitely many primes.)

Now suppose we ask what happens if we reverse the signs in our infinite product. In other words, what if we use plus signs for primes congruent to −1 (mod 4), and minus signs for primes congruent to +1 (mod 4)?  This gives the infinite product

which, if we expand it into a sum, is

where the sign of 1/n is plus or minus accordingly as n has an even or odd number of prime divisors (counting multiplicities) congruent to 1 (mod 4). It's easy to form the conjecture based on numerical evidence that Q converges on π/2, i.e., exactly twice the former series (and product).

I don't know of any trigonometric interpretation of this series, analogous to Gregory's arctangent expansion for Leibniz's series, but we may mention Dirichlet's celebrated class number formula

where h is the class number, and the quantity in parentheses is 0 if n has a common factor with 2D, and otherwise it is the Jacobi symbol. With D = −1 this gives Leibniz's series, showing that the class number h equals 1 for D = −1. On the other hand, with D = −5 the class number is 2, and Dirichlet's formula gives

where the sign of 1/n is positive if n = 1,3,7,9 (mod 20), and negative if n = 11,13,17,19 (mod 20).

Returning to our hypothetical Leibniz and his reversal of the signs in the infinite product that formally corresponds to his famous series for π/4, notice what happens if we multiply his two results together.  We immediately have

which is the sum of the inverses of all the odd square numbers. Furthermore, since it's obvious that the sum of the inverses of the even squares is simply 1/4 times the sum of the inverses of all the squares, we have

and so S(all) = (4/3) S(odd).  Of course, this also follows simply from multiplying the product involving the odd primes by the factor 1/(1 − 1/2²) = 4/3.  Therefore, our hypothetical (and rather reckless) Leibniz has found that the sum of the inverses of all the squares is π²/6, anticipating Euler and solving the problem that defeated not only the historical Leibniz (judging from his lack of response to Oldenberg's query) but also his disciples the Bernoullis, who after much effort were able to prove only that the sum of the inverse squares converges to a value less than 2, but not to determine the value.  It remained for Euler to finally solve the problem, using means that were, if anything, even more reckless and haphazard than the reasoning above, although, to be fair, he did later provide a more rigorous argument. For more on this topic, see Factoring Zeta.

Incidentally, the infinite products of Wallis and of our hypothetical Leibniz suggest an interesting mapping between the reals in the interval 0 to 1 and the set of all real numbers. The infinite products for π/2 discussed above can be written in the form

In general, for any real number x in the range 0 to 1, let x₁, x₂, x₃,... denote the digits of x written in the base 3, and let r_i = x_i – 1. Then we define the function

Any positive real number can be represented in this way for infinitely many different values of x. For example, the two series above show that π/2 = f(x) for x = 0.02020202... and for x = 0.0120112...  It’s impossible to place any bounds on the value of f(x) based on the first k digits of x, because the remaining digits can drive any product to any value from zero to infinity.

Return to MathPages Main Menu