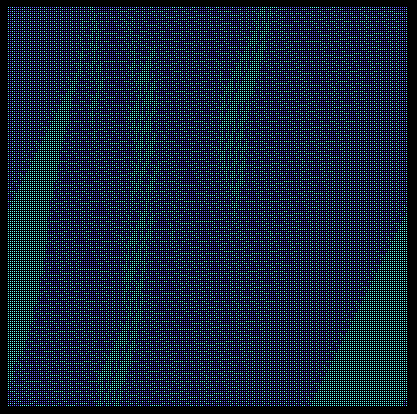|
Function 34776 |
|
|
|
Among the simplest non-trivial cellular automata are those consisting of a linear sequence of Boolean-valued cells operated on by a fixed function f of the form |
|
|
|
|
|
|
|
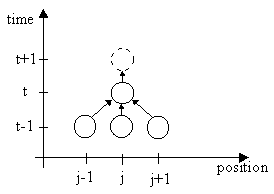
The 256 distinct functions of this form (which fall into 88 equivalence classes up to space reflection and Boolean complementation) have been extensively studied. However, it can be argued that, from a physical standpoint, this is not the most natural elementary form, if we associate the index "t" with physical time (or the negative of physical time), and if we imagine that the value of C(i,t+1) is "decided" at the time t. In order for the value of the ith cell to change, it must "know" what to change to, but by the time t+1 it has already changed; so, it must first decide at time t, and then change, bringing it to time t+1.) The above form implies that the ith cell at time t "knows" the values of the neighboring cells at the same instant. A more natural and physically plausible assumption, consistent with the finite propagation time of information, is that the ith cell at time t has knowledge of the values in the neighboring cells (and in itself) at time t-1, and it uses these past values of its neighborhood to operate on its current value to arrive at its next value. Hence we are led to consider a Boolean linear cellular automata governed by a function of the form |
|
|
|
|
|
|
|
Pictorially, the functional dependence can be illustrated as shown below. |
|
|
|
|
|
|
|
Each function of this form consists of 24 = 16 binary bits, signifying the Boolean values of C(i,t+1) for each possible set of Boolean values of the four arguments. Thus there are 216 = 65536 distinct functions of this form, falling into 17536 equivalence classes up to spatial reflection and Boolean complementation. The figure below illustrates specifies one particular function of this form. |
|
|
|
|
|
|
|
In tabular form, the function can be specified as shown below: |
|
|
|
|
|
|
|
Taking the output bits from least to most significant, this can be represented by the binary number 1000011111011000, which equals 34776 in decimal notation. If we reverse the spatial directions we get the function corresponding to 38346, whereas if we take the Boolean complement we get the function 58398. If we apply both the direction reversal and the complementation to function 34776 we get function 44118. |
|
|
|
The figure below shows the results of applying Function 34776 to a closed loop string of 200 cells, beginning with all cells on the current and previous row containing logical "0s" except for two adjacent "1s" placed in cells 49 and 50.
|
|
|
|
|
|
The dark blue cells represent logical "1"s, and the cyan cells represent logical "0"s. There is obviously an expanding envelope of "1" cells as time progresses. The above figure shows 200 iterations, with each horizontal row representing one generation of the loop. As the funnel of "1" cells expands, we begin to see an interesting feature, namely, the appearance of "0" patches within the expanding funnel of "1"s. This is shown in the figure below.
|
|
|
|
|
|
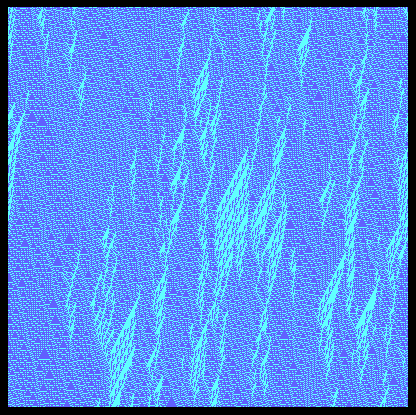
Notice that each row of cells is actually a loop, so we could regard the entire "spacetime" as the surface of a cylinder, and the funnel begins to wrap all the way around and intersect with itself. A little while later, the funnel has expanded to occupy the entire loop, but we continue to see the "wisps" of cyan patches appearing intermittantly among the chaotic pattern of dark blue triangles. If we double the size of the loop, to 400 cells, and shrink the scale so that the image fits in the same size, we get a perpetual sequence of images like the one shown below.
|
|
|
|
|
|
The seemingly chaotic background of dark blue triangles of various sizes is very similar to patterns that arise from the more common linear automata given by equation (1), but the persistent re-appearance of the superimposed cyan "wisps" is not seen in those automata. The function given by equation (2) evidently supports these two different quasi-stable mosaics, drifting slightly in opposite directions, but each of them seems to break down at various points and give way to the other. |
|
|