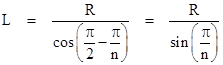Zeno's Mice and the Logarithmic Spiral

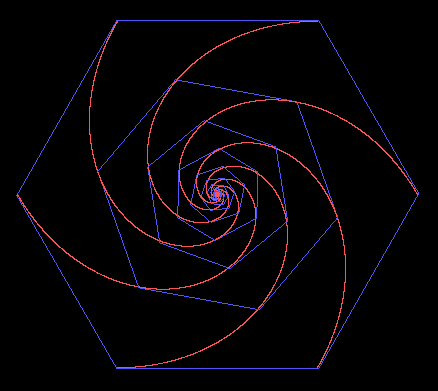
Suppose there is a mouse in each of the six corners of a regular hexagonal room, and at a given instant each mouse begins to run with a constant speed directly toward the mouse on his right. What paths will the mice follow, and what distance will they have run when they meet?  Also, what will be each mouse's total angular travel around the center of the room?

The situation is perfectly symmetrical with respect to the 6 mice, and remains so throughout the process. Thus, at each instant we have 6 mice located at the vertices of a hexagon, and they are always following the same rules about how to move, so we always have just a rescaled and rotated version of the original condition. It follows that the mice must spiral inward along similar logarithmic spirals, i.e., spirals with polar coordinates r,θ satisfying the equation ln(r) = kθ, because this is the general form of a spiral that is geometrically similar to itself on all scales. Of course, this implies that the mice just keep spiraling in a smaller and smaller circle, going infinitely many times around the center of the room, as illustrated in the figure below.

Notice that, even though a logarithmic spiral circles the center infinitely many times, the total arc length of the spiral is finite. In fact, the log spiral was the first "transcendental" curve to be "rectified". This was done by Torricelli in 1645 (before calculus was invented) using the Archimedean "method of exhaustion" for the proof. The answer is surprisingly simple, and can be seen intuitively by placing a segment of the spiral from the center C to a point P on a flat surface so the curve is tangent to the surface at P, and then "unrolling" the curve.  Since the figure is geometrically similar at each stage, it's clear that the center point C linearly approaches the flat surface as the curve unwinds.  Therefore, if we let α denote the angle that the line PC makes with the flat surface, the unwound spiral will have a length of R/cos(α), where R is the length of the segment PC.  (In other words, R is the distance from the center of the room to a corner.)

Since the spiral is tangent to the wall at the corner, we know that α is simply the angle that a line from the center of the room to a corner makes with the adjacent wall.  For a hexagonal room this angle is 60 degrees (π/3), which implies that the length of the logarithmic spiral is R/cos(π/3) = 2R.  On the other hand, if we had chosen a square room with four mice, the angle α would be 45 degrees (π/4), so the mice would have to travel a distance of

More generally, the angle between an edge of an n-sided polygon and a line from the center to a vertex of that edge is (π – 2π/n) / 2, so the general length of a logarithmic spiral inscribed within an n-sided polygon of "circumscribing radius" R is

On the other hand, as mentioned above, the total angular travel of a logarithmic spiral from any finite point to the center is infinite. Therefore, since the mice move at a constant speed, they reach the center in a finite amount of time, and hence their angular velocity must become infinite as they approach the center. The centripetal acceleration at a distance r from the center is v²/r, where v is the tangential component of the mouse's velocity, which is a constant fraction of his constant total speed. Thus his acceleration goes to infinity as r goes to zero.

This is an example what are sometimes called “supertasks”, a concept inspired by Zeno’s paradoxes of motion. In one of Zeno’s most famous examples, a faster runner can never overtake a slower runner, because he must first reach the point where the slower runner is now, by which time the slower has moved ahead by some distance, and so on, ad infinitum. Hence the faster runner must complete infinitely many intermediate tasks before actually catching the slower runner. This can be classified as a benign supertask, because its accomplishment doesn’t involve any insurmountable barrier. However, some supertasks, such as the journey of our spiraling mouse at constant speed, actually are physically impossible. The length of the mouse’s path is finite, but the angular travel about the center point is infinite, and the mouse’s acceleration goes to infinity if it maintains a constant speed along the path. This makes it easy to declare the task physically unrealizable, but what if we stipulate that the mouse varies his speed of travel in proportion to the square root of the radial distance from the center? This implies v² (the square of the tangential speed) is proportional to r, so the acceleration has a finite constant value. The mouse can still traverse the entire spiral in a finite span of time, because the path distance to the center is proportional to the radial distance, so we have

and hence the time to reach the center from a radial distance r is . But is this task really achievable? It still entails the mouse circling the center infinitely many times. Similar situations are discussed in the note on Zeno and the Paradox of Motion.

For an interesting application of this curve, see Sections 730 and 731 of James Clerk Maxwell’s Treatise on Electricity and Magnetism, which presents a discussion of general oscillatory motions. Maxwell points out that many such motions can essentially be represented by the motion of a particle subjected to two forces, one directed toward some central point with magnitude proportional to the distance from that point, and another retarding force proportional to the speed of the particle. He shows that the path of a particle subjected to such forces is a logarithmic spiral. Letting ω denote the constant angular speed, and α the characteristic angle of the spiral (i.e., the angle between a radius and a tangent), he determined that the acceleration of the particle with speed v at a distance r from the center can be decomposed into a centrally directed acceleration of magnitude μr and a retarding acceleration (opposite the direction of travel) of magnitude 2kv where

These relations can also be written in the form

Since Maxwell took ω to be constant, the oscillations persist forever, with decreasing magnitude.

It would be interesting to determine what purely central force law (if any) applied to a point particle would yield a logarithmic spiraling orbit.

Return to MathPages Main Menu