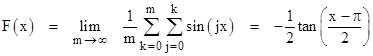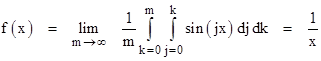|
Mean Partial Sums of Non-Convergent Series |
|
|
|
If the partial sums of an infinite series converge on a finite value the series is said to be convergent, whereas if the partial sums increase (in magnitude) without limit, the series is said to be divergent. In addition to these two kinds of series, there is another category of series - which may be called non-convergent − whose partial sums are bounded in magnitude and yet do not converge on any finite value. For example, for any real number x, consider the infinite series |
|
|
|
|
|
|
|
The individual terms are each in the range −1 to +1, and they eventually precess around the entire cycle modulo 2π, resulting in an upper bound on the partial sums. Interestingly, the mean value F(x) of all the partial sums of this series converges to give the interesting identity |
|
|
|
|
|
|
|
Thus the mean value of the partial sums of sines with uniformly distributed arguments is simply a re-scaled and shifted version of tangent. This function can also be written in the form |
|
|
|
|
|
|
|
It's interesting to consider the continuous analog of F(x), which we may define by replacing the summations with integrations as shown below |
|
|
|
|
|
|
|
Thus the function f(x) based on continuous integrals goes to zero as x increases, whereas the function F(x) based on discrete summations is periodic. These two functions do, however, approach each other for small values of x, as shown by the power series expansion of F(x) |
|
|
|
|
|
|
|
A similar construction based on the cosine instead of the sine is not as interesting, because if we consider the sum |
|
|
|
|
|
|
|
with x equal to 2nπ, the terms are all +1, and so the partial sums are unbounded. In between these divergent points the limiting function is simply the constant 1/2, basically because the cosine is an even function. By the way, it's amusing to note that the singularities at 2nπ are removable, so in this sense we can actually justify Euler's brash claim that the sum of 1 – 1 + 1 – 1 + 1 − ... is 1/2, as suggested by the geometric series 1 + x + x2 + x3 +... = 1/(1−x) with x = −1 (where the series is non-convergent). The difference is that here we have said the average of the partial sums can be analytically continued to 1/2 at x = 2π, rather than suggesting the partial sums themselves converge. Of course, by taking the average of partial sums we impose a particular order (arrangement) on the terms. For a related discussion, see Formal-Numeric Series. |
|
|