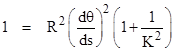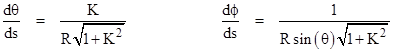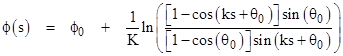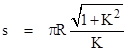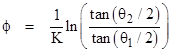Constant Headings and Rhumb Lines

The metric on the surface of a sphere of radius R in terms of the latitude and longitude angles θ and ϕ is

Note that θ = 0 at the North Pole, and θ = π/2 at the equator. At any given location if we define x,y distance coordinates with x pointing east-west and y pointing north-south, then dy = Rdθ and dx = R sin(θ) dϕ. Therefore, if we fix dy/dx = K for some constant non-zero K, we have

Dividing the metric by (ds)² and inserting dϕ/ds = (dϕ/dθ)(dθ/ds) gives

and so we have the equations of motion

which can then be integrated to give explicit expressions for θ and ϕ as a function of the path length s. The left-hand equation gives

Inserting this into the right hand equation and integrating gives

where we have put

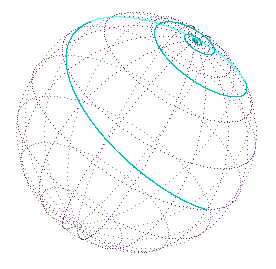
This curve on the surface of a sphere is sometimes called a loxodrome, rhumb line, or spherical helix. A path beginning on the equator and maintaining a constant heading of K=0.2 is shown in the figure below.

Curves like this were first discussed by Pedro Nunes in 1550. He is said to have believed that this curve represents the shortest distance between two points on the surface of a sphere, but considering the spiral nature of the curve near the poles, it's hard to imagine how anyone could have thought it was the shortest distance. Interestingly, a constant northwest heading (for example) will reach the pole in a finite distance, but it will circle the pole infinitely many time as it approaches. (For a similar phenomenon, see the section on “Zeno's Mice and the Logarithmic Spiral”). To see this, we can integrate the above equation for dq/ds for a rhumb line going from the North Pole (θ = 0) to the South Pole (θ = π). This gives the length of the complete rhumb line as

If K = 0 the length becomes infinite, because that represents a purely "westward" heading. On the other hand, as K approaches infinity, the heading becomes purely "northward", and the total distance between the poles is simply half the circumference, i.e., s = πR. To find the total longitude travelled by a rhumb line as it moves from the latitude θ₁ to the latitude θ₂, we can integrate the equation for dϕ/dθ to give

Obviously if either θ₁ or θ₂ equals 0 or π, the argument of the natural logarithm is either 0 or infinite, and in either case the natural log is infinite. Therefore, a rhumb line extending to either of the poles must pass through infinite longitude, i.e., it must circle the pole infinitely many times.

Return to MathPages Main Menu