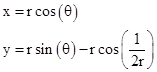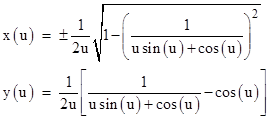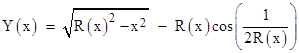Enveloping Circular Arcs

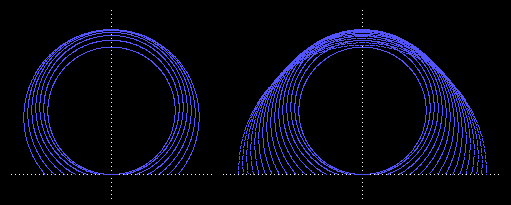
Someone asked for an equation defining the envelope of the family of circles centered on the y axis with an arc of length 1 above the x axis. To begin the construction we start with a circle of unit circumference tangent to the x axis, and then we increase the radius of the circle and lower the center point so that the length of the perimeter above the x axis remains constant, as depicted below.

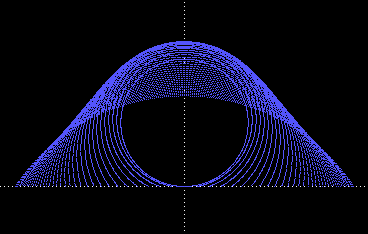
In the left hand figure each circle entirely encloses the preceding circles, and the central height has been monotonically increasing. In the right hand figure, as we continue to increase the radius of the circle and lower its central point, the top points begin to fall but the sides widen out to extend outside the previous circles.

Continuing to increase the radius and lower the center, we have

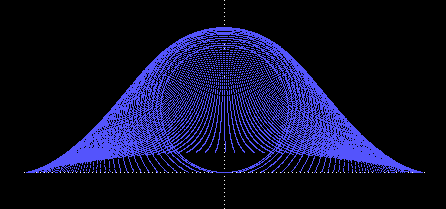
In the limit we have a complete envelope that contains this entire family of circles

Our objective is to find an explicit representation for this bell-shaped curve. By definition, the radius r of each circle is related to the vertical height y₀ of the circle's center according to

Thus, for any specified radius r, the points of the circle are given by

where θ is the angle between the positive x axis and the line from the center of the circle to the point x,y. Now, for any particular value of x, we want the maximum possible value of y. Substituting for sin(θ) = √[1 − (x/r)²] into the equation for y gives

Setting the derivative of this to zero gives the condition

This says that for any specified value of x, the value of r for the limiting circle must satisfy this equation. Solving for x and substituting into the expression for y, we arrive at an exact parametric expression for the curve representing the minimum envelope of the family of circles. For ease of typing, I'll express this in terms of the parameter u = 1/(2r)

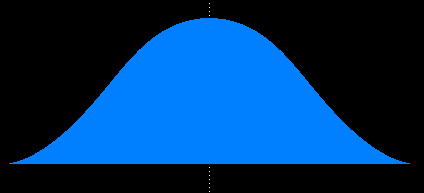
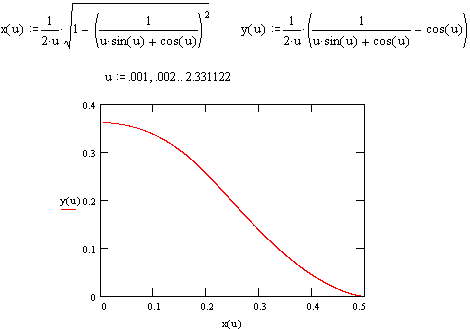
The envelope curve is governed by the circles with radii ranging from 0.214488958... to infinity, which corresponds to values of the parameter u ranging from 0 to 2.331122332... (Obviously the values of x for this curve extend only from −1/2 to +1/2, since an arc of length 1 can't reach any further.) Here is a plot of the envelope curve

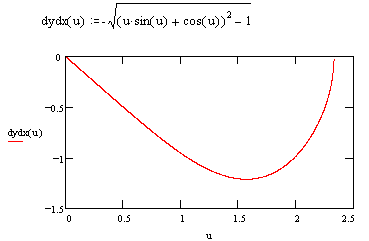
Incidentally, dividing dy/du by dx/du gives the derivative of y with respect to x:

Here's a plot of this derivative:

The maximum point occurs when this slope is zero, so the parameter u must satisfy 1 = cos(u) + u sin(u), which is transcendental, and has the solution u₀ = 2.33112237... To find the maximum height of the envelope, we can insert this u₀ back into the full parametric equation for y(u), which under these conditions reduces to simply y(u₀) = sin(u₀)/2 = 0.362305677...

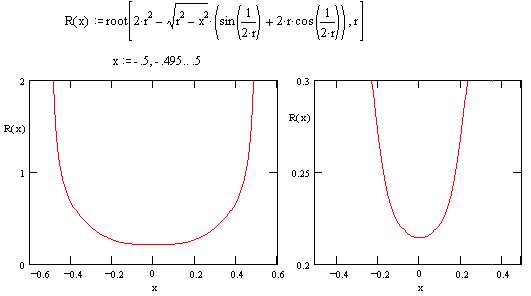
Those parametric equations are probably the simplest analytical expression for the envelope curve. On the other hand, if we choose to work numerically, we could let R(x) denote the root of equation (1) for any given x, and let Y(x) denote the corresponding value of y. Then the envelope curve can be expressed as

Evaluating Y(x) numerically, we note that the max height is Y(0) = 0.36230567..., which is achieved by a circle whose center is at y = 0.1478167... with radius r = 0.214488954... Also, the curve is closely approximated by a cosine shape, i.e., [Y(0)/2]{1 + cos(2px)}, but it's slightly fatter. The total area under the curve is 0.1921152402... (as opposed to 0.181152 for the cosine curve).

The total length of the curve can be found by integrating sqrt[dx/du)² + (dy/du)²]du from u = 0 to 2.33112237, although this is a somewhat ill-conditioned integral, so it works better with the substitution u = ln(n) and then integrating over n. The result is about 1.272305...

By the way, it might seem as if the upper part of the curve is a pure circular arc for some distance, but in fact no finite part of the curve is a circular arc, because as soon as the upper part of the circles start to drop, the circles are also expanding horizontally, which pushes out to the side while leaving the upper point unchanged. This can be seen by looking at 1/R(x) versus x:

Notice that the radius for the limiting circles is never constant, even at x = 0. Also, note that all the circles with radius less than 0.2144 are contained entirely inside the uppermost circle, so they don't contribute to the curve.

Return to MathPages Main Menu