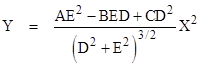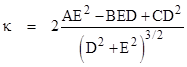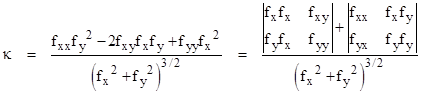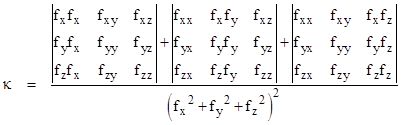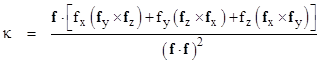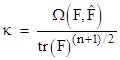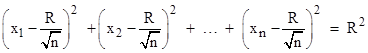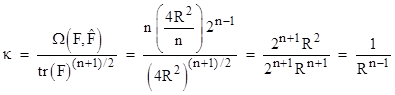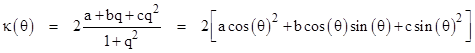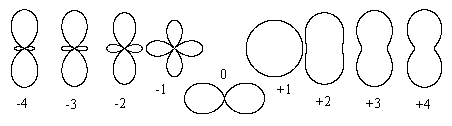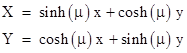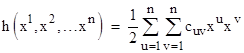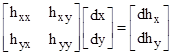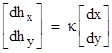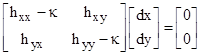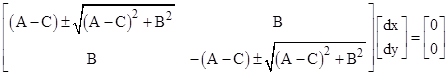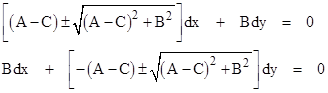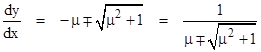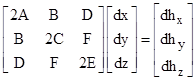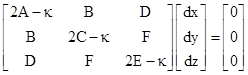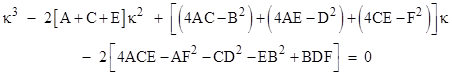The Curvatures of Hypersurfaces

A hypersurface is an n-dimensional manifold embedded in an n+1 dimensional space. Common examples of hypersurfaces include one-dimensional plane curves, and two-dimensional surfaces in three-dimensional space. In higher-dimensional hypersurfaces the concept of principal curvatures can immediately be generalized to give a nice characterization of the overall curvature of the manifold.

It's useful to begin by establishing some concepts and techniques in the simplest case of a hypersurface, namely, a plane curve. Given a one-dimensional curve embedded in two-dimensional Euclidean space, let θ(s) denote the angle of the tangent to the curve (relative to some fixed reference orientation) as a function of the path distance s along the curve. The curvature at any point on the curve is defined as the derivative dθ/ds. It follows that if a curve in the xy plane is specified by a function y = y(x) then the curvature is y"/[1 + (y')²]^3/2. If a curve is specified parametrically in terms of an arbitrary path parameter t by the functions x(t) and y(t), then the curvature can be expressed in the form (x'y" – y'x")/[(x')² + (y')²]^3/2. These are the two most commonly discussed cases.

A third way of specifying a curve in the xy plane is by means of a function f(x,y) = 0, assumed to be tangent to the origin for convenience, so we have f(0,0) = 0. The series expansion of this function up to second order about the origin is

Ax² + Bxy + Cy² + Dx + Ey  =  0

We can express this curve in terms of coordinates XY rotated about the origin through an angle α by making the substitutions X = cos(α)x + sin(α)y and Y = –sin(α)x + cos(α)y. We can force the coefficient of the linear X term in the resulting expression to zero by setting α = invtan(D/E). Inserting this value and solving for Y, we have up to second order the expression

where we have taken the negative root for the coefficient of Y. The curvature of this curve at the origin is the second derivative of this, which gives

Letting subscripts denote partial derivatives at the origin, we have

so the curvature can be expressed as a function of f and its derivatives in the form

The nice thing about this formulation is how directly it generalizes to higher dimensions. For example, consider a two-dimensional surface embedded in three-dimensional space, where the surface consists of the locus of points satisfying an equation of the form f(x,y,z) = 0. Again for convenience we shift the surface if necessary so that it is tangent to the origin at the point in question, i.e., we have f(0,0,0) = 0. By essentially the same approach as described above for one-dimensional curves, we can show that the intrinsic Gaussian curvature of this surface (the product of the two principle sectional curvatures) is given by

If we define the vector f = [f_x, f_y, f_z] then the curvature can be written in the equivalent form

Another way of expressing this curvature is in terms of a special matrix operation. Given two n´n matrices A,B, we define the scalar Ω(A,B) as the sum of each element of A times the cofactor of the corresponding element of B. In other words, we define

where b_ij denotes the minor of B_ij (viz, the determinant of the B matrix with the ith row and jth column deleted). Obviously the quantity Ω(A,A) is simply n |A|. For any given single-valued function f of the n coordinates x¹,x²,..,xⁿ in n-dimensional space let us define the two matrices F,  with the elements F_ij = f_i f_j and  = f_ij, where numerical subscript j denotes partial differentiation with respect to the coordinate x_j. On this basis the curvature of an n-1 dimensional manifold embedded in flat n-dimensional space as defined by the function f(x₁,x₂,..,x_n) = 0 is given by

where tr(A) is the trace (i.e., the sum of the diagonal elements) of A.

As an example, consider the case of an n–1 dimensional sphere embedded in n-dimensional space. In this case we have, for some choice of coordinates,

To make this surface tangent to the origin we can simply subtract  from each of the coordinates, which gives

Expanding this expression gives our function

From this we have f_i = 2R/n^1/2, f_ii = 2, f_ij = 0 for j ¹ i. Hence  is diagonal with non-zero values of 2, whereas every entry of F equals 4R²/n. Consequently each of the n diagonal entries of F has a cofactor in  equal to 2^n-1, and the other entries of F have a cofactor of zero. Also, the trace of F is 4R², so we have

This shows that the curvature of an (n-1)-dimensional sphere of radius R embedded in n-dimensional Euclidean space is 1/R^n-1, in agreement with the extrinsic curvature of a circle in the plane, and with the intrinsic (Gaussian) curvature of a 2-sphere embedded in 3D space.

In the latter case we know the intrinsic curvature is the product of the two principle sectional curvatures, which are found by evaluating the extrinsic curvatures of all the geodesic paths on the surface emanating from the origin, and determining the directions that yield the maximum and minimum curvatures. Relative to tangent normal xy coordinates we can parameterize the directions by q = y/x = tan(θ), and then the curvature of the surface defined by the local height h(x,y) = ax²+bxy+cy² above the xy plane is

To review the possible shapes of the curvature profile, without regard to rotations in the tangent plane, we can without loss of generality set b = 0 and normalize the scale by setting a² + c² = 1, and then we can consider the shapes as a function of the ratio r = a/c. Thus we have the parameterization a = r/(1+r²)^1/2 and b = 1/(1+r²)^1/2, and the shapes for various values of the ratio r are as shown below.

It's easy to show that the two principle curvatures (i.e., the min and max curvatures) are always along directions perpendicular to each other. In general, finding the principle directions amounts to solving a n´n eigenvalue problem, similar to finding the principle inertial axes of a solid. In the simple case of a 2D surface we consider transformations of the tangent xy plane of the form

where μ = invsinh[(c-a)/b]. (If b = 0 then μ = 0.)

Similarly for curved 3D subspaces of 4D Euclidean space we can evaluate the sectional curvature along any direction in the tangent space at the point in question, and determine the principle directions. The product of the sectional curvatures in these three directions is the generalized total curvature. In general for any smooth n-dimensional hypersurface embedded in n+1 dimensional Euclidean space, we can construct at any given point a system of orthogonal coordinates x^a , a = 1, 2,..., n+1 tangent and normal to the hypersurface, with the origin at the given point. In terms of these coordinates the hypersurface can be defined locally (in a sufficiently small region around the origin) by a function

Since the first n coordinates are all tangent to the surface at the origin, the first partial derivatives of h with respect to these coordinates all vanish at the origin. Hence the lowest-order terms in the power series expansion of this function are second-order, so up to second order we have

where c_uv is a symmetric array of constants for the given point and set of coordinates. The factor of 1/2 is simply for convenience, so that we can define the components of the c_uv array as the second partial derivatives

In the case of a one-dimensional hypersurface (i.e., a plane curve), the tangent axis is uniquely determined at each point, but for a two-dimensional surface in space we can obviously rotate the two tangent axes about the normal to the surface. For a three-dimensional hypersurface (embedded in four-dimensional Euclidean space) we have three degrees of rotational freedom for the tangent axes. In general we have n(n+1)/2 degrees of rotational freedom for the tangent axes to an n-dimensional hypersurface (one for each pair of axes). This implies that we can apply an arbitrary rotational transformation to the n tangent axes about the normal, which enables us to diagonalize the c_uv matrix. Once we have done this, the diagonal entries of c_uv represent the n principal curvatures of the hypersurface at the point in question. These are simply the sectional one-dimensional curvatures in the n orthogonal directions. The determinant of c_uv is the product of these principal curvatures, and the trace of c_uv is the sum of the principal curvatures. The remaining invariants of the matrix (i.e., the coefficients of the characteristic polynomial) represent all the sums of products of the principal curvatures.

Of course, the determinant, trace, etc., are all invariant under rotations, so we don't need to find the principal directions in advance. Given the c_uv matrix for any tangent-normal system of coordinates, we can determine the principal directions and curvatures simply by solving the eigenvalue problem. To illustrate, consider the simple case of a two-dimensional surface in space. At some given point on the surface we construct orthogonal xyz coordinates with the xy plane tangent to the surface. In terms of these coordinates the surface near the origin can be expressed (up to second order) by the quadratic z = h(x,y) = Ax² + Bxy + Cy², whose second partial derivatives are the components of the c_uv array

To diagonalize this array (conceptually rotating the xy axes about the z axis) we can solve the characteristic polynomial

The coefficients of the characteristic polynomial show immediately that the product of the principal curvatures (i.e., the Gaussian curvature) is 4AC–B², and the average (i.e., the mean curvature) is A+C. Solving for the individual principal curvatures gives

Conceptually this amounts to solving the eigenvalue problem of finding the directions along which the differential of the gradient vector of the surface is parallel to the displacement vector. Letting subscripts denote partial derivatives, the differential gradient vector is [dh_x,dh_y], and of course the displacement vector is [dx,dy]. The total differentials are

and these can be written in matrix form as

The components of the square array are just the second partials, c_uv. The differential gradient vector is parallel to the displacement vector if for some constant k we have

Substituting this into the previous expression and bringing the right side over to the left gives the eigenvalue problem

which can have a non-trivial solution for the displacement vector only if the determinant of the coefficient matrix vanishes, which occurs when κ is one of the two principal values (the eigenvalues). In our example the eigenvalues lead to

Substituting the partials and eigenvalues gives

This is equivalent to the two (redundant) equations

from which we get the principal directions

where μ = (A–C)/B. Note that the two alternative expressions on the right are equivalent. The two directions come from the choice of sign in either one of these expressions.

For hypersurfaces of higher dimension we can proceed in exactly the same way. For example, at any point on a three-dimensional hypersurface we can construct orthogonal coordinates w,x,y,z such that the xyz hyperplane is tangent to the surface and the w axis is normal to the surface at that point. In terms of these coordinates the surface near the origin can be expressed (up to second order) by a second-degree equation of the form

The equations for the total differentials of the gradient vector components give

Again the principal directions are those in which the displacement is parallel to the differential of the gradient vector, so we have the eigenvalue problem

Setting the determinant of the coefficient matrix to zero gives the characteristic equation

On this basis we can define the three kinds of aggregate curvatures at the given point

In general for an n-dimensional hypersurface we have n invariant curvatures K_j, j = 1, 2, .., n of the surface at each point, where K_j is defined as the average of all products of j distinct principal curvatures. We also have, at each point of the hypersurface, the n principal directions. These essentially amount to a preferred orthogonal basis for the hypersurface at each point, and we can use the union of these bases as a coordinate system on the manifold. It might seem that this conflicts with the fact that there is no smooth coordinate system covering the entirety of a surface with the topology of a sphere(for example). The explanation is that the principal directions are necessarily singular at some point on any such manifold. An example of this is a tangent plane on the surface of a perfect sphere, which has no preferred orientation at any point.

Return to MathPages Main Menu