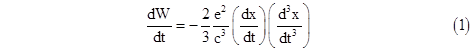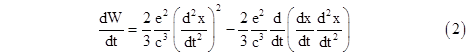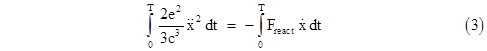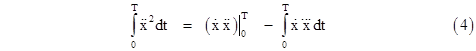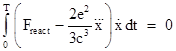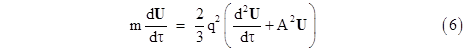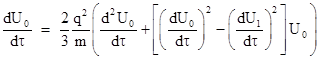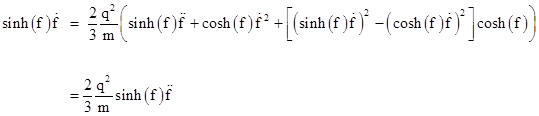Does A Uniformly Accelerating Charge Radiate?

One of the most familiar propositions of elementary classical electrodynamics is that "an accelerating charge radiates". In fact, the power (energy per time) of electromagnetic radiation emitted by a charged particle is often said to be strictly a function of the acceleration of that particle. However, if we accept the strong Equivalence Principle (i.e., the equivalence between gravity and acceleration), the simple idea that radiation is a function of acceleration becomes problematic, because in this context an object can be both stationary and accelerating. For example, a charged object at rest on the Earth's surface is stationary, and yet it's also subject to a (gravitational) acceleration of about 9.8 m/sec². It seems safe to say (and it is evidently a matter of fact) that such an object does not radiate electromagnetic energy, at least from the point of view of co-stationary observers. If it did, we would have a perpetual source of free energy. Since the upward force holding the object in place at the Earth's surface does not act through any distance, the work done by this force is zero. Therefore, no energy is being put into the object, so if the object is radiating electromagnetic energy (and assuming the internal energy of the object remains constant) we have a violation of energy conservation.

Of course, we could question the claim that no work is being done by the force holding the object in place. Indeed if we imagine a capsule in freefall, and within that capsule an object being accelerated in such a way that it maintains a constant altitude relative to the outside gravitating source, we would say, inside the capsule, we had done work on the object as we increased its velocity relative to the capsule, even though from the outside standpoint of the gravitating source the object is stationary and no work has been done on it. This is not too surprising, since work and kinetic energy are understood to be relative concepts, but it seems to lead to the puzzling conclusion that electromagnetic radiation must also be a relative concept. The familiar relativity of kinetic energy corresponds to the symmetry between different frames of reference, which is to say, we can always find a system of inertial coordinates with respect to which any given object (at a given instant) has zero kinetic energy. Our consideration of charged particles in a gravitational field seems to suggest similarly that we can always find a system of coordinates (at least locally) with respect to which a charged particle (at a given instant) does not radiate - even though the particle may be radiating at that instant with respect to some other system of coordinates.

It's also possible to question whether the equations of electrodynamics really do imply that an accelerating charge necessarily radiates. Surprisingly, this is still an open question for the classical theory. The difficulty is in knowing how to correctly account for the influence of a charged particle on itself. Remember that two electrons repel each other with a force (statically) proportional to the reciprocal of the square of the distance between them. This is traditionally understood in terms of each particle interacting with the field of the other particle. The intensity of each electron's field increases to infinity as the distance goes to zero (assuming point-like particles), so the force with which an electron is repelled increases to infinity as it approach the location of an electron - but therein lies a conceptual difficulty. According to this description, each electron is located in a place where there is an infinite force of repulsion against electrons!

We can try to deal with this in various ways. For example, we might simply declare that an electron does not interact with its own field, it interacts only with the fields of other particles. If we take this approach we must then explain why a charged particle resists changes in its state of motion more strongly than an uncharged particle of the same inertial mass. The traditional account of accelerated charges tell us that this "radiation reaction" force applied through the particle's motion supplies the energy that is radiated away in the form of electromagnetic waves. The origin of this force is usually taken to be the interaction of the particle with its own field. Thus if we declare that charged particles do not interact with their own fields we need a different explanation for radiation reaction. One well-known candidate is the Wheeler-Feynman absorber theory, according to which the excess resistance of a charged particle to changes in its state of motion is due to advanced waves emanating backwards in time from an all-encompassing array of absorbers in the future, whose waves are excited by the retarded waves emanating forwards in time from the particle.

We could also point out that although the force of repulsion on a charged particle from its own field is infinite, it is equally infinite in all directions, so the infinite forces cancel out, leaving no net force on the particle due to its own field - at least if the particle is in uniform motion. Then we can further suppose that the acceleration of a charged particle causes it to bias this singularity as it overtakes its own field, thereby incurring a net force. This same disturbance of the field results in radiation, so we can see the expected correlation between radiation and reaction. However, this approach leads to some highly non-intuitive conclusions. For one thing, the equation of motion based on this premise seems to imply that a uniformly accelerating charge does not radiate at all. (This is sometimes called hyperbolic motion, because the worldline of the particle is a hyperbola in spacetime, asymptotic to a particular pair of light rays.) Even more disquieting, we find that the equations of motion for a free charged particle possess "run-away" solutions, in which the particle rapidly accelerates toward the speed of light. In effect the particle is surfing on its own field.

Whether these solutions are realistic or not is an open question, but the predicted absence of radiation for hyperbolic motion has sometimes been cited as a way of reconciling the Equivalence Principle with the fact that a charged particle held stationary in a gravitational field (and therefore undergoing constant proper acceleration) does not radiate. For example, in Feynman's "Lectures on Gravitation" he says "we have inherited a prejudice that an accelerating charge should radiate", and then he goes on to argue that the usual formula giving the power radiated by an accelerating charge as proportional to the square of the acceleration "has led us astray" because it applies only to cyclic or bounded motions. He says the work per unit time done against the radiation reaction force for a particle moving along the x axis is actually

Thus the radiation reaction force (and therefore the radiated power) is proportional to the third derivative of position, so if the particle is undergoing constant acceleration it does not radiate (according to this formula). If this is true, why do we so commonly regard radiation as being strictly a function of acceleration? Feynman points out that (1) can be re-written in the form

where the first term is the usual expression for the radiated power. For a simple sinusoidal motion x(t) = sin(ωt) the first term is proportional to ω⁴sin(ωt)², which is positive-definite, whereas the second term is proportional to ω⁴cos(2ωt), which oscillates between positive and negative values evenly. Hence the cumulative integrated work represented by the second term over any integer number of cycles is zero, whereas the work represented by the first term increases steadily. This explains why we ordinarily neglect the second term, and take the first term as defining the radiative power, which leads us to the (erroneous) conclusion that radiation is strictly a function of the second derivative (acceleration), when in fact it is proportional to the third derivative of position. (Incidentally, if we return to the original equation (1) and apply it to our sinusoidal particle, we get power proportional to ω⁴cos(ωt)², which shows that the effect of the non-positive-definite term in the second equation is to shift the power phase by π/2.)

Despite Feynman's assurances, there is no general agreement in the literature about whether a uniformly accelerated charge radiates (in classical electrodynamics). Indeed, many people reject Feynman's conclusion as absurd. For example, in Richard Becker's "Electromagnetic Fields and Interactions" we find in paragraph 4 of Part II the claim that equation (1) is valid only for nearly periodic motions (for which all the derivatives of position are proportional to corresponding powers of the frequency), and that

Absurd results are obtained if [equation (1)] is applied to other forms of motion, such as the retardation of a free electron in a constant opposing field. In this case only the second derivative would be different from zero, and [equation (1)] would therefore predict no radiation damping at all.

The above derivation of the radiation damping is unsatisfactory, because it is not at all clear how the emitted spherical wave influences the electron's motion. In order to gain a closer understanding of the nature of this "self-reaction" it is necessary to compute the resultant force on all electron volume elements... Types of motion [such as that of the free electron] can only be treated in the light of a more precise knowledge of the structure of the electron...

Thus Becker rejects as absurd the notion that a uniformly accelerating charge experiences no radiation reaction, whereas Feynman bases his defense of the Equivalence Principle on this very notion.

Of course, above some frequency level, we know that the classical equations of electromagnetism are invalid, as shown by the "ultra-violet" catastrophe in cavity radiation. We must also account for the photo-electric effect and all the other familiar effects of quantum mechanics, which are incompatible with the simple wave conception of electromagnetic radiation. Nevertheless, even in the quantum theory of electrodynamics we find that the question of radiation reaction leads to difficulties, which to date have only been resolved in a somewhat ad hoc manner by means of re-normalization.

It's interesting to consider the result of treating electromagnetic radiation simply as the emission of classical particles at a fixed speed, ala Newton's corpuscular theory of light. Here we immediately encounter difficulties, because these corpuscles of light convey momentum, and if they are considered to be emitted discretely from the charged particle, the reaction would be an impulse, implying infinite acceleration of the emitting charged particle, albeit for an infinitely short period of time. Now, if the radiation from this particle is strictly proportional to the acceleration, we must expect the particle to radiate at an infinite rate - for an infinitesimal period of time - due to the reaction from the emission of a single corpuscle of radiation. We can argue that the total integrated amount of this radiation is finite, but the emission of each of these radiated corpuscles yields another impulse acceleration of the charged particle, resulting in still more radiation, and so on. If nothing else, this clearly illustrates the problematic nature of the dual propositions that acceleration causes radiation and that radiation causes acceleration. It's easy to see how delicately these two propositions need to be balanced in order to yield well-behaved results.

Concerning the notion that radiation is relative, it's interesting to recall the fundamental observation that led Einstein to the special theory of relativity. He began his 1905 paper on the electrodynamics of moving bodies with the words

It is well known that Maxwell's electrodynamics - as usually understood at present - when applied to moving bodies, leads to asymmetries that do not seem to be inherent in the phenomena. Take, for example, the electrodynamic interaction between a magnet and a conductor. The observable phenomena here depend only on the relative motion of conductor and magnet, whereas the customary view draws a sharp distinction between the two cases, in which either the one or the other of the two bodies is in motion. For if the magnet is in motion and the conductor is at rest, an electric field with a definite energy value results in the vicinity of the magnet that produces the current wherever parts of the conductor are located. But if the magnet is at rest while the conductor is moving, no electric field results in the vicinity of the magnet, but rather an electromotive force in the conductor, to which no energy per se corresponds, but which, assuming the same relative motion in the two cases, gives rise to electric currents of the same magnitude and the same courses as those produced by the electric forces in the former example.

In this passage the relative velocity between magnet and conductor is assumed to be constant, and no mention is made of accelerating charges or radiation, but we can surely see the possibility of a direct analogy to the case of accelerating charges. Again we find that classical electrodynamics - as usually understood at present - when applied to accelerating bodies, leads to asymmetries that do not seem to be inherent in the phenomena (especially if we accept the strong Equivalence Principle). If a charged particle undergoes oscillating accelerated motion while a distant conductor is at rest or in uniform motion, the charged particle will emit electromagnetic radiation with definite energy and momentum, and this radiation will induce slight currents in the conductor. If, on the other hand, the charged particle is at rest or in uniform motion and the distant conductor undergoes oscillating accelerated motion, no radiation emanates from the charge (according to the customary view), and yet currents appear in the conductor precisely corresponding to those in the former case, now attributed to the effects of the static electric field.

It seems reasonable to suggest that the sharp distinction which the customary view draws between these two circumstances is not justified, and that the principle of relativity (suitably qualified, of course) can be applied to the descriptions of physical effects with respect to much more general systems of reference. Indeed the strong Equivalence Principle entails precisely this, which is why Einstein viewed his theory of gravity as a generalization and extension of the principle of relativity. As early as 1911 he wrote

According to this conception once cannot speak of the absolute acceleration of a system of reference, just as in the ordinary theory of relativity one cannot speak of the absolute velocity of a system.

Oddly enough, some modern authors fail to appreciate this fundamental fact. For example, Ohanian and Ruffini write

It is tempting to give the principle of general invariance the physical interpretation that acceleration is also relative. Einstein named his theory of gravitation the theory of general relativity because he thought that (locally) the phenomena observed in a gravitational field are indistinguishable from those observed in an accelerated system of reference... However... tidal effects allow us to make an absolute distinction between the gravitational forces and the pseudo-forces found in accelerated reference frames. It is therefore false to speak of a general relativity of motion.

In reply to this, we should first point out that Einstein's theory is not the theory of general relativity, it is the general theory of relativity. The significance of this distinction should be clear. Second, the idea that tidal effects falsify the Equivalence Principle is simply incorrect, arising from a failure to recognize that the localization restriction is temporal as well as spatial. Furthermore, those who imagine that "real gravity" exists only where there is local curvature fail to consider circumstances in which a perfectly uniform stationary gravitational field over a limited region can be produced by a suitable arrangement of matter. Would they really claim that there is no true gravity in such a region because there is no local curvature? The Equivalence Principle is nothing but the spacetime version of the proposition from Riemannian geometry that a differentiable manifold is locally Euclidean.

One of the bases of our prejudice that radiation must be absolute is the notion that radiation consists of localizable entities, separate from the emitting and absorbing entities. Indeed this was one of the reasons Maxwell felt a need for a corporeal carrier or medium for radiation. He wrote

...we are unable to conceive of propagation in time, except either as the flight of a material substance through space, or as the propagation of a condition of motion or stress in a medium already existing in space... If something is transmitted from one particle to another at a distance, what is its condition after it has left the one particle and before it has reached the other?

This sort of thinking often leads people to consider a "free photon", but of course there is no such thing, at least not in our experience. A photon is necessarily both absorbed and emitted. If it weren't, we would have no experience of it. It is only the emission and absorption events that are observable, not the existence of some entity "in transit". This is closely related to the impossibility of a perfectly monochromatic wave, because in order to be perfectly monochromatic a wave can have neither a beginning nor an end. (Termination points introduce a range of frequency components.) It should also be remembered that a perfectly monochromatic wave carries no information, and therefore is not subject to any limitation on the phase velocity. We typically regard the relativistic speed limitation as applying equivalently to both information and energy, so this raises the interesting question of whether a perfectly monochromatic wave (if such a thing actually existed) would convey energy. Many of those who have studied this subject have emphasized the distinction between the case of a charge that has been uniformly accelerated for all time versus the case of a charge that has been uniformly accelerated for a long but finite time. Ultimately this connects back to the distinction between a hypothetical "free photon" (if such a thing really existed) and a real photon that is necessarily both emitted and absorbed.

Another interesting treatment of this subject is contained in A. O. Barut's book on "Electrodynamics and Classical Theory of Fields and Particles", published in 1964 and again in 1980. He begins with a heuristic derivation of the radiation reaction force based on a simple energy balance using the premise that the power (work per unit time) of the radiation is given by just the first term of equation (2). Equating the integral of this power to the integral of the radiation reaction force times the velocity we have

We now make use of the fact that

which implies

Consequently, if we choose an interval 0,T such that either the first or the second derivative is zero at both ends, then the first term on the right side vanishes, and we can substitute into equation (3) and re-arrange to give

Barut then notes that one (though not necessarily the only) solution of this equation is given by setting the integrand to zero, which implies

Hence we arrive at Feynman's equation (1), but clearly something strange is going on here. Recall that Feynman started with this relation, claiming that it was applicable to general motions, and then derived Barut's equation (3) as an approximation for periodic motion. In contrast, Barut started with equation (3), seeming to claim that it is valid for general motions, and then "heuristically" derived equation (1) as an approximation for periodic motion, precisely the opposite of Feynman's reasoning. As if this was not confusing enough, Barut then concludes by saying that "The assumption made above that d²x/dt² vanishes at t = 0 and t = T is certainly true for oscillating motion, but we expect that a result like equation (5) should be quite generally true". Unfortunately he does not elaborate on why we expect this. Everyone seems to invoke the identity (4), but there is no common agreement on how it should be interpreted, and on which terms are to be regarded as fundamental.

Much of the literature on the question of radiation from accelerating charges focuses on the Lorentz-Dirac equation of motion for a classical charged point-like particle interacting both with an external field and with its own field. This equation is the source of equation (1), but it's important to remember that it is based on classical electrodynamics of point-like particles, rather than on quantum electrodynamics, so it's physical relevance is questionable. Moreover, the internal validity of the Lorentz-Dirac equation is cast into doubt by the existence of run-away solutions (see below), which presumably are not observed - although it's interesting to consider what a run-away particle would look like. The fundamental problem is that, since this equation involves the third derivative of position, we cannot fully specify the initial conditions in terms of just position and velocity, as we can for ordinary equations of motion. The usual phase space for n particles has 6n dimensions (three position and three momentum coordinates for each particle), whereas the phase space for a charged particle under the Lorentz-Dirac equation would have 9n dimensions. Typically we regard the position and velocity (or momentum) as independent free parameters, in the sense that a physical system can be postulated to reside at any point in that phase space, and will thereafter evolve in accord with the putative laws. However, it’s less clear that position, velocity, and acceleration can be regarded as mutually independent free parameters in this same sense. The field equations of general relativity provide a good illustration of how non-linear laws imply constraints (e.g., the Bianchi identities) on the allowable initial conditions, so we are not free to specify a system at an arbitrary point in the phase space. This type of constraint applies to the Lorentz-Dirac equation as well, since it too is non-linear. However, the existence of (presumably unrealistic) run-away solutions indicates a more subtle kind of constraint on the allowable initial conditions. The allowable points in phase space must not only satisfy the instantaneous constraints, they must also (evidently) be such that they never evolve into unrealistic or singular regions of phase space. This kind of teleological constraint seems to suggest (arguably) the temporally symmetrical approach to physics.

In addition, the usual neglect of the "near" static field when dealing with the "far" radiation field is based on the assumption that the distance r from the source is sufficiently great so that the terms proportional to 1/r² are negligible compared to the terms proportional to 1/r, but the radiation reaction calculations extend all the way down to r = 0. Nevertheless, despite the dubious status and physicality of the Lorentz-Dirac equation, it's interesting to briefly review the form of this equation, and its implications. After mass re-normalization, and in terms of units such that c = 1, this equation for a particle of mass m and charge q can be written as

where U is the four-velocity, A is the four-acceleration, F is the force four-vector (with the components F^μ = F^μ_νu^μ) due to an external field F^μ_ν, and τ is the proper time along the worldline of the particle. (The scalar A² is the squared Minkowski norm of A.) The first term on the right-hand side is the Lorentz force, and the second term is the radiation reaction force. For our purposes the most interesting aspect of this equation is the fact that the radiation force vanishes if the particle's proper acceleration A is constant. In other words, the quantity in parentheses is identically zero under these conditions. To see this, we need only observe that the vanishing of the quantity in parentheses can be expressed as

The condition of constant proper acceleration implies that the squared norm of the acceleration four-vector is constant, equal to the negative of the squared norm a² of the acceleration three-vector a with respect to the particle's instantaneous co-moving inertial rest frame. Thus the radiation reaction force vanishes (for non-zero charge) if and only if the velocity four-vector satisfies the harmonic equation

The motion must be in a straight line, so we can consider just motion along the x axis with coordinate time t, in which case this equation implies

where U₀ = dt/dτ and U₁ = dx/dτ. Of course, we also have U² = U₀² – U₁² = 1. One solution of these equations is

which represents the familiar equations of "hyperbolic motion", i.e., motion with constant proper acceleration. This is the basis for the claim that a uniformly accelerated charge does not radiate, because the energy of radiation presumably comes from the work done against the radiation reaction force, which is zero for motion with constant proper acceleration - at least according to the Lorentz-Dirac equation. However, as noted previously, this equation is based on questionable assumptions, and is known to possess unphysical solutions. Perhaps the most disquieting of these are the run-away solutions. For a free charged particle with no external force, the Lorentz-Dirac equation reduces to

Focusing again on motion along the x axis, this vector equation can be split into its two component equations, the first of which is

As always, we also have the condition U₀² – U₁² = 1, and one way of automatically ensuring this condition is to set

for some arbitrary function f. Inserting these expressions into the first component equation, we have

Dividing through by sinh(f), we arrive at

Thus we have

where C = (2q²)/(3m) and the symbols k and J denote arbitrary constants. The U₁ component of (6) leads to the same conditions on f (and of course the U₂ and U₃ components are satisfied with U₂(τ) = U₃(τ) = 0), so letting K = kC, the solution of the unforced Lorentz-Dirac equation (6) for motion along the x axis can be written as

Hence the velocity of the particle with respect to the x,t coordinates is

The hyperbolic tangent is asymptotic to ±1, so depending on the sign of K the speed of the particle quickly approaches the speed of light as τ increases. These run-away (also known as "self-accelerated") solutions are widely regarded as unphysical, calling into question the validity of the Lorentz-Dirac equation of motion. It's also interesting to note that these solutions are not time-symmetric, because the constant C = (2q²)/(3m) is (presumably) positive definite. Hence the free charged particle asymptotically approaches the speed of light in the positive τ direction, whereas in the negative τ direction it approaches the fixed speed tanh(J). These solutions would be time-symmetric only if q² or m could be negative.

The strangeness of these run-away solutions has led to careful re-examinations of the premises underlying the Lorentz-Dirac equation. There are subtle issues of interpretation when trying to equate the energy of radiation with the work done on a particle, not to mention the difficulty of isolating the inertial mass m from the electromagnetic mass. (For example, when asking whether a charged particle requires the same upward force to hold it stationary in a gravitational field as does an uncharged particle of the same mass, we need to carefully consider how the charge contributes to the mass of the particle.) As a result, the Lorentz-Dirac equation does not provide a definite answer to the question of whether a uniformly accelerated charge radiates.

Return to MathPages Main Menu