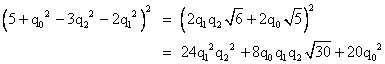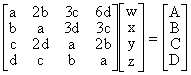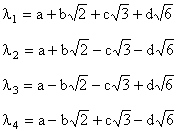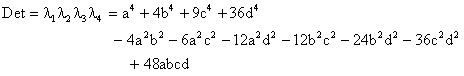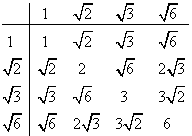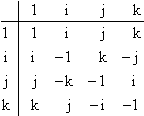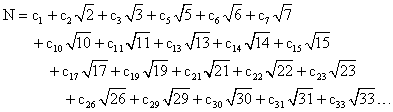Platonions

 

In Timeas, Plato proposed a "theory of everything" based on two fundamental triangles, those with edge lengths proportional to 1,1, and 1,2,.  Karl Popper speculated that Plato may have imagined that these particular triangles constitute a basis for the rational construction of all physically realizable lengths.  The square root of 2 is the diagonal of a square, and the square root of 3 is the diagonal of a cube, so (according to Popper) Plato might have hoped that these two irrationals, together with the unit 1, covered all naturally-occurring lengths in one, two, and three dimensions.  The circumference π of a unit circle is also a naturally occurring length, but Popper argued that Plato might have imagined the approximation  was exact.  Elsewhere I've discussed my reasons for thinking Popper's thesis is not very plausible, but it's still interesting to examine the field of numbers that are rational functions of Plato's basis elements.

 

It's worth noting that not only are the square roots of 2 and 3 incommensurate with the unit 1, they are also incommensurate with each other.  This was proven by Plato's friend Theaetatus, who pointed out that if there were rational numbers a,b such that  then we could square both sides to give , which contradicts the fact that  is irrational.  Of course, it is equally easy to see that the square roots of 2 and 3 do not constitute a basis for other numbers such as the square root of 5.  In other words, there do not exist rational numbers q0, q1, q2 such that

 

 

because if such rational numbers existed we could bring q0 over to the right side and square both sides to give

 

 

Re-arranging terms and squaring again gives

 

 

which is impossible because it implies the square root of 30 is rational.  Incidentally, it might seem as if this proof leaves open the possibility that the square root of 6 could be expressed in the form

 

 

but if we repeat the above procedure we get

 

 

and since the square root of 6 is not rational we must have q0 = -q1q2, so the equation reduces to

 

 

Hence this is impossible because the square roots of 2 and 3 are irrational.

 

On the other hand, given a set of numbers including all the rationals and the square roots of 2 and 3, we can also form the square root of 6 by simple multiplication, so if the set of numbers is to be closed under rational operations it must include all numbers of the form

 

 

where A,B,C,D are ordinary rational numbers.  Clearly the sum, difference, or product of any two numbers of this form is also of this form.  It only remains to consider the ratio of two such numbers.  Given any two numbers of this form, we assert that their ratio

 

 

is also of this form.  To determine the rational coefficients  w,x,y,z  we multiply through by the denominator of the left side, and collect terms according to their base, leading to the system of equations

 

 

The square matrix is contra-symmetric, i.e., its components satisfy Mi,j = M5-j,5-i.  The four eigenvalues of the system are

 

 

The determinant of the coefficient matrix is the product of the eigenvalues, i.e.,

 

 

We've already proven that the square root of 6 is not a linear combination with rational coefficients of unity and the square roots of 2 and 3, so none of the eigenvalues can vanish unless all four of the coefficients a,b,c,d are zero.  Thus division of any number of this form by any other number of this form, except for the number 0, yields another number of this form, so this set of numbers constitutes a proper field.  We'll call this particular field the Platonic Field, and elements of this field will be called platonions.  The multiplication table for the basis elements of this field is shown below

 

 

Up to rational factors, this is an example of the so-called Viergruppe (four group), which is isomorphic to the multiplication table, up to sign, of the basis elements of quaternions

 

 

We saw previously that the equation

 

 

is satisfied in rational numbers q0, q1, q2, q3 only if q0 = q1 = q2 = q3 = 0.  It follows that every number expressible in this form is uniquely expressible in this form, because given two distinct expressions for a single number, the difference between those two would vanish whereas the coefficients of the difference would not.  This fact, together with the closure of such numbers under multiplication, would have enabled Plato to see immediately that not all algebraic numbers are expressible in this form.  For example, if there existed a Platonic number equal to the square root of 5, we would have

 

 

Bringing the 5 over to the right hand side, we have a platonion, which can vanish only if each of the coefficients is zero.  The first coefficient could be made to equal zero for suitable rational values of the qi, but in order for the remaining three coefficients to vanish we must have

 

 

Multiplying these conditions together in various pairs, we get

 

 

If any two of the coefficients q1, q2, q3 are non-zero, their product can be divided out of the respective equation, leading to an impossibility, due to the irrationality of 2, 3, and 6.  On the other hand, if two of those coefficients are zero, then the prior three conditions imply that either the third is zero or else q0 must vanish.  Thus the only four possibilities are

 

 

each of which is impossible.  In fact, this analysis shows that the square root of a number N can be expressed as a platonion if and only if N is 1, 2, 3, or 6 times a rational square.

 

Since we've shown that there are no rational number q0, q1, q2, q3, q4 such that

 

 

vanishes, it follows that numbers of this form are uniquely representable.  However, the set of such numbers is obviously not closed under multiplication.  To achieve closure now that we've adjoined the square root of 5 to our set, we need to include all the products of the basis elements, so we need to consider numbers of the form

 

 

for rational coefficients.  We also want to establish uniqueness, i.e., we wish to prove that each N expressible in this form is expressible in only one way.  This is true if and only if the only expression for N = 0 is with all the coefficients equal to zero.  To prove this, assume N = 0 with some non-zero coefficients of the above expression, and bring the four right-most terms over to the other side of the equation and square both sides.  This gives

 

 

We know the quantity in parentheses on the right side is non-zero (because otherwise the quantity in parentheses on the left side would also have to be zero, and hence all the coefficients would be zero), and therefore we can divide by this platonion to give a squared platonion on the left, equated to 5.  We've already seen that this is impossible, i.e., no squared platonion is equal to 5, so it follows that our expanded set of numbers has unique representation.  Furthermore, this set supports unique division by any non-zero element, so it constitutes a field with 8 basis elements.

 

Proceeding in the same way, we could go on to show that the square root of 7 is not an element of this expanded field, and we could adjoin the square root of 7 along with the associated roots necessary to give closure under multiplication, and thereby arrive at a field with 16 basis elements.  Then we could adjoin the square root of 11, and so on, for each prime integer p.  At each stage we include basis elements consisting of the square roots of the square-free integers composed of all the primes less than or equal to p.

 

In the limit we can consider the representation with infinitely many basis elements

 

 

where the cj are rational numbers.  Thus each element is a linear combination (with rational coefficients) of the square roots of the square-free integers.  The set of numbers expressible in this form certainly contains every rational number and the square root of every rational number.  However, the uniqueness of the representation cannot be asserted, because (for example) we can express the square root of 2 as a linear combination of the square roots of the other primes, simply by a suitable choice of coefficients.  This is not possible for any finite number of basis elements, but when we allow the number of basis elements to be infinite we lose the uniqueness of the representation.  In fact, we can express every real number in this infinite form, and we can do so in infinitely many ways.

 

Return to MathPages Main Menu