|
Potential Energy, Inertia, and Quantum Coherence |
|
|
|
The bird would cease and be as other birds, |
|
But that he knows in singing not to sing. |
|
The question that he frames in all but words |
|
Is what to make of a diminished thing. |
|
Robert Frost, The Oven Bird |
|
|
|
Consider an isolated pair of electrically neutral objects, each with rest mass m, separated by a distance r. In the context of special relativity the rest mass of a set of entities is ordinarily defined as the norm of the sum of the energy-momentum vectors of the components. Hence if the two objects are initially at rest with respect to their common center of mass, the system has an overall rest mass of 2m. However, the system also entails a certain amount of potential energy due to the gravitational attraction between the two objects. If allowed to fall freely, the objects will accelerate towards each other, acquiring increasing amounts of kinetic energy. In fact, if we regarded the objects as classical point-like particles, they would acquire infinite speeds and kinetic energies as they converge (assuming zero angular momentum). Applying the previously-stated definition, we would be forced to conclude that the rest mass of the system increases to infinity. This problem did not seem acute in Newton's time, because the impact parameter for two particles could never be exactly zero, so two converging point-like particles could always be counted upon to avoid direct collision, and since the gravitational interaction was assumed to be purely conservative, stable orbits were possible. |
|
|
|
Nevertheless, the total rest mass - according to the stated definition - increases as the two objects converge. In order for mass-energy to be conserved, we need to include the potential energy in our assessment of the total mass-energy of the original configuration of the system. Then, as the objects fall together, potential energy is exchanged for kinetic energy, and the total remains constant. Two perfectly inelastic macroscopic bodies with no angular momentum would stick together when they collide, and the kinetic energy would be converted to thermal energy, raising the temperature of the objects, causing them to radiate heat. Once the combined mass has cooled back down to the temperature of the original objects, it will have radiated a certain amount of energy, so the combined rest mass will drop accordingly. Can we conclude that the final rest mass is equal to the sum of the two original rest masses? Not necessarily, because at thermal equilibrium for the same temperature, the final combined configuration might have more or less potential energy than the original configuration of two separate components. Ultimately the result depends on the energy levels of the stable bound states of different numbers of constituent particles. |
|
|
|
For a proton and an electron the dominant force of attraction is the electromagnetic force, which, like the gravitational force, has a potential proportional to 1/r. However, an accelerating electric charge (in a bounded region) radiates energy, which seems to imply that stable bound states (orbits) of electrically charged particles are impossible, because we would expect an electron orbiting around a proton to radiate energy and, as a result, spiral into the proton. The existence of stable atoms can be "explained" (to some extent) in the context of quantum mechanics by recognizing that position and momentum are conjugate variables. As an electron drops into a lower "orbit" around a nucleus it is localized in a progressively smaller spatial region, and therefore (in accord with the uncertainty relation) the momentum becomes progressively less restricted, and this momentum tends to drive the electron away from the nucleus. Thus the fundamental conjugacy of position and momentum prevents two elementary particles from occupying the same position, so there is a minimal "orbit". For a single proton and electron this minimal configuration is called the ground state of the hydrogen atom. |
|
|
|
In general an atom consists of a nucleus composed of a certain number of nucleons (protons and neutrons) surrounded by some number of electrons. The energy absorbed or released by chemical reactions corresponds to the difference between the electron binding energies of the original molecules and the electron binding energies of the products. In ordinary chemical reactions the nuclei do not change, but they may be arranged in different configurations, sharing electrons in various ways, to create different molecules. On the other hand, nuclear reactions involve reconfigurations of the nuclei themselves. The most efficient packing for nuclei occurs for a cluster of about 54 nucleons, which represents elements like iron and chromium. Roughly speaking, nuclei that contain many more nucleons than this will give off energy when they are split up (fission), and nuclei that contain many fewer nucleons than this will give off energy when they are combined (fusion). |
|
|
|
In nuclear reactions we
must account for the "strong nuclear force", which acts only over
very short characteristic distances and holds the protons in a nucleus
together, overcoming their positive electrical charges which would tend to
force them apart. In contrast with the electromagnetic and gravitational
forces, both of which have potentials proportional to 1/r, the potential of
the strong nuclear force (in its simplest form) is proportional to e−kr/r
where |
|
|
|
Since the strong nuclear force is basically attractive between every pair of nucleons, it might seem as if the more nucleons that are contained in a cluster the more strongly each of them is bound, for the simple reason that a given nucleon should be attracted N times as strongly to a cluster of N nucleon as it is to a single nucleon. However, this turns out not to be the case. The strong nuclear force exhibits a characteristic called saturation, by which the strength of attraction of a given nucleon is diminished somewhat by the capture of another nucleon. It's interesting to compare this with the electric force between charged particles. Obviously when an electron is captured by a proton the combined hydrogen atom is more or less electrically neutral, so in a sense we could regard this as a kind of "saturation", although we don't ordinarily think of it in that way. There are two kinds of electrical charges, with opposite signs, and we interpret the neutrality of a hydrogen atom as just due to the superposition and canceling out of the two fields. In contrast, the strong nuclear force apparently has only a single kind of "charge", generally attractive, so we are less inclined to regard the diminution of force as due to cancellation. We are led, instead, to the concept of saturation. |
|
|
|
The complexities of the strong nuclear force may be an indication that it is not fundamental, but composed of some simpler lower-level interactions. However, at present it is regarded as one of the four fundamental forces of nature, along with gravity, electromagnetism, and the weak nuclear force. All of these forces are usually regarded as two-body forces in the sense that they are defined strictly as pairwise interactions between particles, but there are some theoretical reasons to think that there may be fundamental three-body forces, i.e., forces that manifest themselves only in the context of three particles. Conceivably this could extend to fundamental n-body forces, but there is (presently) no empirical support for such speculations. |
|
|
|
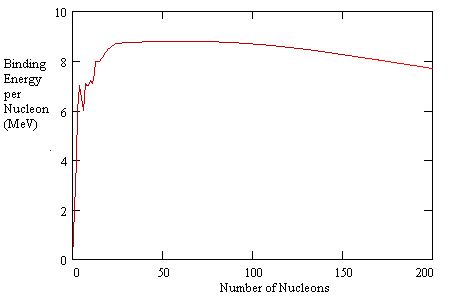
Explanations for saturation of the strong nuclear force are sometimes based on quantum "exchange forces" and sometimes based on the notion of nucleons as possessing hard shells, which is equivalent to the positing of an even more strongly repulsive force between nucleons at even shorter distances than the characteristic distance of the so-called "strong nuclear force". (The latter idea is reminiscent of the undulating force field in the Theoria Philosophiae Naturalis of Ruggiero Boscovich, (1711-1787)). Regardless of the explanation, the fact that the strong nuclear force exhibits saturation is extremely important for the structure of material objects, and for certain kinds of nuclear reactions. The binding energy per nucleon increases roughly in proportion to the number of nucleons for small configurations, but as the number of nucleons continues to increase, the binding energy per nucleon levels out, and actually decreases slightly, as shown in the plot below. |
|
|
|
|
|
|
|
The "binding energy" represents the amount of energy that would be required to pull a nucleon away from the nucleus, so the higher the binding energy, the lower the energy level of the configuration. This explains, in a general way, why fusing a small number of nucleons (such as hydrogen nuclei) together yields a release of energy, because there is an increase in binding energy, which implies that the nucleons are in a lower energy state when combined than when separated. Likewise it explains why splitting a heavy nucleus like uranium into smaller nuclei yields a release of energy, because in those cases the smaller configurations have lower energy levels per nucleon than the larger configurations. |
|
|
|
The release of energy in these nuclear reactions corresponds to a reduction in the total rest mass of the products compared with the sum of the rest masses of the reactants. In fact, the same is true for reactions involving the electromagnetic force. For example, a hydrogen atom consists of a proton and an electron, but the rest mass of a hydrogen atom (in its ground state) is slight less than the sum of the rest masses of an isolated proton and an isolated electron. Similarly the rest mass of a helium nucleus (two protons bound together by the strong nuclear force) is slightly less than twice the rest mass of an isolated proton. This is sometimes called the "mass defect", and it represents the amount of energy that was radiated away in the process of those two particles entering into a bound state of lower energy. |
|
|
|
Alternatively, the mass defect can also be described as the amount of work required to pull the two particles apart. When expressed in this way, it tends to suggest that energy (in the form of work) is added to the system by means of a force applied through a distance, and this energy then somehow becomes part of the rest masses of the individual particles. However, this interpretation raises some difficult questions concerning the localization and distribution of energy. Consider two identical particles bound together by some kind of attractive force that is a function of distance, and suppose these particles are at rest with respect to a given inertial coordinate system, and they have a combined inertial rest mass of 2(m−δ) where m is the rest mass of each individual particle. If we apply equal forces to these particles in opposite directions, we can drive them apart, moving each particle quasi-statically through the same distance. The work W done on each particle is the same, so they each gain an amount δ = W/c2 of inertial mass. Thus each particle now has acquired its individual rest mass m, and the total combined rest mass is 2m. However, if we imagine holding one particle stationary (with respect to a given inertial coordinate system) and pulling the other particle away from it, the work done on the stationary particle is zero, so all the work 2W to separate the particles has been put into the moved particle. This interpretation would seem to suggest that the inertial mass of the stationary particle is still m−δ and the inertial mass of the moved particle is m+δ. The same total amount of work has been put into the overall system in order to separate the particles, leaving them stationary at a great distance from each other, just as in the previous case, but in this case we might expect the particles to end up with unequal rest masses. |
|
|
|
To emphasize this asymmetry, we could then hold the moved particle stationary, and extract work 2W from the formerly stationary particle by allowing it to "fall" and re-enter the bound state with the other particle. If we insist that the rest mass of each particle changes strictly as a function of the work done on (or by) the particle as it is moved (or allowed to move) quasi-statically in a potential field, then we must conclude that the rest mass of the bound state is now distributed between the two particles as m−3δ and m+δ, and the particles have both been translated in space by a certain distance. (We naturally assume that space is homogeneous.) By repeating this process, it would seem we could transfer all the rest mass from one particle to the other. Since this is obviously not the case, the notion of work being converted to and from rest mass in this way is untenable. |
|
|
|
Another problematic aspect of the simple work-mass concept is that it implies that a component of the rest mass of an isolated particle represents the work done on that particle to separate it from some other particle. The problem is that we have no way of knowing from which other particle(s) it has been separated. In fact, an isolated particle is separate from every other particle in the universe, so by this interpretation its rest mass must include components representing the work done to separate it from each other particle in the universe. We might even imagine that the entire rest mass of a particle represents potential energy with respect to all the other particles. This is an intriguing idea, but since the entire rest mass of a proton is about 938 MeV and the binding energy with respect to another proton is about 2 MeV, this would imply that there are fewer than 500 protons in the universe! Of course, this neglects saturation, but if we assume each proton has a mass equal to the binding energy (per particle) with respect to a bound state of all the protons in the universe, the mass of a proton should not exceed about 9 MeV, and in fact would tend to zero as the number of particles increases (i.e., extrapolating the above figure in the direction of increasing number of nucleons). Furthermore, if there is nothing but potential energy, it isn't clear what it is the potential of. So again we conclude that the simple work-mass model is not useful. |
|
|
|
Rather than thinking of adding work to a particle to overcome another particle's attractive field, it seems more reasonable to think of the energy required to construct or establish the potential field of each particle, and to regard the inertial rest mass-energy of a particle as including the energy of the associated field(s). Because of the saturation effect, the field of two bound particles contains less energy than the sum of the field energies of two separate particles. In order to separate these particles, energy must be added to each particle to establish its full separate field. In this conceptual model, particles are seen as elemental (at least on a given scale of energies), and changes in the rest mass are due to changes in the fields associated with each configuration of particles. The field laws then determine how particles interact, and effectively govern the distribution of energy. For example, in the scenario described above, it is irrelevant which particle is held stationary and which is moved (relative to any given inertial frame), because the act of separating the particles consists of re-establishing their characteristic individual isolated fields. This requires that the energy be distributed in accord with the requirements of the field laws. In addition, the work processes themselves are more realistic, being based fundamentally on fields rather than on some undefined agency as in the work-force model. |
|
|
|
On the other hand, there are certain problematic consequences of attributing some of a particle's inertial mass to the extended fields associated with that particle. In the case of the strong nuclear force the difficulties are not so great, because the effective range of the field is on the same order as the dimension of the particle itself. However, for the long-range forces, gravity and electromagnetism, we need to ask how the inertia of the field is communicated to the source particle, and vice versa. This leads to all the well-known difficulties related to the concept of radiation reaction, and how the field of a particle affects the particle itself, if at all. (The infinities that arise in this context lead to the need for re-normalization.) Indeed it's often been suggested that inertia itself is a manifestation of the "self-reaction" of a particle with its own field. See Does a Uniformly Accelerating Charge Radiate? for more discussion of this interesting topic. |
|
|
|
Another problematical aspect of the ontological field interpretation of potential energy becomes apparent when we consider gravity, because, unlike electromagnetism and the strong nuclear force, gravity does not (as far as we know) exhibit any saturation or relaxation of the effective field as the potential is realized by acquiring other objects. Gravity cannot be "shielded". Nevertheless, a massive object can do work as it is allowed to move quasi-statically toward a large gravitating body, and this work can be radiated away from the system, so the total rest mass of the system must be reduced. According to the field interpretation, this would imply that the potential energy of the overall gravitational field had been slightly diminished by allowing the object to descend toward the gravitating body. This problem was noticed by Maxwell, and cited by him as the reason he could not explain gravity by a field theory. One might try to explain gravity by appealing to the fact that all forms of energy gravitate – a fact that Maxwell didn’t contemplate - so the work done by the descending object continues to contribute to the gravitational field of the system as long as the energy remains localized with the system. If the energy is subsequently transported or radiated away from the system in some manner, then the gravitational field of the system is diminished accordingly. However, we argue in another note that the signature of the spacetime metric – another fact unknown to Maxwell - is (in a sense) the fundamental cause of the attractiveness of gravity. |
|
|
|
For both fusion and fission of atomic nuclei, the release of energy is associated with a set of nucleons falling into a state of lower energy. In the case of fusion we have a small number of initially separate particles merging together, whereas in the case of fission we split up a large conglomeration of particles into two or more smaller groups that are packed more densely due to a reduction of the saturation effect. In other words, once the large conglomeration has been split (which just requires enough energy to escape from the local minimum), the constituent particles in each of the resulting smaller clusters fuse together more efficiently. Thus, in a sense, the release of energy in both fusion and fission reactions comes from a fusion-like process. One convenient way of visualizing this is to think of two initially resting particles with a mutual force of attraction. This initial configuration has a certain amount of relativistic mass, which equals its rest mass because the particles are not moving. If we then release the particles, they fall together, acquiring high speeds, but we can say the total relativistic mass remains constant (since no energy has gone into or out of the system). This suggests that the rest masses of the two particles (including the contributions of their bound potential energies) must be reduced as their speeds increase. At this point we can allow the particles to do work, slowing down the particles to rest, and radiate this work-energy away from the system. Once this has been done, each particle is left with its reduced rest mass (in which, again, we are including any potential energy associated with the particle), so the overall rest mass of the system has been diminished by an amount corresponding to the released energy. |
|
|
|
According to this view, the total relativistic mass of a particle remains constant as the bound particle descends (freely) into a potential field, and the effect of the descent is merely to change the distribution between rest mass and "kinetic mass" (i.e., the difference between the relativistic mass and the rest mass). It's interesting that there are two different ways of accelerating a particle. With “ordinary” macroscopic accelerations brought about by an applied external force, the rest mass of the accelerated object remains constant, and the relativistic mass increases by an amount corresponding to the work done by the applied external force. In contrast, for accelerations of elementary mutually bound particles in potential fields on a quantum scale (the same context in which an electron can be in a bound state without radiating energy), the relativistic mass of the object remains constant and the “rest mass” (including the potential energy) decreases. This implies that no work has actually been done in this acceleration. The process simply converts one type of mass-energy to another. Then the deceleration of the particle is accomplished by an external force (conductive and radiative heat dissipation) which acts like a macroscopic work process, so the rest mass remains constant and the relativistic mass decreases by an amount corresponding to the released energy. |
|
|
|
The distinction between these two kinds of processes, one of which conserves rest mass and the other relativistic mass, seems related to the different contexts in which a particle may be considered. In isolation, an accelerating force is regarded as “external”, and yet we are considering only the system consisting of the accelerated particle, and work is crossing the boundary of this system. We leave out of account the potential of the particle relative to its surroundings. On the other hand, if we consider not only the accelerated particle but also the particle(s) exerting the accelerating force, all as a bounded system, no work is passing through the boundary of the system. The accelerations that occur must then be interpreted differently in order to account for the variations in energy and mass of the constituents. This is all very reminiscent of the notion of quantum measurement and state coherence. When an entity is viewed (observed) in isolation, it’s individual wave function collapses onto one of the observable eigenvectors, whereas if we consider interactions taking place between the parts of an isolated compound system, the individual parts remain in a superposition of states, and these may interfere with each other, leading to qualitatively different outcomes than anything that could occur to the parts when viewed individually. |
|
|