Musings on Attractive Forces

O, I am out of breath in this fond chase!

The more my prayer, the lesser is my grace.

Happy is Hermia, wheresoe'er she lies;

For she hath blessed and attractive eyes.

                                                    Shakespeare

The existence of elementary attractive forces has always presented a puzzle to those who sought to conceive of physical processes in classical mechanistic terms. For example, Descartes argued that every physical interaction should be reducible to impulses between material objects, but on this basis it is difficult to conceive of how any force of attraction or cohesion can possibly exist. Indeed this was one of the early criticisms of Newton’s theory of gravitation, which seemed to posit an elementary innate force of attraction (although Newton himself declined to endorse any particular mechanism). In the 1690s Newton’s protégée Nicholas Fatio attempted to reconcile Newton’s theory with Cartesian principles by proposing a “shadow theory”, according to which all objects are subject to impulses from a universal flux in all directions, and they mutually shield each other, resulting in a net “attraction” (or more accurately a deficit of repulsion) on every body toward every other body. Many physicists of note, including (allegedly) Newton himself, said that if gravity has a classical mechanistic cause, then it would have to be a shadow theory, almost by definition. Nevertheless, very few physicists ever found Fatio’s theory plausible or appealing, partly because of the ruinous thermodynamic features, but also because it tacitly relies on the existence of cohesive bodies, so it doesn’t really eliminate the need for elementary attractive forces (unless we postulate an infinite regress of meta fluxes on all scales).

In a sense the existence of attractive forces of electromagnetism is more easily rationalized with mechanistic intuitions, because we have both positive and negative charges. Maxwell (for example) conceived of empty space as a dielectric medium capable of absorbing and releasing energy. The attraction between oppositely charged particles can be seen as arising from the energy that must be put into their surrounding fields in order to separate the particles of opposite charges. However, as Maxwell noted, this kind of explanation cannot be applied to gravitation, in which “like” particles attract each other. (See the note on Why Maxwell Couldn’t Explain Gravity.)

The modern theory of quantum electrodynamics involves quantizing Maxwell’s equations. Accordingly the forces between material objects arise from an exchange of momentum quanta. The Coulomb force between electrically charged particles is said to be mediated by photons. It is intuitively clear how the emission of a photon from one particle and the absorption of that photon by another particle can result in a repulsive force between the two particles, because we can easily imagine that the emitting particle recoils away from the receiver when it emits the photon, and the receiving particle is pushed away from the emitter when it absorbs the momentum of that photon. On the other hand, it's less obvious how an exchange of photons can result in an attractive force between two particles, such as exists between an electron and a proton. The literature contains a variety of attempts to convey an intuitive sense of how this works, from various points of view. Despite their seeming variety, they all rely (either explicitly or implicitly) on some aspect of time reversal for elementary interactions. This is inevitable (barring a shadow theory) if we are to explain in any meaningful way how momentum in one direction can be conveyed in the opposite direction. The concepts of negative energy and negative frequency are just disguised ways of referring to characteristic processes with a negative time sense.

To explore this in a simple context, it’s interesting to consider a primitive toy model of interactions. Let’s suppose that the electromagnetic force is produced by discrete momentum-carrying entities (which we will call “photons”) exchanged between particles along null space-time intervals.  In other words, if x_e, y_e, z_e, t_e are the (inertial) coordinates of the emission of a photon from one particle, and if x_a, y_a, z_a, t_a are the coordinates of the corresponding absorption events at another particle, then

This actually represents two physically distinct kinds of intervals, because we can transpose t_e and t_a.  Thus if we conceive of null intervals in a directed sense going from one given spatial location to another, there are two distinct kinds, namely, the advanced null intervals and the retarded null intervals.

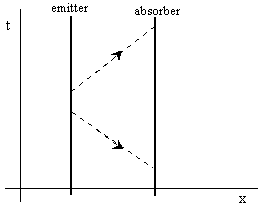
In macroscopic terms, we normally think of entities moving in the direction of increasing time, but on the level of fundamental quantum interactions, especially along null intervals, there is no justification for this asymmetry.  An individual quantum of momentum (viz., a photon) can just as well propagate along an advanced null interval as it can along a retarded null interval.  These two types of transfers are illustrated in the space-time diagram below.

We know the effect of a photon transmitted in the positive t direction (on the future null cone of the emitter) is to repel the two particles away from each other, but what is the effect of a photon transmitted in the negative t direction?  To answer this question, suppose both particles transfer a photon to the other, at the same two events on their worldlines, one propagating in the positive t direction and the other in the negative t direction as shown below.

The net effect of this is zero, i.e., there is no net transfer of momentum, so there is no net force.  The superposition of these two transfers is really a non-interaction.  Since the forward-going transfer represents a repulsive force, and it is cancelled out by the backward-going transfer, it must be the case that the latter represents an attractive force.  This is the same as saying that the momentum of a photon propagating in the negative t direction is negative, which is consistent with what we would calculate for the momentum of a massive particle going backward in time based on the definition p = d(mv)/dt.  It can also be understood intuitively by considering the time-reversed version of ejecting an object, which is not to receive a thrown object, but to capture (draw in) an object, thereby resulting in the opposite momentum transfer.

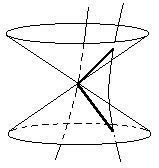
It's interesting to consider how the propensities of individual charged particles could be characterized so as to give a repulsive force between like charges and an attractive force (of equal magnitude) between unlike charges.  The worldline of every massive particle intersects with the lightcone of each event on the worldline of any other massive particle in exactly two points, as illustrated below.

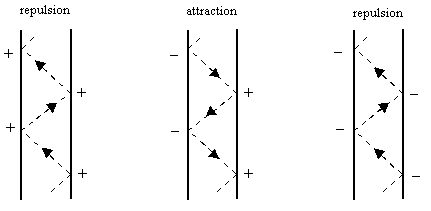
We say there is a propensity for a photon to be transferred in the positive t direction along any given null interval between the worldlines of two particles if the charges at both ends of the interval have the same sign, whereas there is a propensity for a photon to be transferred in the negative t direction along any given null interval between the worldlines of two particles if the charges at both ends of the interval have opposite signs.  This gives the three types of interactions shown below.

More generally, we could characterize each particle by a set of four numbers, representing the propensities of that particle to emit and absorb advanced and retarded photons (or any other force-mediating entity).  Let ε⁺ and ε^- denote the propensities to emit photons in the positive and negative t directions respectively, and let ρ⁺ and ρ^- denote the propensities to absorb photons from the positive and negative t directions respectively.  The product of corresponding emission and absorption propensities gives the joint propensity for the respective transfer.  (If the joint propensity is negative, the direction of the transfer is reversed.)  In terms of these parameters, the force F₁₂ between two particles P₁ and P₂ is proportional to

If negatively charged particles are characterized by

and positively-charged particles are characterized by the opposite values, i.e.,

then we have the results

On the other hand, if we wanted to construct a single class of particles, each of which is attracted to other members of the same class, we could assign the propensities

giving a net force proportional to -1 between two such particles. Interestingly, such particles would be neutral with respect to both of the preceding kinds of particles. If we represent each possible type of particle by a four-bit binary number, with 0 and 1 representing -1/2 and +1/2 respectively, then the 16 possible types fall into two sets, those that interact with themselves and those that don’t. The net interaction (multiplied by 4) for each pair of particles is shown in the tables below.

Granted that we can represent the transfer of attractive momentum in this way, is it realistic to consider photons propagating in the negative direction?  It's well known that Maxwell's equations are time-symmetrical, and permit advanced as well as retarded waves.  There has been a long history of debate on the subject of whether the advanced solutions have any physical meaning, and indeed whether they are even physically realized at all.  And if not, why not?  The standard answer is that although Maxwell's equations would permit advanced waves, such waves would only arise due to a set of coordinated boundary conditions that is extremely unlikely to spontaneously occur.  On the other hand, the absorber theory of Wheeler and Feynman showed how (at least in the context of classical electrodynamics with an opaque future) it is possible to combine both the advanced and retarded solutions into a single model that is consistent with observation.

Of course, when we talk about the exchange of quanta of momentum we are no longer working in the context of Maxwell's equations, which are strictly classical and treat the propagation of electromagnetic momentum as waves in a continuous field.  It is certainly plausible that the boundary conditions necessary to support a macroscopic coherent wave converging inward from the future has a negligible probability, but this does not at all preclude the transfer of a single quantum along an advanced null interval.  The boundary conditions necessary to support this transfer are no more complex than the boundary conditions to support a transfer along a retarded null interval.  At the level of individual quantum interactions, there is no reason to expect any asymmetry at all between these two directions.

A more serious objection can be raised against the literal interpretation of force-mediating particles with definite trajectories in space-time, because photons are not actually localized particles with persistent identities.  It's more accurate to regard them as terms in a series expansion, and since a given series can be expanded in different ways, the individual terms have no absolute significance. 

Another possible objection is that we've assumed that all interactions occur along null space-time intervals, whereas it's more conventional to represent forces in terms of virtual particles whose emission and absorption events are space-like separated.  With such intervals there is no absolute sense of forward and backward in time.  Nevertheless, it can be shown that no energy or information (outside the bounds set by the uncertainty principle) propagates at superluminal speeds.  This suggests that it should also be possible to represent the interactions in terms of effects that propagate strictly over null intervals.  This applies even to matter waves, which, as Dirac explained, propagate along null intervals as well, provided they are considered on a small enough scale.  Therefore, even the short-range nuclear force, mediated by massive particles, can also be accommodated within this framework.

Return to MathPages Main Menu