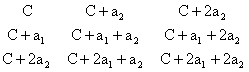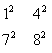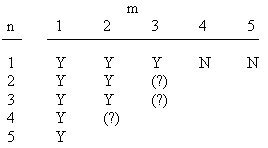|
Coherent Arrays of Squares |
|
|
|
Given a set of n real numbers a1, a2,..., an we can define an n-dimensional array A of size mn by
|
|
|
|
|
|
where C is an arbitrary constant and m is a positive integer. We'll refer to an array of this kind as coherent. If we regard the components of such array as the values of a continuous function of the indices, then the defining characteristic is that the partial derivative with respect to each index is a constant, i.e., |
|
|
|
|
|
|
|
For example, given two real numbers a1,a2 and a constant C, and taking m=3, we have a 3x3 array of the form |
|
|
|
|
|
A coherent array with n=1 is simply an arithmetic progression of length m, whereas a coherent array with m=1 is just a single constant for any n. |
|
|
|
It's interesting to consider, for various dimensions n and sizes m, whether there exist coherent arrays with those parameters whose components are all square integers. We know there are sets of three squares in arithmetic progression, but there are no four squares in arithmetic progression. Therefore, we can say that there exist coherent arrays of squares of dimension n=1 and of size m=1,2,3, but not of size m=4 or greater. |
|
|
|
If we go on to consider arrays of dimension n=2, it's easy to see that there exist coherent arrays of squares of size m=1 and 2. For example, we have the array |
|
|
|
|
|
|
|
However, it's less clear whether there exists a 2-dimensional coherent array of squares of size m=3. The existence of such an array is equivalent to the existence of a 3´3 magic square of squares. |
|
|
|
For dimension n=3 the first non-trivial case to consider is arrays of size m=2. It turns out that there do exist coherent arrays of squares with n=3,m=2, such as |
|
|
|
|
|
|
|
This array is generated by the values a1 = 2400, a2 = 4389, a3 = 8736, and C = 100. The eight components can be pictured as lying at the eight vertices of a cube. Obviously given any such array we can create another by simply multiplying each component by a fixed square. All the primitive solutions with greatest partial derivative less than 2000002 are listed in the Attachment. |
|
|
|
The next case to consider is arrays of dimension n=4 and size m=2. To search for these, we can simply take each coherent array of squares with n=3,m=2 and check to see if there is any integer a4 which, when added to each component, gives a square. None of the n=3,m=2 solutions listed in the Attachment gives a solution of this kind. So, we have another open question. It may be that no coherent array of squares of dimension n=4 and size m greater than 1 exists. |
|
|
|
The table below summarizes what is known about coherent arrays of squares of various dimensions and sizes. The symbol "Y" signifies that arrays exist, "N" signifies that they do not exist, and "(?)" means none are known but the existence has not been disproved. |
|
|
|
|
|
|
|
Obviously if no arrays exist for a given n,m, then none exist for any pair of parameters greater than or equal to n and m respectively. |
|
|