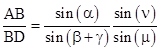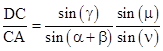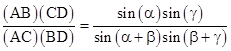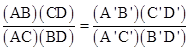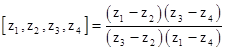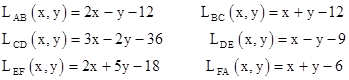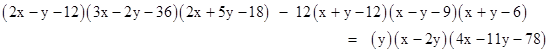Pascal's Mystic Hexagram

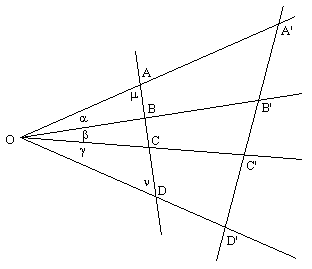
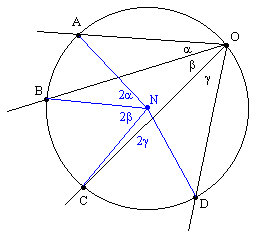
One of the first applications of modern mathematics to emerge during the Renaissance was the study of perspective for the purposes of painting and architecture. This led naturally to a consideration of projection, i.e., the mapping of images from one plane surface S to another plane surface S′ by projection from a point O. The point p on S maps to a point p′ on S′ such that O, p and p′ are colinear. Obviously the distances between points and the angles between lines are not preserved under a projective mapping, but certain properties of figures are preserved. For example, straight lines map to straight lines, and conics map to conics. In addition to these qualitative invariants, there are also quantitative invariants. Consider four points A,B,C,D on a line in S, projected from the point O to the points A′, B′, C′, D′ on a line in S′ as shown below.

Applying the law of sines to the triangles OBA and OBD, we have

The ratio of these two is

Likewise if we apply the law of sines to the triangles OCD and OCA we get

Thus if we multiply AB/BD by DC/CA the sines of m and n cancel out, and are left with

This quantity is called a cross-ratio, and we see that it depends only on the angles between the projecting rays emanating from the point O, so it has the same value if we project the four points A,B,C,D onto any other line. In other words, we have

Furthermore, since the distances between the points don't change if we change the position of the projecting point O, it follows that the cross-ratio is the same for any projection point. Also, given the positions of any three of the co-linear points A,B,C,D and the value of their cross-ratio, the position of the fourth point is fully determined.

It's worth mentioning that although we speak of "the" cross-ratio of four points, the value depends on the order in which we take the points. There are 4! = 24 possible permutations, but it's not difficult to show that, because of symmetries, there are only six distinct values of the cross-ratio, and these come in reciprocal pairs. Thus there are three real values p,q r such that the six cross-ratios for four given points are p, 1/p, q, 1/q, r, 1/r. In addition, we have the relations

All 24 permutations of A,B,C,D can be produced by combining the six possible transpositions of the points. These transpositions have the effect of cycling between pairs of values, as summarized below.

So, to define a single cross-ratio we need to specify four co-linear points (or, equivalently, four lines that intersect at a given point) in a particular order. We will use the notation [ABCD] to indicate the cross-ratio of the co-linear points A,B,C,D in that order. When referring to four lines emanating from the point O and passing through the points A,B,C,D we will designate the origin point with a subscript, as in [ABCD]_O.

Incidentally, the cross-ratio is also an important quantity in complex analysis. Given any four complex numbers z₁, z₂, z₃, z₄, the cross-ratio defined as

is invariant under arbitrary Mobius (i.e., linear fractional) transformations. This quantity is a purely real number if and only if z₁ through z₄ lie on a straight line or a circle.

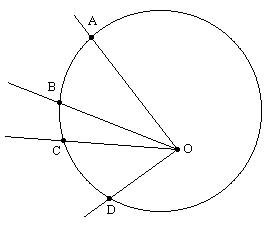
Geometrically we can define a cross-ratio either in terms of four points on a line or in terms of an origin and four arbitrary points in a plane with the origin, since these four points specify a set of four lines through the origin. For example, we could specify a cross-ratio in terms of a given origin point O and four points A,B,C D on the perimeter of a circle as shown below.

Since the points A,B,C,D are not co-linear, the cross-ratio depends on the position of the origin point O. Thus if we take the same four points but consider the lines through them emanating from a different origin located, say, on the circle itself, the cross-ratio is different, because the angles between the lines are different. However, it's easy to see that the cross-ratio for four given points on a circle is the same for an origin located anywhere on the same circle. This is illustrated in the figure below with the origin point O located at an arbitrary point on the circle.

We know from elementary geometry that if N is the center of the circle then the angle ANB is twice the angle AOB for any point O on the circle. Therefore, if the points A through D are fixed, the cross-ratio for any origin point on the circle is invariant. Furthermore, since the cross-ratio is invariant under arbitrary projections, this proposition is valid for arbitrary conics as well. In other words, given any four points on a conic (such as an ellipse, hyperbola, or parabola), the cross-ratio for the lines through those points is invariant for any origin point located anywhere on the same conic.

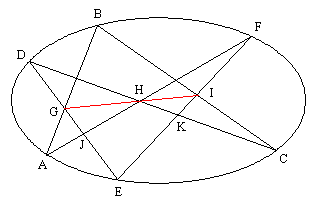
To illustrate the usefulness of these ideas, consider six points A through F placed arbitrarily on a conic, such as on an ellipse as shown below, draw the lines AB, BC, ..., EF, FA, making a hexagon.

Visually it appears that the points G, H, I at the intersections of opposite edges of this hexagon are co-linear, as indicated by the red line, but we would like to prove this. In other words, we wish to prove that the segments GH and HI really lie along a single line.

A typical proof making use of cross-ratios begins with the fact that [EKIF]_H is equal to [EKIF]_C. Now, the lines emanating from C and passing through K and I also pass through D and B respectively, so [EKIF]_C is equal to [EDBF]_C, and we can switch origin points from C to A, because they are both on the ellipse, so these cross-ratios equal [EDBF]_A. We notice that the lines emanating from A and passing through the points B and F also pass through G and J respectively, so the cross-ratio equals [EDGJ]_A. Since these points are co-linear, the cross-ratio also applies to the origin H, so it equals [EDGJ]_H. Thus we've shown that [EKIF]_H equals [EDGJ]_H. The points K and D represent the same line through H, and the points F and J represent the same line through H, so it follows that the points I and G fall on a single line through H, which was to be shown.

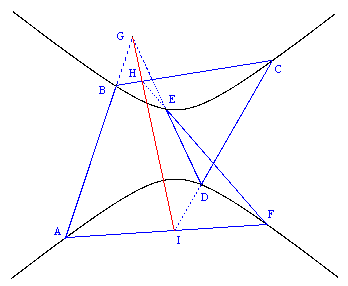
As noted previously, a conic curve is projected to a conic curve, because a projection maps curves of second degree to curves of second degree. Therefore, the above theorem applies to any hexagon inscribed in any conic. For example, if we place the vertices of a hexagon on a hyperbola we arrive at a figure as shown below.

Notice that we extend the edges of the hexagon as necessary to find the intersection points of opposite edges. We can also arrange the vertices so that the points of intersection lie entirely outside the figure, as shown for the ellipse below.

This theorem was first stated in 1640 by Blaise Pascal (1623-1662) when he was just 16 years of age. His father, Etienne, had retired from his civil service job in 1631 to devote himself to the education of Blaise and his two older sisters. At the age of 14 Pascal joined his father as a member of the group of mathematicians and scientists associated with Marin Mersenne. In addition to the Pascals, this remarkable group included (either in the weekly meetings or by correspondence) Descartes, Fermat, Gassendi, Desargues, Roberval, Beeckman, Peiresc, and Hobbes, along with extensive communications with Huygens, Torricelli, Galileo, and many others. Girard Desargues (1593-1662) originated the idea of projective geometry, and Pascal wrote that he (Pascal) owed everything he had found on the subject to the writings of Desargues. Unfortunately Desargues' brilliant innovation occurred simultaneously with the introduction of analytic geometry by Descartes, so the ideas of projective geometry were over-shadowed for nearly two hundred years. The younger Pascal was one of the few people to appreciate the power and beauty of Desargues' approach to geometry, but Pascal himself soon gave up mathematics and devoted most of the rest of his short life to theology.

Oddly enough, Pascal didn't actually present "his theorem" as a theorem, nor did he ever publish a proof of it. The only thing he ever published on the subject was a brief summary, announcing several results without proof. This was to be followed by a comprehensive treatise on conics, which Pascal apparently worked on for many years, but then abandoned. No copies have survived, so we have only the brief statements from the 1640 "Essay on Conics" (along with notes that Leibniz took when he saw a copy of Pascal's unpublished treatise). In terms of the lettering in the figure above, Pascal stated that:

If through points K,V any conic section whatever passes cutting the lines MK, MV, SK, SV in points P,O,N,Q, then the lines MS, NO, PQ will be of the same order.

Pascal carried over from Desargues the definition of an ordonnance of lines as a set of lines passing through a common point, so when he says the lines MS, NO, PQ are of the same order, he means they pass through a single point. This of course is equivalent to saying that the point of intersection of the lines NO and PQ is co-linear with the points M and S, which is the way "Pascal's Theorem" is usually expressed today.

The above statement follows two lemmas, the first of which is identical to the above statement except that it refers only to a circle rather than a general conic section. The second lemma states simply that "If through the same line several planes are passed, and are cut by another plane, all lines of intersection of these planes are of the same order as the line through which these planes pass". In other words, if a plane containing a certain line is cut by another plane, then the line of intersection of these two planes passes through the given line. (Of course, this is understood to be in the sense of projective geometry with its lines and points at infinity to cover the cases of parallel lines and planes.) Then Pascal says "On the basis of these two lemma's and several easy deductions from them, we can demonstrate" the general proposition about conics quoted above. After listing several other results, the brief essay concludes

There are many other problems and theorems, and many deductions which can be made from what has been stated above, but the lack of confidence which I have, owing to my little experience and capacity, does not allow me to go further into the subject until it has passed the examination of able men who may be willing to take this trouble. After that if someone thinks the subject worth continuing, we shall endeavor to extend it as far as God gives us the strength.

Alas these were the last words Pascal ever published on the subject.

Of course, Pascal's celebrated theorem is a generalization of Pappus' Theorem. Ironically, it can be argued that a true understanding of it comes only when viewed from the algebraic standpoint of Descartes' analytic geometry, as pointed out by Julius Plücker (1801-1868) using the fact that two algebraic plane curves of degree m and n with no common factor have mn points of intersection (counting multiplicities and points at infinity). This is called Bezout's Theorem for obscure reasons, since Bezout apparently never proved it, and the proposition had been stated and used by earlier mathematicians such as Newton. In any case, the equation of a line L(x,y) = 0 has degree 1, and the union of m lines is just the product of the equations of the individual lines, so it has degree m. Thus for both the theorem of Pappus and the theorem of Pascal the inscribing figure is a locus Q(x,y) = 0 of degree 2, and we can split the six lines into two sets of three to give the two functions L_ABL_CDL_EF and L_BCL_DEL_FA, each of degree 3. Therefore, these loci intersect with each other in nine points, six of which are on the inscribing locus and three of which are not.

Now, any linear combination of the two cubics also intersects with Q at the six given points, but in addition we can choose the coefficients (of the linear combination) so that the combined function intersects Q at a seventh point, which implies that Q has a common factor with the combination of cubics. If Q is an irreducible conic, the common factor can only be Q itself. If Q is the product of two linear factors (as in Pappus' Theorem), then we need simply note that the combination of cubics can be forced to pass through the intersection of the two factors, so the combination of degree 3 intersects with each line in four points, and therefore it must have a common factor with each of them, which again implies that the entire inscribing function Q divides some linear combination of the two cubics. Thus there must be constants α,β and a linear function L(x,y) such that

Therefore, the three zeros of the two cubics that do not lie on Q(x,y) = 0 must lie on the straight line L(x,y) = 0. This proves Pappus' and Pascal's theorems together, and immediately points to higher-order generalizations.

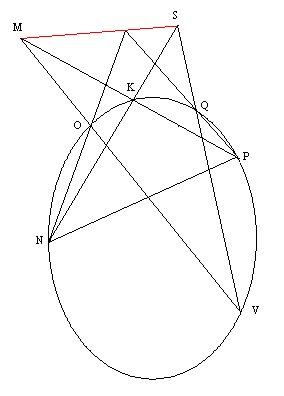
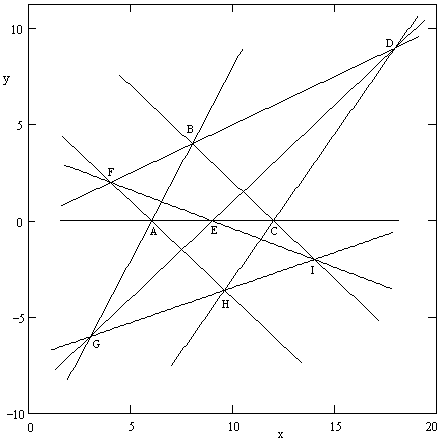
For a simple example, consider the instance of Pappus' theorem in the figure below.

Algebraically, the inscribing locus consists of the two lines y = 0 and x - 2y = 0, so it is represented by the quadratic

The edges of the hexagon ABCDEF are the lines

So, by Bezout's Theorem, we know there exist real numbers α,β and a linear function L(x,y) such that equation (1) is satisfied. We find that α = 1 and β = –12 gives

Therefore, the three points G, H, I must lie on the straight line 4x – 11y – 78 = 0.

Return to MathPages Main Menu