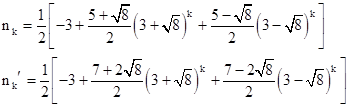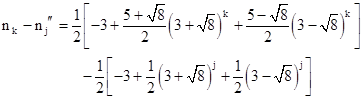A Unique Intersection Pattern for Plane Curves

As discussed in the note on Cramer's Paradox, any two algebraic plane curves of degree n intersect in exactly n² complex points (counting multiplicities and points at infinity), and each such curve is uniquely determined by a set of n(n+3)/2 general points.  The apparent paradox (for n greater than 2) is resolved by the fact that of the n² points of intersection between two curves of degree n there are only n(n+3)/2 − 1 degrees of freedom.  Thus the n² points can be partitioned into n(n+3)/2 − 1 independent points and (n−1)(n−2)/2 dependent points.  For the particular case n = 10 the 10² intersection points consist of 8² independent points and 6² dependent points, so we can imagine taking the 64 points of intersection of a pair of octics as the independent intersection points for a family of decatics, such that the 36 dependent points might be the intersection points of two sextics.  This possibility arises because with n = 10 the quantities n(n+3)/2 − 1 and (n−1)(n−2)/2 are both non-zero squares.  No other value of n satisfies this condition, so the case n = 10 is unique.

To prove uniqueness, we can solve each of the conditions

for n, which gives n = (-3 ± r)/2 and n = (3 ± s)/2 where r and s are integers such that

The Pell equation on the left has two sequences of solutions, r = 5, 23, 133, 775, etc., and r = 7, 37, 215, 1253, etc.  Each of these sequences satisfies the recurrence r_k − 6r_k−1 + r_k−2 = 0, so we can give the values of r_k as explicit functions of k, leading to the explicit expressions for the corresponding positive values of n shown below.

The other Pell equation has just a single sequence of solutions, s = 1, 3, 17, 99, etc., and again these values satisfy the recurrence s_j − 6s_j−1 + s_j−2 = 0, so we can give the corresponding values of n explicitly as

(We omit the trivial solutions n = 1 and n = 0 given by the other sign.)  It's easy to verify that the only common value of n_k (or n_k′) and n_j″ for small indices k and j is n₁ = n₂″ = 10.  For larger indices equality is ruled out by placing bounds on the difference between nk (or n_k′) and n_j″.  We have

which vanishes if and only if

The smaller root of the characteristic equation (3 minus the square root of 8) is much less than 1, so as the indices k and j increase, these terms become negligible, so we need to satisfy the approximate equality

Clearly we must have j > k, so this can be written as

The minimum magnitude of the quantity in square brackets for integer values of j−k is 2, which occurs with j−k = 1.  Thus in order to achieve equality the leading factor cannot exceed approximately 6.  The argument of this factor is 5.828..., so the only possible solution occurs with k = 1.  For any higher values of k, equality is ruled out.  This proves that the only solution is the one with k = 1 and j = 2, which gives n = 10.  By similar reasoning we can rule out equality between n_k' and n_j" for any indices k and j.

Return to MathPages Main Menu