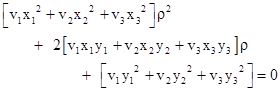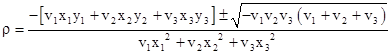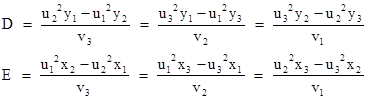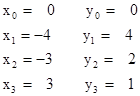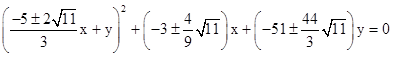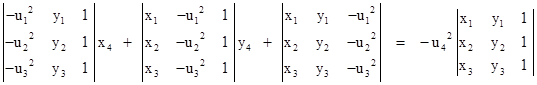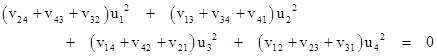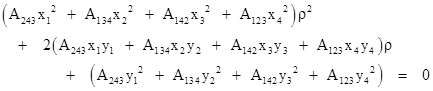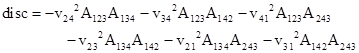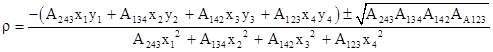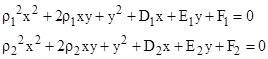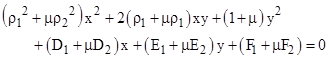Revisiting the Four-Point Parabola

A conic is a locus of points satisfying the second-degree polynomial

where x and y are orthogonal coordinates on a plane.  The conic is a parabola if and only if B² = 4AC, in which case we can define constants a,c such that A = a² and C = c² and write the equation in the form

Given four arbitrarily selected points P_j on the plane, with coordinates x_j,y_j, for j = 0,1,2,3, we can shift all the points so that P₀ lies on the origin.  The parabola through those four points then passes through the origin, so we have F = 0.  Also, since we can divide through by any of the quantities a², c², D, E (if they are non-zero) there are really only three degrees of freedom, which we can use to require that the remaining three points (P_j, j=1,2,3) satisfy the equation, so we have

Solving any two of these for D and E, and substituting into the third, we find the necessary and sufficient condition for the parameters a,c to give a parabola through these points is

Letting X and Y denote vectors with components x_i and y_i respectively, for any given set of three points, we can define the cross-product vector V = X x Y with the components

This establishes a mapping between three-point configurations (equivalent up to translations and rotations) and vectors in a three-dimensional space.  These quantities are invariant under rotations as well as translations. Also, if we divide through the equation by c² we get a quadratic in the ratio ρ = a/c. Letting u_j = ρx_j + y_j, and letting Q denote the vector with components u_j², the preceding equation can then be written as the vanishing of the dot product V∙Q = 0. Hence the necessary and sufficient condition for a and c to give a parabola through the four points is that Q must be in the same plane as X and Y.

The quadratic in ρ can also be written as

The two roots are

We can also define the one-parameter family of vectors q(σ) with components

By varying the value of σ we vary the direction of this vector. The two roots ρ are such that q(ρ) is orthogonal to V, i.e., such that q(ρ)×V = 0.  These two values correspond to the two orientations for which a normal parabola through the origin passes through all three of the points.  The equation of this parabola is

where ρ is either of the two roots of the characteristic quadratic and the values of the coefficients D and E are given by

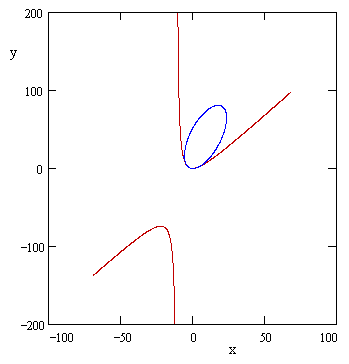
As an example, consider the four co-plane points with coordinates

The characteristic polynomial is

with the roots

From this we find the corresponding values of the D and E coefficients

Thus the two parabolas through the four given points (including the origin) have the equations

where the ± are either all plus or all minus.  Expanding the square and collecting terms, we can split the equation into rationally incomensurate parts (for rational x and y) as follows

This implies that any rational points (x,y) on the parabola must also be on each of the curves represented by the two expressions in parentheses.  By Bezout's Theorem these two curves intersect in four points, so the original four points (0,0), (-4,4), (-3,2) and (3,1) are the only rational points on the parabola.  Incidentally, the curves given by the two parenthetical expressions are an ellipse and a hyperbola respectively.  These are shown in the figure below.

We can regard the quantities ax_j + cy_j as comprising the values of a transformed variable, and since only the ratio of a/c is important we can parameterize them as a = sin(θ) and c = cos(θ).  (It follows that the parameter ρ equals tan(θ).)  Then we have the transformed variable

In terms of this variable the original equation of a parabola is

If we then define a second variable consistent with the first by means of a simple plane rotation through the angle θ, we have

Thus the original variables are given by

so we can substitute into the parabola's equation to give

The preceding discussion began with four arbitrary points on the plane and then we translated the points so as to place one of them at the origin.  This simplifies the expressions, but tends to obscure the full symmetry of the solution.  Any four points can be fit them to the general parabola equation

Letting u_j denote ρx_j + y_j we can substitute the four sets of coordinates into this equation, solve any three of them for D,E,F, and then substitute these expressions into the fourth equation to give a homogeneous equation in the u_j quantities.  Thus we have

Expanding the determinants and collecting terms, this gives

where v_ij = x_iy_j – x_jy_i.  Notice that the quantities

represent half the signed areas of the triangles with vertices P_i, P_j, and P_k.  In terms of these areas the previous equation can be written in the form

Expanding the u_j expressions, we get a quadratic in the parameter ρ

The discriminant of this equation, given by the square of the middle parenthetical quantity minus the product of the first and third, is

which shows (as one would expect) that the discriminant is invariant under rotations and translations.  In fact, expressing the v and A functions in terms of the x and y coordinates and simplifying, we find that this expression factors as

Thus the two values of ρ that give parabolas through the four points are

This expression is invariant under transposition of any two indices, since the effect of any transposition is simply to negate the numerator and denominator.

Since the directions of the axes of symmetry of the two parabolas through any given four points in a plane) can be determined by solving a quadratic equation, it follows that lines with these directions can be constructed geometrically by Euclidean methods, i.e., using only straight-edge and compass.  Of course, not all four-point configurations correspond to parabolas whose algebraic expressions have real and finite coefficients.  Obviously if any one of the four points is inside the triangle formed by the other three, then the two implied parabolas and complex and identical, and the locus intersects with the real plane only in the original four given points (assumed real).  In this case the real and imaginary parts of the parabolic equation can be taken as the real coefficients of two real hyperbolas that intersect in the four points.  If any two of the lines connecting distinct pairs the four points are parallel, then the implied parabola has its vertex at infinity, and is represented graphically by those two parallel lines.

The condition for the configuration of points to give real parabolas can be inferred from the discriminant.  The solution is purely real if and only if the argument of the square root is positive.  The argument is A₂₄₃A₁₃₄A₁₄₂A₁₂₃, which is (one sixteenth of) the product of the signed areas of the four triangles that can be formed from three of the four given points.  The quantity is easily seen to be invariant under permutations of the indices, so we can number the four points arbitrarily.  The signs of the individual areas are positive (by convention) if and only if the indices proceed in the counter-clockwise direction.  All cases are one of the two types shown below.

For the convex arrangement on the left, the loops 243, and 142 proceed in the counter-clockwise direction, and the loops 134 and 123 proceed in the clockwise direction, so the product of the signed areas is positive.  On the other hand, for the non-convex arrangement on the right, the loops 243, 134, and 142 are counter-clockwise, and the loop 123 is clockwise, so the product of the signed areas is negative.

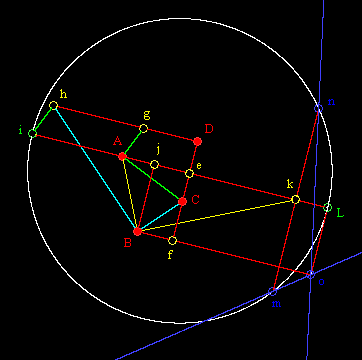
For the convex case, i.e., when none of the four points A,B,C,D is inside the triangle formed by the other three, we can construct (by Euclidean methods) lines parallel to the axes of symmetry of the two parabolas as follows:

-Let e and f denote the feet of the perpendiculars to CD from A and B respectively.

-Let g denote the intersection of the line through D perpendicular to CD, and the line through A perpendicular to AC.

-Let h denote the intersection of the line Dg and the line through B perpendicular to BC.

-Let i denote the intersection of the line Ae and the line through h parallel to Ag.

-Let j denote the intersection of the line Ae and the line through B parallel to Ae.

-Let k denote the intersection of the line Ae and the line through B parallel to AB.

-Locate the point L on Ae such that the segment kL has the same length and direction as the segment Aj.

-Draw the circle Q whose diameter is the segment iL.

-Let m and n denote the intersections of the line through k perpendicular to Ae with the circle Q.

-Let o denote the intersection of the line Bf with the line through L perpendicular to Ae.

-The lines mo and no are parallel to the axes of symmetry of the two parabolas through A, B, C, and D.

This construction for a typical configuration of points A,B,C D is illustrated in the figure below.

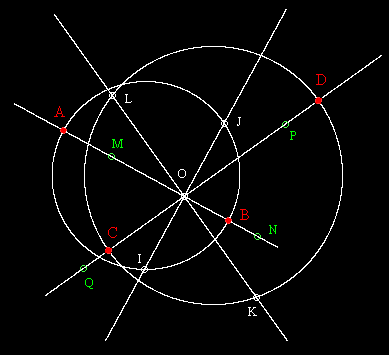
Pappus of Alexandria (c. 300 AD) gave a construction of the general conic through five given points in Book VIII of The Collection.  Isaac Newton treated the same problem in the Principia (1687), and then more explicitly in Arithmetica Universalis (1707).  In the latter he based the solution on finding the direction of the axis of symmetry, so it can be compared directly with the discussion above.  Newton's construction, given any four points A,B,C,D in the plane, is as follows:

- Let O denote the intersection of the lines AB and CD.

- Locate the point E on the line AB such that the segment OE is equal in length to OB and has the same sense as AO.  (If O is between A and B then E is at B.)

- Locate the point F on the line CD such that the segment OF is equal in length to OC and has the same sense as DO.  (If O is between C and D then F is at C.)

- Let G denote the circle on the diameter AE.

- Let H denote the circle on the diameter DF.

- Let I and J denote the intersections of the line through O perpendicular to AB and the circle G.

- Let K and L denote the intersections of the line through O perpendicular to CD and the circle H.

- Let M and N denote the points on AB that are a distance OI from O.

- Let P and Q denote the points on CD that are a distance OK from O.

- The quadrangle MPNQ is a parallelagram whose sides are parallel to the axes of the two parabolas that pass through the points A, B, C, and D.

This construction is illustrated in the figure below.

Incidentally, if we let f₁(x,y) = 0 and f₂(x,y) = 0 denote the equations of the two parabolas that pass through four given points, then obviously the quadratic curve given by

where μ is any constant. Thus we have a one-parameter family of conics, each of which passes through the four given points. In effect, the two parabolas are the basis elements for this family. Letting ρ₁ and ρ₂ denote the two values of ρ characterizing the two parabolas, we can write their equations as

The general member of the family has the equation

The discriminant of this quadratic equation is

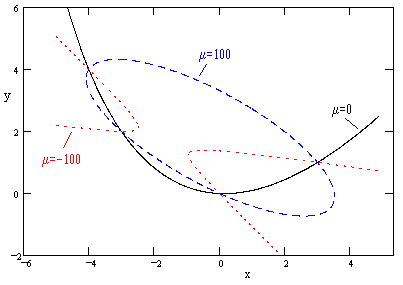
Thus we can find the conic through four points with any specified discriminant, since the discriminant is proportional to μ. To illustrate, consider again the example discussed above, based on the four points (0,0), (–4,4), (–3,2), (3,1). The figure below shows one of the basis parabolas along with the conics corresponding to μ = 100 and μ = –100. The other basis parabola is approached as μ goes to infinity.

Return to MathPages Main Menu