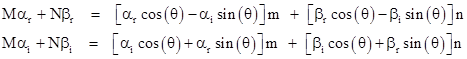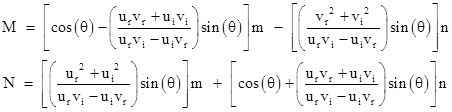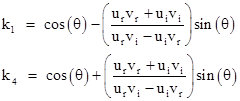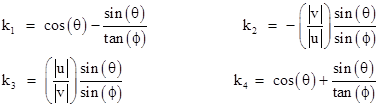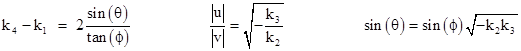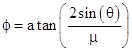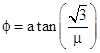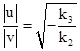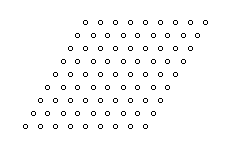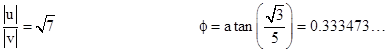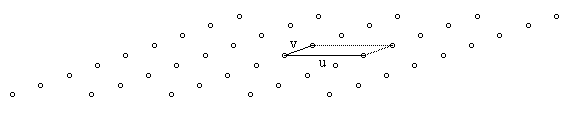The Crystallographic Restriction
The only possible rotational symmetries of a two-dimensional lattice are of order 2, 3, 4, or 6. To prove this, recall that a two-dimensional lattice, represented by points on the complex plane, is doubly-periodic in the sense that there are two complex numbers u,v such that mu + nv is a lattice point for every pair of integers m,n.
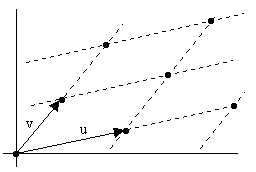
In order for this lattice to possess rotational symmetry of order k it is necessary for each lattice point to map to another under rotation through an angle q = 2p/k. In other words, for every pair of integers m,n, there must be another pair of integers M,N such that
Letting subscripts r and i denote the real and imaginary parts of u and v, we can expand this expression and separate the real and imaginary parts to give the two conditions
Solving these equations for M and N in terms of m and n, we get
This must give integer values of M and N for every pair of integers m,n, so it follows that the coefficients of m and n must all be integers. (For any fractional coefficients we can set m or n to 0 and the other to 1, yielding a fractional value of M or N.) Therefore, we have integers k1 and k4 such that
and so
This implies that the angle q must be such that cos(q) is either an integer or a half-integer. The only such values in the range -1 to +1 are -1, -1/2, 0, +1/2, and 1, corresponding to angles of 180, 120, 90, 60, and 0 degrees respectively. Thus the only (non-trivial) rotational symmetries are of order 2, 3, 4, or 6 (rectangular, triangular, square, or hexagonal).
Furthermore, if we let f denote the angle between the basis vectors (i.e., the phase difference between the complex numbers) u and v, then we have the expressions for the scalar and vector products
Therefore the expressions for M and N in terms of m and n can be written as
where
The determinant k1k4 - k2k3 is identically equal to 1. We also have the relations
Eliminating f from the first and third, we also have
From this we also get
To illustrate, we can set q equal to p/3 = 60 degrees, which is one of the four possible (non-trivial) values. In this case we have
and so k1 + k4 = 1. Now it appears we have some freedom of choice, because we can select integers k2, k3 such that -k2k3 - sin(q)2 is a square integer m2, and then compute the values of f, |u|/|v|, and k4 - k1, with which we can infer the individual (integer) values of k1 and k4. For any odd integer m we can put
and then we have
Thus k1 = (1-m)/2 and k4 = (1+m)/2. The individual coefficients k2 and k3 can be any factorization of (m2+3)/4, one positive and one negative. The angle f between the two basis vectors is given (in this example) by
The factorization of k2k3 is needed only to determine the ratio of the lengths of the basis vectors using the relation
The simplest possibility is to set k2k3 = -1 by putting k2 = -1 and k3 = 1. This corresponds to m = 1, which gives basis vectors of equal length, and the angle between them is f = 60 degrees. We also get k4 = 1 and k1 = 0, so the lattice transformation is M = -n, N = m + n. This gives the expected triangular lattice with 6-fold rotational symmetry shown below.
On the other hand, if we take m = 5 we get k2k3 = -7, and we can select the factorization k2 = -1, k3 = 7. In this case we get k1 = -2, k4 = 3, and
It may seem as if this gives a different lattice from the previous case, but if we plot the lattice points given by these expressions we get the figure shown below.
It is the same lattice as before, merely expressed in terms of different basis vectors. It follows that the "fundamental region" of a lattice is not unique, because the same lattice can be described in terms of different sets of basis vectors, corresponding to different fundamental regions. In order to arrive at a less arbitrary definition, we would stipulate that the basis vectors must be the smallest possible.