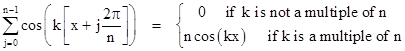Phased Summations

Given a function f(x) with period 2π, consider the function s_n(x) consisting of the sum of n copies of f(x) shifted in phase at uniform increments of 2π/n. In other words, we define the function s_n(x) as follows

If we expand f(x) into an exponential Fourier series

we can evaluate the previous summation on a term-by-term basis. This gives

Factoring e^ikx out of each term in the parentheses, this can be written as

Clearly if k is a multiple of n, the angular argument of each exponential in the parentheses is an integer multiple of 2π, so each of them equals 1, and the quantity in parentheses is simply n. On the other hand, if k is not a multiple of n, then let g denote the greatest common divisor of k and n, so that we have k = gκ and n = gν where κ and ν are coprime integers. In this case the expression in parentheses can be written as

The angular arguments have factors of 2π times the ratios 0/ν, 1/ν, 2/ν, ..., (gν–1)/ν, so we can reduce these modulo 2π to g copies of the sequence 0/ν, 1/ν, 2/ν, ..., (ν–1)/ν. Thus the above quantity can be written as

Since κ is coprime to ν, the set of integers 0κ, 1κ, 2κ, ..., (ν–1)κ comprises a complete set of residues modulo ν, so the expression in parentheses is just the sum of ν complex numbers uniformly located around the unit circle, so the sum vanishes identically. Therefore, all the components with k not a multiple of n in the expression for s_n(x) vanish, and we have the result

Essentially the same derivation can be performed for strictly real-valued functions. For a real-valued function f(x) the coefficients c_j and c_–j in the exponential Fourier series must be complex conjugates of each other, and if all the coefficients are strictly real the function can be expanded into a sum of cosines, i.e.,

Likewise if the coefficients are all strictly imaginary the function can be expanded into a sum of sines. A general real-valued function can be expressed as a sum of sines and cosines, but for simplicity we will consider just the cosine components. A similar analysis applies to the sine components.

The kth term of the cosine series is c_k cos(kx), and we can consider the sum of n copies of this general term with x replaced by x, x+2π/n, x+2(2π/n), x+3(2π/n), ..., x+(n-1)(2π/n). Using the trigonometric identity

each cosine in this summation can be written as

If k is a multiple of n, the arguments of the second factors in the two right-hand terms are integer multiples of 2π for any j, so in this case the first term is just cos(kx), the second term is identically zero, and the sum over the n values is n c_k cos(kx).

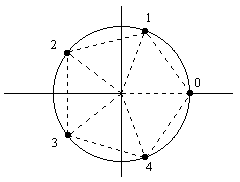
On the other hand, if k is not a multiple of n, then the quantities kj(2π/n) give evenly spaced divisors of 2π, so the sums all vanish. (The proof is the same as in the exponential derivation above.) This applies to both sine and cosine functions, as can be seen for the case n = 5 in the figure below.

The x coordinates of the five evenly spaced points on the circle are the cosines of the five values, and the y coordinates are the sines. By symmetry it's obvious that the average of those five points (or in general, the average of n points evenly spaced around a circle) is the center of the circle, which implies that the sum of the cosines and the sum of the sines are both zero for any n. Thus we have

Using this fact we can now easily evaluate the sum of n copies of an arbitrary periodic function f(x) with period 2π for evenly spaced arguments:

Thus, in essence, the Fourier series expansion of the summation of n shifted copies of an arbitrary periodic function consists of just (n times) the sum of the terms of the Fourier expansion of the original function whose indices are multiples of n.

If the only non-zero coefficients of the Fourier series expansion of the original function f(x) are for indices less than n, then obviously the resulting overall summation is just the constant nc₀. On the other hand, if the coefficient c_n is non-zero but all the higher order terms (with coefficient indices that are multiples of n) are zero, than the overall sum is n[c₀ + c_n cos(nx)], so it's a pure cosine wave with a constant bias. In general, the overall summation is an arbitrary function (not a pure sine wave) with frequency n times the frequency of the original function. Of course, this need not be the fundamental frequency, because it's possible for some of the leading coefficients in the original function expansion to be zero. For example, if the only non-zero coefficient of the original function is c_3n, then the fundamental frequency of the summation will be 3n times the frequency of the original function. But this occurs only because the spectrum of the original function has no lower-order components that are multiples of n. In general the frequency is the greatest common divisor of the frequencies of the non-zero components.

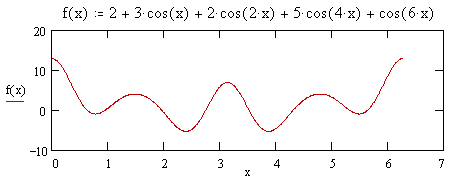
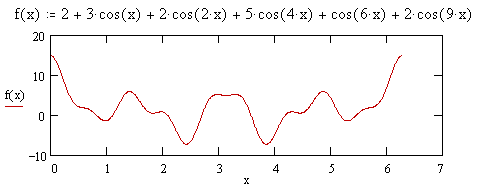
To illustrate, consider the function shown below.

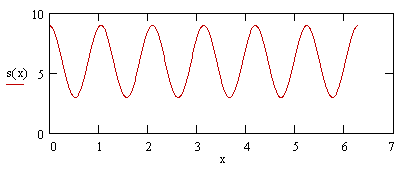
If we sum this function over 3 copies separated in phase by 2π/3, we get the result shown in the figure below.

This sum is simply s(x) = 3[2 + cos(6x)], because only the constant term and the 6th order term from the original function contribute. On the other hand, if we add a term 2cos(9x) to the function f(x) we have

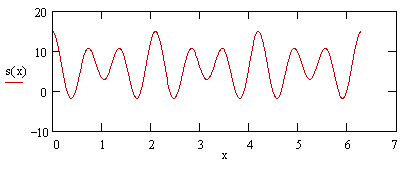
In this case there are two non-constant terms whose orders are multiples of 3. The sum of 3 copies of this function separated in phase by 2π/3 is therefore 3[2 + cos(6x) + 2cos(9x)], which is plotted in the figure below.

This has components with frequencies proportional to 6x and 9x, and the overall frequency is the greatest common divisor of these, which is 3x.

Return to MathPages Main Menu