|
Guessing Faster Than Light |
|
|
|
The second law of thermodynamics (at least in the context of classical kinetic theory) is often regarded as a very unusual fundamental law because it holds only with high probability, rather than with certainty. For example, it tells us that the molecules of a gas tend to disperse toward a uniform distribution, and yet there is some non-zero (albeit fantastically small) probability that the reverse process might take place, i.e., the molecules of a large cloud of gas could (in principle, given the reversibility of Newton’s laws of motion) converge into a smaller region, and the overall entropy might drop. Of course, this would require a very special initial cloud, but there nevertheless seems to be a sense in which the second law could be violated, given a sufficient amount of “luck”. |
|
|
|
It’s interesting to consider if there are any other fundamental laws that could be violated by chance. One of the basic tenets of modern physics is that information cannot be propagated faster than the speed of light. This is a subtle proposition in itself, because the meaning and ontological status of “information” is problematic. What is information? Is it ever created or destroyed? Does information have a definite spatial location, and can it be said to propagate? Without digressing into these questions, we may naively regard information as a particular string of one hundred 0’s and 1’s, selected at random (say, by tossing a coin repeatedly), and written on a piece of paper in some location. What is the soonest that this same string of one hundred binary digits could be written down on another piece of paper ten light years away? |
|
|
|
The usual answer is that the soonest the string of digits could be communicated to a distant location ten light years away is ten years, because no information can be communicated faster than light. However, it is theoretically possible (albeit fantastically improbable) that the same string of digits could be written down at the remote location simultaneously, just by guessing, or by a (presumably) independent series of coin tosses. In fact, there is a non-zero chance that this form of “communication” would work repeatedly. How would (or should) this be distinguished from “real” communication? |
|
|
|
Compare this with the fact that (according to quantum mechanics) a photon has a non-zero amplitude for traveling faster (or slower) than “the speed of light”. For any two events A and B there is a certain probability P(A,B) for a photon to be exchanged between those two events, and this probability is a function of the squared space-time interval
|
|
|
|
|
|
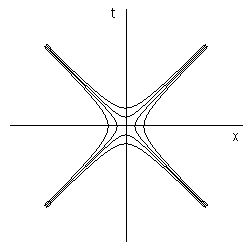
The probability is greatest for pairs of events separated by null intervals, i.e., with (dτ)2 = 0, but there is also a non-zero probability, proportional to the inverse of the squared interval, for an exchange of a photon between events separated by intervals greater than or less than zero. The phase angles for these “off-shell” exchanges are opposite, so they tend to cancel out when combined as intermediate jumps over long distances, but they are important over short distances and are always present to some extent, even over long distances. Of course, the only invariant measure of “distance” in Minkowski space-time is based on the magnitude of the interval defined above, which is zero for c-intervals, so in order to quantify the probability for light to be exchanged along non-c-intervals we need to consider the absolute magnitudes. Since the probability of a photon exchange between two events is a function of the absolute magnitude of the interval between those events, the envelope of probable exchanges can be illustrated as shown below. |
|
|
|
|
|
|
|
The maximum probability for the exchange of a photon with an object at the origin of these coordinates is for events along the diagonals through the origin, which are the null c-intervals, i.e., intervals with |(dt)2| = 0. However, there is a small non-zero probability of a photon exchange from the origin to an event on the inner hyperbolic locus shown in this figure, which is the locus of events separated from the origin by intervals with a fixed absolute magnitude. Likewise there is an even smaller (but still non-zero) probability of an exchange with an event on the outer locus, and so on. Clearly for large values of x the speed of the photon’s path approaches c for any fixed magnitude of the interval. |
|
|
|
Is there some relation between the improbable exchange of photons along non-null intervals, the improbable violations of the second law of thermodynamics, and the improbable pseudo-communication of binary strings by guessing? All of these seem to have implications for our conception of time. The proposition that entropy always increases with time has led some people to suggest that perhaps the increase of entropy is time. There are some obvious problems with this idea, but in any case there seems to be a close relationship between the directionality of time and the phenomenon of increasing entropy. From this point of view, the theoretical possibility that the second law could (with small but non-zero probability) be violated and entropy could spontaneously decrease then leads to questions about the direction of the “flow of time” in such circumstances. Likewise the potential for photons to be exchanged along non-null space-like intervals (i.e., faster than c) raises questions about the flow of time, since, if such exchanges could be counted on to occur consistently, we could send messages into the past. This would introduce many problems for the usual ideas of causality, but in fact causality is saved by the extreme improbability of photon exchanges along non-null intervals. Essentially we find that such exchanges are so improbable they cannot be used to convey information at a rate (or with a quality) that exceeds what could be achieved by random guessing. Thus it seems very closely related to our pseudo-communication method based on random guessing. |
|
|
|
These considerations suggest that there is not a sharp boundary between directional transference of information from one place to another and the spontaneous appearance of matching or correlated information at separate locations by random processes. |
|
|