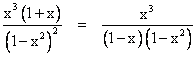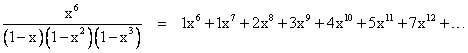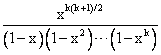Partitions Into Distinct Parts

For any positive integers n and k, let p_k(n) denote the number of ways in which the integer n can be expressed as a sum of exactly k distinct positive integers, without regard to order.  For example, the integer n = 12 can be expressed as a sum of three distinct positive integers in the following seven ways:

Therefore we have p₃(12) = 7.  Obviously p₁(n) = 1 for all n, so the generating function for p₁(n) is just the geometric series

The values of p₂(n) for n = 1, 2, 3, … are easily seen to be 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, … and so on.  In other words, p₂(1+2j) = p₂(2+2j) = j.  Factoring x³ and 1+x from the power series with these coefficients, we get

The infinite series on the right is just the derivative of the previous geometric series, except with x² in place of x, so we can differentiate the closed form of the geometric series and insert into this expression to give the generating function for p₂(n)

The first several values of p₃(n) are listed (by rows) below.

Just as every second term of the p₂(n) series gives an arithmetic sequence, we expect that the values of p₃(n) should give sequences of degree 2, and this is indeed the case, as can be seen by taking every sixth term.  The values in the columns are given by second-degree polynomials, i.e., we have

The generating functions for these individual sub-sequences are

The sum of these sub-sequences gives the generating function for the entire p₃(n) sequence.  The numerator of the sum is a (shifted) palindromic polynomial

Dividing this by the denominator and simplifying, we get the complete generating function for the number of partitions of n into 3 distinct parts

Notice that if x⁶ is replaced with 1 in the numerator the resulting expression would be the generating function for the number of partitions of n into positive integers (not necessarily distinct) no greater than 3.  We can see this immediately because each of the factors in the denominator contributes a geometric series in x^k where k is 1, 2, and 3 respectively, and hence the coefficient of xⁿ for n greater than 0 is the number of ways in which n is the sum of those three elements.  Therefore, letting P_j(n) denote the partitions of n into positive integers no greater than j (and defining P₃(0) = 1), we have shown that P₃(n) = p₃(n+6) for all n.  This correspondence can be represented pictorially as shown below for the case n = 5.

Each partition of 11 into distinct positive integers must have a smallest part of at least 1, a second smallest part of at least 2, and a third smallest part of at least 3, so we can begin with this triad of 6 dots, and then to each column we add zero or more dots, with the requirement that the number of added dots can never decrease as we go from the left-most to the right-most column.  The total number of additional dots to be added is 5, and with the stated restriction these rows can be interpreted as the partitions of 5 into positive integers no greater than 3.  By the same reasoning it follows that, for any positive integer k, we have P_k(n) = p_k(n + k(k+1)/2).  In other words, the number of partitions of n into positive integers no greater than k is equal to the number of partitions of n + k(k+1)/2 into k distinct positive integers.  Thus the generating function for the latter is

Return to MathPages Main Menu