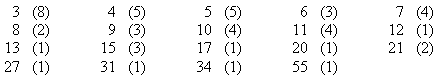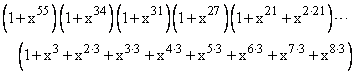|
Electoral Draws |
|
|
|
The principle of hereditary kingship became firmly established in most countries of western Europe during the middle ages, due partly to the historical accident that, for several centuries, each succeeding king by the time of his death had an adult son who seemed at least nominally capable of becoming the new king. Germany, however, was an exception. During these same centuries, a series of kings of Germany (who also held the title of Holy Roman Emperor) failed to leave any clear heir, either because they had no sons, or because their sons were still children when the king died. As a result, the question of succession had to be decided by other means. Gradually a system relying on a group of Electors was established. The Electors originally consisted of seven German dignitaries, who met after the passing of each king to select his successor. The number of Electors was later increased to nine. They were |
|
|
|
Archbishop of Cologne |
|
Archbishop of Mainz |
|
Archbishop of Trier |
|
King of Bohemia |
|
Count Palatine of the Rhine |
|
Duke of Saxony |
|
Margrave of Brandenburg |
|
(Duke of Bavaria) |
|
(Ruler of Hanover) |
|
|
|
The odd number of Electors was helpful in avoiding draws. It’s interesting that the titles of the Electors themselves (with the exception of the three archbishops) were strictly hereditary, so ultimately the system was still based on the principle of heredity, but allowing some degree of choice. |
|
|
|
The Electors chose the German kings for over 500 years, from the 13th century until they were finally abolished in 1806 during the Napoleonic era. Ironically, just 18 years before the final abolition of the German Electors, a new system of Electors was established for selecting the leader of the United States of America. When the constitution of the United States was written in 1788, the power to select a president was given to a group of Electors. However, unlike the German Electors, these Electors were not hereditary, but were to be themselves elected by the legislative bodies of each state of the union. Of course, the members of the legislative bodies were themselves elected, by popular vote of all the citizens. The framers might have considered making citizenship an elective office as well, but decided instead to let citizenship be hereditary. (It’s not so easy to completely eliminate the principle of heredity.) New citizens could also be created by naturalization. |
|
|
|
In practice the states soon began to allow the presidential Electors to be chosen directly by popular vote, bypassing the state legislatures. The original intent of the framers of the constitution was for the presidential Electors to exercise their own judgment in making their selections for President and Vice President, but the rise of the party system led to the practice of having each candidate Elector public ally declare his allegiance to one party, so by voting for a particular Elector the citizen is essentially voting for the presidential and vice presidential candidates of that party. Another innovation came about when the states realized that they could increase their relative influence by adopting a “winner-take-all” policy, whereby all the electoral candidates of the party that gets the most popular votes (in that state) are chosen. By winning the popular vote in a winner-take-all state with nine Electors, the presidential candidate receives all nine electoral votes, whereas if the Electors were chosen in proportion to the popular vote, the presidential candidate would usually get only five to his opponent’s four, giving only a one-vote difference. In the belief that candidates will pay more attention to a “winner-take-all” state than to a proportionate state, nearly all the states quickly adopted this policy. (One or two states still allow their Electors to be split between the parties, in proportion to the popular votes, but this is rare.) Of course, once all the states have adopted the winner-take-all policy, the relative advantage of this policy disappears, leaving only the disadvantage that it allows for the possibility of a presidential candidate winning the overall popular votes but losing the electoral vote. This has actually happened at least twice in United States history. |
|
|
|
In presidential elections the fifty states - plus the District of Columbia - have a combined total of 538 Electors. The number of Electors from a state equals the number of the states’ representatives in the House and the Senate, which depends (for the House) on the population of the state. Based on the population census of 2000, the number of Electors for each of the states are listed below (applicable to the presidential elections of 2004 and 2008): |
|
|
|
|
|
|
|
If we assume every state has a winner-take-all policy, a candidate can either win or fail to win each of the fifty-one regions, so the number of distinct possible outcomes (win patterns) is |
|
|
|
|
|
|
|
This represents over two-thousand trillion outcomes. |
|
|
|
One possible result of a two-candidate election is an electoral draw, with each candidate receiving exactly 269 electoral votes. This raises the question: In how many distinct ways can a candidate win exactly 269 votes? If we don’t distinguish between states with the same number of votes, then we are just dealing with the following multi-set of summands: |
|
|
|
|
|
|
|
A candidate can win 0, 1, …, or 8 of the three-vote states, and he can win 0, 1, …, or 5 of the four-vote states, and so on. Thus the total number of distinct win patterns for a candidate (not distinguishing between states with the same number of votes) is |
|
|
|
|
|
|
|
Of these, the number of win patterns giving exactly 269 votes is 40972162 (almost 41 million), which is about one out of 145. This is the coefficient of x269 in the expansion of the product |
|
|
|
|
|
|
|
Of all the possible vote totals, from 0 to 538, the one with the most ways of occurring is 269. |
|
|
|
If we distinguish between the states with the same number of electoral votes, then the number of distinct outcomes is increased, because each of the roughly 41 million win patterns can occur in multiple distinct ways. For example, a given win pattern may contain 5 of the 8 three-vote states, but there are C(8,5) = 56 ways of choosing five of those eight states. Applying the appropriate factors to each win pattern in the set of 269-winning patterns, we find that the number of distinct ways of winning exactly 269 electoral votes, is |
|
|
|
|
|
|
|
which is just over 17 trillion, about 1/132 of all 251 possible outcomes. |
|
|