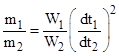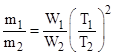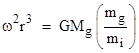Gravitational and Inertial Mass in Newton’s Principia

In the opening paragraph of the Principia, Newton defines the term "mass" to be used in his law of inertia, and says

It [mass] can also be known from a body's weight, for - by making very accurate experiments with pendulums - I have found it to be proportional to the weight...

Thus the proportionality between inertia and gravitational attraction is, for Newton's theory, an independent empirical fact, not something that follows from the first principles of the theory. Indeed, Newton himself observed (in Corollary 5, Proposition 6, Book 3) that this proportionality does not apply to forces in general, citing as an example the force of magnetism, which is not proportional to the mass of the attracted body. Thus the proportionality in the case of gravity is an accidental fact. In contrast, the identity between inertial and gravitational mass is a necessary and unavoidable feature of any theory (such as general relativity) that conceives of gravitational motion as nothing other than inertial motion in curved spacetime. In such a theory, inertial mass and gravitational mass are not just accidentally numerically equal, they are ontologically identical. As a result, general relativity is far more exposed to falsification than Newtonian theory, which is to say, general relativity is a much stronger theory.

Newton obviously recognized the importance of the absolute proportionality between inertia and weight, since he conducted many careful experiments to verify this fact. He discussed this proportionality in each of the three books of the Principia. In Book 3 he wrote

Others have long since observed that the falling of all heavy bodies toward the earth (at least on making adjustment for the inequality of the retardation that arises from the very slight resistance of the air) takes place in equal times, and it is possible to discern that equality of times, to a very high degree of accuracy, by using pendulums.

Book 2 contains Newton’s proof of the proposition that forms the basis of these pendulum experiments. Proposition 24 asserts that

In simple pendulums whose centers of oscillation are equally distant from the center of suspension, the quantities of matter are in a ratio compounded of the ratio of the weights and the squared ratio of the times of oscillation in a vacuum.

To prove this, he notes that the second law of motion implies that a force F applied to an inertial mass m for an interval of time dt results in a change in velocity equal to dv = (F/m)dt. Now, since the pendulum arms are of equal length, the ratio of forces applied to the pendulum bobs equals the ratio of the weights at any given angle from vertical. Therefore, the motive forces (at any given point of the arc) are in proportion to the weights. In other words, letting F(θ) denote the motive force at the point θ on the arc, we have F₁(θ)/F₂(θ) = W₁/W₂ for all θ. Thus the ratio of the equations of motion at any given θ can be written as

Noting that dv₁ = (dθ/dt₁)L and dv₂ = (dθ/dt₂)L where L is the length of the pendulum, we can substitute into this equation and re-arrange terms to give

(The use of dθ/dt_j rather than the more familiar dθ_j/dt in the expression of dv_j is nice example of Newton’s ingenuity.) This shows that the ratio of time increments for any given increment of θ is constant, so it equals the ratio of the total periods T₁/T₂. Making this substituting gives Newton’s Proposition 24, which is expressed symbolically as

Thus if we find (by experiment) that two simple pendulums of equal length swinging though equal arcs have equal periods, then it follows that the gravitational weights are proportional to the inertial masses. Returning again to Book 3, Newton wrote

I have tested this with gold, silver, lead, glass, sand, common salt, wood, water, and wheat. I got two wooden boxes, round and equal. I filled one of them with wood, and I suspended the same weight of gold (as exactly as I could) in the center of oscillation of the other. The boxes, hanging by equal eleven-foot cords, made pendulums exactly like each other with respect to their weight, shape, and air resistance. Then, when placed close to each other, they kept swinging back and forth together with equal oscillations for a very long time. Accordingly, the amount of matter in the gold (by book 2, prop. 24, corols. 1 and 6) was to the amount of matter in the wood as the action of the motive force upon all the gold to the action of the motive force upon all the [added] wood—that is, as the weight of one to the weight of the other. And it was so for the rest of the materials. In these experiments, in bodies of the same weight, a difference of matter that would be even less than a thousandth part of the whole could have been clearly noticed.

Newton’s ability to prepare equal weights of those nine diverse substances (gold, silver, lead, glass, sand, salt, wood, water, and wheat) may owe something to his alchemical experiments, but it’s surprising that he didn’t include mercury, which was one of the main ingredients in his alchemical recipies. Mostly likely he included wheat as an example of a highly pourous substance, but it may also have been selected as an example of an organic substance (along with wood).

These pendulum experiments are presented as the main empirical basis for Newton’s claim that weight is always proportional to mass, but he also considers the astronomical evidence for this proportionality. For example, he points out that if the moons of Jupiter were attracted to the Sun by a force that was disproportionate to their masses (in relation to the attraction of Jupiter itself to the Sun), their orbits would not be stable.

Surprisingly, Newton does not refer to what is perhaps the most direct and obvious astronomical evidence for the proportionality of inertial and gravitational mass, namely, Kepler’s third law. Recall that the centripetal force required to keep a body of inertial mass m_i moving with speed v in a circle of radius r is

where ω = v/r is the angular speed. This force is purely dependent on the inertia of the body, having nothing to do with gravity. Now, letting m_g denote the gravitational mass of this body, the gravitational force exerted on it by a large central body of gravitational mass M_g is

Equating this with the force required to keep the revolving body in its orbit, we get

This is, of course, nothing but Kepler’s third law, which expresses the observed fact that for every satellite of a given central body (such as the planets orbiting the Sun), the square of the angular speed times the cube of the orbital radius has the same value. It follows that the ratio m_g/m_i is the same for all the planets, despite the differences between their sizes, densities, and compositions. Likewise, since the moons of Jupiter also satisfy Kepler’s third law, it follows that the ratio of m_g/m_i is the same for all those moons, which range in size from Ganymede (roughly the size and mass of the smallest planet) to tiny boulders. We also know that small man-made satellites in orbit around the Earth have the same m_g/m_i as the Moon. Hence it’s clear that the proportionality of inertial to gravitational mass applies at least from the smallest objects up to objects the size of Jupiter. (Needless to say, this places very strict limits on any theory of gravity that implies shielding or saturation for sufficiently large or dense objects.)

Although the geometrical interpretation of general relativity seems to provide a compelling reason for the strict proportionality between weight and mass, this “explanation” has not been whole-heartedly accepted by all modern physicists. For example, in his “Lectures on Gravity” Richard Feynman emphasized the field approach to gravitation based on the spin-two graviton as the carrier of the force, and he wrote

It is one of the peculiar aspects of the theory of gravitation that it has both a field interpretation and a geometrical interpretation… the fact is that a spin-two field has this geometrical interpretation; this is not something readily explainable – it is just marvelous. The geometric interpretation is not really necessary or essential to physics. It might be that the whole coincidence might be understood as representing some kind of gauge invariance…

Steven Weinberg took a similar view in his “Gravitation and Cosmology”, where he regarded the equivalence principle itself as primary, and  treated the geometric interpretation as incidental. He wrote

…this geometrical analogy is an a posteriori consequence of the equations of motion derived from the equivalence principle, and plays no necessary role in our considerations.

Returning to Newton, it’s interesting that he immediately invoked the equality of inertial and gravitational mass to argue for the existence of vacuum. In Corollary 3 to Proposition 6 of Book 3 he says “all spaces are not equally full”, meaning there cannot be an equal quantity of inertial mass in each volume of space, because this would imply equal weight, and therefore a rock would not fall through the air. So some spaces must contain less matter than others. He continued “If the quantity of matter in a given space can, by any rarefaction, be diminished, why should it not be diminished indefinitely?” In Corollary 4 he contends that “If all the solid particles of bodies are of the same density, and cannot be rarefied, then a void, space, or vacuum must be granted”.

Return to MathPages Main Menu