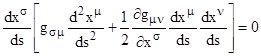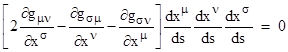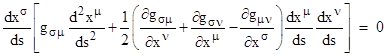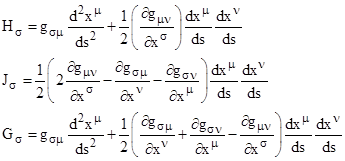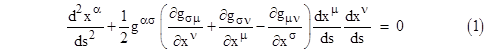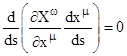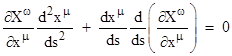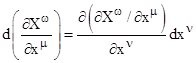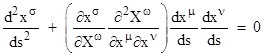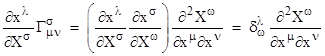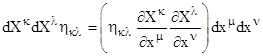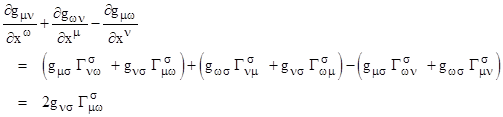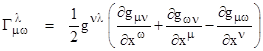Geodesics by Differentiation

The usual way of deriving the geodesic paths in an N-dimensional manifold from the metric line element is by the calculus of variations, but it’s interesting to note that the geodesic equations can actually be found simply by differentiating the metric with respect to the path length paramter. Beginning with the general Riemannian metric

where summation is implied over any repeated index in a single term, we can take the differentials of both sides as follows:

For the differential of each metric coefficient we can make the substitution

so we have

Furthermore, notice that the 2N² terms involving second differentials on the right hand side can be re-arranged into the form

Therefore, we have

Now, factoring dx^σ out of the right hand side, dividing through the entire equation by 2(ds)³, and noting that d²s/ds² = 0, we get

The expression inside the square brackets is similar to one form of the geodesic equations of the surface, but not exactly the same. However, notice that we have the identity

This can be directly verified by noting first that the expression in square brackets vanishes trivially if all the indices are equal, and then noticing that the combined coefficient of a given product of three derivatives vanishes if two indices are equal and one is different, and finally noticing that the combined coefficient of each product vanishes over the six permutations of all distinct indices. So, we can subtract half of this identically vanishing expression from the previous equation, giving the result

The expression inside the square brackets represents N quantities whose vanishing is the necessary and sufficient condition for a path to be stationary, i.e., for a path to be a geodesic of the manifold. (See the note Relatively Straight for a derivation of the geodesic equations by the calculus of variations.) Of course, the above expression does not imply the vanishing of the individual quantities inside the square brackets. It merely asserts that the sum of these N geodesic equations, each weighted by one of the derivatives dx^σ/ds, vanishes. However, this fact in itself has significant consequences. For example, since the weighted sum of the N geodesic equations vanishes identically, it follows that the N geodesic equations are not independent. If any N–1 of them are satisfied, along with the metric equation itself, then the Nth geodesic equation is also satisfied (except in the degenerate case when the associated derivative dx^σ/ds is zero).

Furthermore, since the displacement derivatives dx^σ/ds are the components of a contravariant vector, the preceding equation shows that the expression in square brackets is, in general, a covariant vector. Also, since the scaler product vanishes, it follows that this covariant vector is perpendicular to the displacement vector. Let us denote the contravariant vector with components dx^σ/ds by the symbol D^σ and then define the covariant vectors

Then we can summarize the previous results in the form

Thus all three of the vectors H, J, and G are perpendicular to the displacement vector D, which determines the direction of the path at any given point. Given this vector, we can then choose N–1 of the second derivatives d²x^σ/ds freely, leaving us with one equation in the one remaining second derivative. This is the same as saying that we can choose N–1 of the components of H (or of G) freely, and then the remaining component is determined. The path is stationary if and only if G_σ = 0, which means H_σ = J_σ. We know H and J are both perpendicular to D, but in general they can point in different directions and have different magnitudes. The vector H depends on the second derivatives along the path, whereas J depends only on the first derivatives, so by varying the second derivatives we can set H equal to J, resulting in a geodesic path.

By the way, we can isolate the second derivatives of the individual coordinates if we multiply through the geodesic equations by the contravariant metric g^ασ, which is the inverse of the covariant metric. This gives the convenient form

As an alternative approach to deriving the equations of geodesics on a Riemannian manifold, note that for any point we can define Riemann normal coordinates X^μ over a finite region around that point in terms of which the geodesics at that point satisfy the equations

These coordinates can, in principle, be established by measurements completely within the manifold. Our objective is to express this condition in terms of an arbitrary coordinate system x^μ related to the X^μ coordinates by a diffeomorphism. For any such coordinate system we have the relations

so we can divide by ds and substitute into the geodesic equation to give

Carrying out the differentiation, we get

The differential of the partial derivative in the second term is

Dividing through by ds and substituting into the previous expression gives

We can isolate the second derivative of each coordinate by multiplying through by the partial ∂x^σ/∂X^ω, noting that

Thus we have the geodesic equations

The expression in parentheses involves the partial derivatives of the arbitrary coordinate system with respect to the Riemann normal coordinates, in terms of which the geodesic equations are just the vanishing of the second derivatives of the coordinates. These expressions are called the Christoffel symbols of the second kind, denoted by

It’s useful to notice that we can multiply through by ∂X^α/∂x^σ to give the relation

and therefore

Now, if we can express the Christoffel symbol in terms of the metric coefficients and their derivatives, we will have an alternate means of arriving at the geodesic equations in the form given previously. To do this, we first form the product of two differentials of the Riemann normal coordinates to give

Multiplying through by the flat metric h_κλ , we have

This shows that the expression in parentheses represents the metric tensor coefficients with respect to the x coordinates, so we have

Taking the partial derivatives with respect to x^ω gives

Using (2) we can substitute for the second derivatives in this expression to give

Taking our clue from equation (1), we can use this to form the expression

Dividing both sides by 2 and multiplying by the contravariant metric g^νλ, we arrive at the expected result

This shows that we can derive the geodesic equations without explicitly using a variational technique, except to the extent that the original “straight line” assumption with respect to Riemann normal coordinates represents the result of a variational argument.

Return to MathPages Main Menu