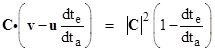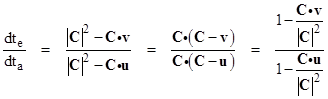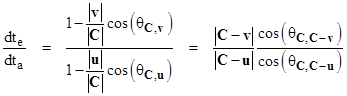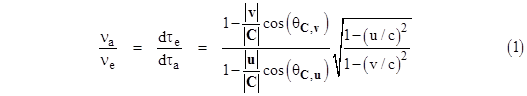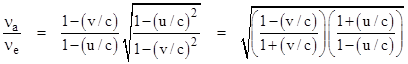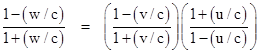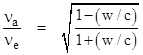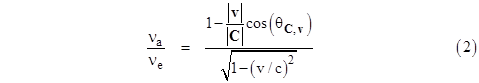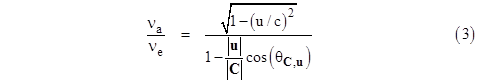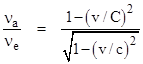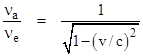The Doppler Effect

Consider a transmitter moving with constant velocity u, a receiver moving with constant velocity v, and a signal propagating with velocity C in terms of an inertial coordinate system in which the signal’s speed |C| is independent of direction. This would apply to a system of coordinates at rest with respect to the medium of the signal, and it would apply to any inertial coordinate system if the signal is light in a vacuum. It would also apply to the case of a signal emitted at a fixed speed relative to the transmitter, but only if we take u = 0, because in this case the speed of the signal is independent of direction only in terms of the rest frame of the emitter.

We immediately have the relation

where r_e and r_a are the position vectors of the emission and absorption events at the times  t_e and t_a respectively. Differentiating both sides with respect to t_a and dividing through by 2(t_a – t_e), and noting that (r_a – r_e)/(t_a – t_e) = C, we get

where u and v are the velocity vectors of the emitter and receiver respectively. Solving for the ratio dt_e/dt_a, we arrive at the relation

Making use of the dot product identity r∙s = |r||s|cos(θ_r,s) where θ_r,s is the angle between the r and s vectors, these can be re-written as

The frequency of any process is inversely proportional to the duration of the period, so the frequency at the absorber relative to the emitter, projected by means of the signal, is given by ν_a/ν_e = dt_e/dt_a.  Therefore, the above expressions represent the classical Doppler effect for arbitrarily moving emitter and receiver.

However, the elapsed proper time along a worldline moving with speed v in terms of any given inertial coordinate system differs from the elapsed coordinate time by the factor

where c is the speed of light in vacuum. Consequently, the actual ratio of proper times – and therefore proper frequencies – for the emitter and receiver is

The leading ratio is the classical Doppler effect, and the square root factor is the relativistic correction. To verify that this reduces to the usual relativistic Doppler effect for light rays between co-linearly moving transmitter and receivers, suppose the velocities u and v are in opposite directions, with v parallel to the light vector C, and with u anti-parallel. In this case the angle between C and v is zero, and the angle between C and u is π, so the cosines of these angles are +1 and –1 respectively. We also have |C| = c. Inserting these values into the above expression gives

It’s easy to show that if w is the relativistic composition of the co-linear speeds u and v, defined as w = (v–u)/(1 – vu/c²) then

so the relativistic Doppler effect for oppositely moving transmitter and receiver with light signals in the vacuum can be expressed purely in terms of the relative speed w between the transmitter and receiver as

Returning to equation (1), consider the case of a reference frame in terms of which the emitter is at rest, so u = 0 and equation (1) gives

Here the numerator is the classical effect (for both a wave theory with the emitter at rest in the medium and for an emission theory), and the denominator is the relativistic correction due to time dilation. On the other hand, in terms of the rest frame of the receiver we put v = 0 in equation (1), which gives

Now suppose that, relative to the receiver’s rest frame, the incoming pulses of the signal are arriving perpendicular to the receiver’s motion. This implies that C–v is perpendicular to v, so we have(C–v) ∙ v = 0. It follows that C∙v = |v|², and so cos(θ_C,v) = |v|/|C|. Inserting this into equation (2) gives

Thus if the signal propagates at the speed of light in vacuum, so C = c, the frequency shift in this condition is simply

whereas classically it would be the square of this. On the other hand, for the condition when the light signal is perpendicular to the receiver’s path in terms of the emitter’s rest frame, we have cos(θ_C,v) = 0, so in this case equation (2) gives

which is the reciprocal of the previous result. Thus the received signal in the “transverse” condition is either red-shifted or blue-shifted, depending on whether the transverseness is evaluated with respect to the receiver’s or the emitter’s rest frame.

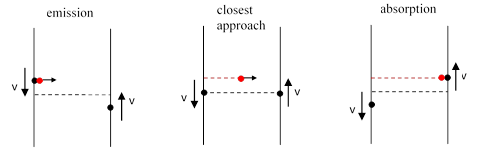
Naturally for a receiver moving in a straight line past a transmitter there is a point at which the proper reception frequency exactly equals the proper transmission frequency, i.e., the point at which the blue shift changes to a redshift. The preceding equations show that this does not occur when the path of the signal is perpendicular to the receiver’s path with respect to either the emitter’s or the receiver’s rest frame. It occurs for the pulse that is emitted perpendicular to the emitter’s path and received perpendicular to the receiver’s path, both evaluated in terms of the frame in which the emitter and absorber have the same speed.

A simple way of expressing this is to point out that the null frequency shift occurs for the pulse that travels the shortest distance from emitter to receiver, and this pulse is obviously neither emitted nor received at the point when the emitter and receiver are at their point of closest approach. Since the pulse requires an amount of time to traverse the distance between emitter and receiver, it must be emitted slightly before the point of closest approach and received slightly after. Of course, the spatial distance traveled by this pulse (for emitter and receiver on parallel paths) is equal to the minimum distance between the emitter and receiver, i.e., the perpendicular distance between the paths. This sequence of events for transmission of a null-shifted pulse is illustrated in the figures below.

Qualitatively this applies equally to both the classical and the relativistic treatments. (Since both emitter and receiver have the speed v relative to this system of reference, there is no differential time dilation.) Of course, due to aberration, the path of the “null shifted pulse” is not perpendicular to the path of either the emitter or receiver in terms of their own rest frame coordinates. It follows that the transmissions which are perpendicular relative to either of these rest frames have a non-null Doppler effect. The difference between the classical and relativistic treatments is in the magnitude of the effect.

The difference between the classical and relativistic treatments appears more clearly when we consider a receiver moving uniformly in a circle around a transmitter, or vice versa (in flat spacetime). This is a stationary configuration (up to spatial isotropy), so we can definitely say the spatial distance traveled by the signal pulses is not changing. Classically it would follow that there was no Doppler effect, but the time dilation of special relativity implies that the proper time of the circling entity is reduced relative to the rest frame time coordinate of the central entity. As a result, the received signal will be either red-shifted or blue-shifted, depending on whether the transmitter or the receiver is moving in a circle.

Return to MathPages Main Menu