Hawking Radiation and Super-Acoustic Diffusion

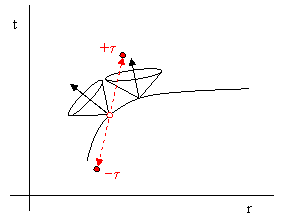
In some popular accounts Hawking radiation is attributed to quantum tunneling. According to this explanation, vacuum fluctuations inside the event horizon lead to pairs of virtual particles and anti-particles, and one of these may “tunnel” across the event horizon to the exterior of the black hole. The particles are called virtual because the intervals over which they act are spacelike, meaning that they are outside the lightcone. Ordinarily, in flat spacetime, two such virtual particles would re-combine, giving no net effect. However, in the presence of a spherically symmetrical gravitational field there exists non-zero curvature of spacetime, manifested as tidal effects and acceleration of the free-falling frame relative to the “stationary frame” of the Schwarzschild time coordinate. In this context, the spacetime intervals of the particles produced by a vacuum fluctuation are as shown below.

The vacuum fluctuation is centered at the vertex of the inner lightcone, and produces two virtual particles, as indicated by the spacelike character of the intervals shown in red relative to the inner lightcone. However, due to the tidal effects of gravitational curvature, those intervals are actually timelike with respect to the outer lightcone, with one particle proceeding in the positive time direction and the other proceeding in the negative time direction. Thus, even though the two particles are virtual from the standpoint of the free-falling system of reference at the point of origin, they are real (one with positive and one with negative mass-energy) from the standpoint of a nearby system of coordinates. The particle with positive energy radiates away (although it might fall back if it is a massive particle with insufficient velocity to escape), and the other particle has the effect of conveying negative energy to the black hole from the standpoint of the external spacetime. It might also be said that the work done by the tidal forces to separate the two particles represents an outflow of energy, diminishing the energy content of the black hole by an amount equal to the mass-energy of the radiated particle. (The potential for particles to be either virtual or real depending on the state of acceleration of the reference system also exists in flat spacetime for accelerated observers, and is known as Unruh radiation.)

The popular description of Hawking radiation in terms of localized discrete particles can be slightly misleading, because the actual calculations are based on a more global analysis of the frequency composition of propagating vacuum fluctuations in the distant past (prior to the formation of the black hole) and the distant future. This analysis shows that the future field behaves as if the black hole radiates at a rate proportional to the strength of gravity (i.e., the curvature) at the event horizon. The larger a black hole, the more mild is the curvature at the horizon, so the lower is the rate of radiation. This is why the radiation would be appreciable only for extremely small black holes.

The possibility of energy tunneling across an event horizon exists (according to quantum electrodynamics) because a photon has a certain non-zero amplitude for propagating along space-like intervals. The amplitude for superluminal propagation is significant mainly for distances smaller than one wavelength. Hawking radiation relies not only on the existence of vacuum fluctuations but on the superluminal propagation of quantum action. In this regard it’s interesting to recall that when Maxwell deduced the characteristic propagation speed of electromagnetic field disturbances is his 1873 Treatise he also included a discussion of a diffusion process by which some (albeit exceedingly small) amount of energy would be propagated at super-luminal speed. (See the note on Propagation of Pressure and Waves for a review of Maxwell’s analysis.) Is there any conceptual connection between Maxwell’s superluminal diffusion of electromagnetic energy and Hawking’s black hole radiation?

One way of trying to answer such questions is to re-express them in a more familiar context. Recently there have been studies of phenomena analogous to Hawking radiation in the context of ordinary acoustics within an inviscid irrotational fluid. The analog of an event horizon is defined as a closed surface over which the inward velocity of the fluid exceeds the speed of sound (i.e., the speed of propagation of acoustic disturbances). Setting aside the practical feasibility of such an arrangement, it is at least understandable how the enclosed region could be regarded as an acoustic black hole, since (one would think) no acoustic disturbance inside the region could propagate to the exterior of the region. In essence we can consider just a uniform volume of fluid moving to the left (relative to a given frame of reference) at a speed exceeding the speed of sound, and note that no acoustic disturbance introduced to that fluid can propagate to the right, because that would require super-acoustic propagation. Equivalently, we can imagine a stationary volume of fluid with an event horizon conceived as a plane surface moving to the right at the speed of sound. Ordinarily we would say that no acoustic disturbance behind this surface can propagate to the other side of the surface, so it can be regarded as a moving event horizon.

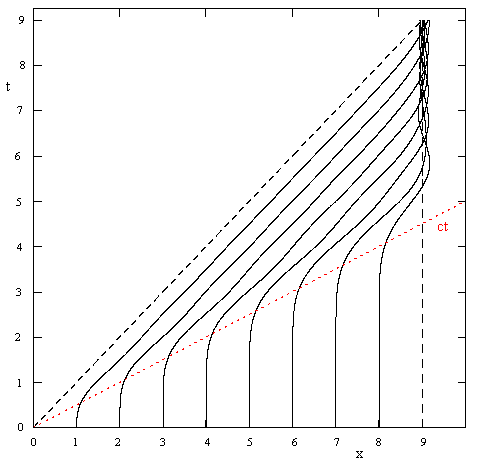
Now, in this form, the situation is precisely the same as what is analyzed in the note on propagation of pressure and waves. In that note we modeled the microscopic mechanism of a general acoustic medium (in one space dimension) as a series of small discrete masses and springs, representing the molecules and inter-molecular forces comprising a macroscopic volume of gas. We showed how the effects of a disturbance at any point propagate through the medium, and how the acoustic speed emerges as the leading edge for almost all of the propagated effects. This is illustrated in the plot below for a typical case.

Initially there are ten stationary masses at the locations x = 0, 1, ..,9, and at time t = 0 the mass at location x = 0 is abruptly set in motion at half the speed of sound. (The mass at x = 9 is held stationary throughout.) The line marked as “ct” represents the event horizon, and the plot shows how the position of each mass is nearly unaffected until the event horizon has passed through. In other words, the disturbance is confined (almost) entirely to the region behind the event horizon.

Nevertheless, there is a small effect that propagates super-acoustically, as can be seen from the fact that each mass begins to move slightly ahead of the arrival of the event horizon. If we examine the mass positions more closely, we find that they each show some movement for every time greater than zero. Maxwell compared this to the diffusion of heat in a conductive solid, in accord with Fourier’s equation, and noted that

If we attempt to measure this velocity by ascertaining the time requisite for the production of a given amount of disturbance at a given distance from the origin of disturbance, we find that the smaller the selected value of the disturbance the greater the velocity will appear to be…

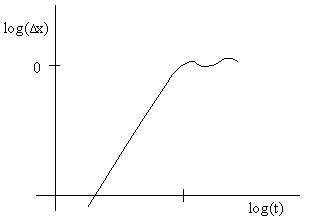
Thus, according to Maxwell, there is no upper limit on the speed of diffusion. Of course, the amount of disturbance becomes exponentially small at times ahead of the acoustic limit, but in principle (according to Maxwell) some non-zero effect is present at all velocities. This diffusion effect is visible in the results of our simple mass-spring model, in which the displacement of each mass as a function of time has the characteristic shape shown below.

0

We could interpret this is signifying that Maxwell was describing a kind of Hawking radiation, in the sense that a small amount of energy could diffuse out from an event horizon. This diffusion is inherently non-local, because (unlike a propagating wave) the diffusion has infinite propagation speed and therefore does not represent a localizable entity. On the other hand, we described in the previous note why Maxwell’s view of electromagnetic diffusion was incorrect, because he assumed a medium with permittivity equal to zero, which would imply an infinite speed of wave propagation, contrary to the observed facts. In addition, we explained that the super-acoustic propagation in our mass-spring model was really an artifact of the action-at-a-distance property of the idealized springs. As the number of discrete mass-spring elements is increased, and the size of the springs is reduced, the super-acoustic effect is reduced, and the effect would disappear entirely in the continuous limit, corresponding to a continuous fluid.

Of course, a real gas is not actually continuous. It consists of discrete molecules and inter-molecular forces, somewhat similar to our mass-spring representation, and the inter-molecular forces in a real gas, while not instantaneous, do indeed propagate super-acoustically. To be precise, the electromagnetic forces between gas molecules propagate at the speed of light, which is nearly instantaneous compared with the acoustic speed in a real gas. Hence we should not be surprised by the presence of some super-acoustic effects in a gas. One well-known example is infrared radiation, which conveys radiant heat from one part of a gas to another at super-acoustic speed. Of course, this mode of energy transfer can still be regarded as waves, the only difference being that the waves are electromagnetic rather than acoustic, so the speed of propagation is the speed of light rather than the speed of sound. In contrast, the super-acoustic diffusion of pressure illustrated in the mass-spring model of a gas represents a mode of energy propagation that is distinct both from purely acoustic waves and from purely electromagnetic waves. The propagation speed of diffusion of variations in pressure (in the limit of small disturbances) approaches the speed at which variations in the inter-molecular forces are propagated. Thus by representing the inter-molecular forces with idealized springs, which exert forces at both ends as an instantaneous function of the displacement, we arrived at essentially instantaneous diffusion in the sense described by Maxwell. In a more realistic model, if we replace the springs with electromagnetic forces in which changes propagate at the speed of light, the limiting speed of diffusion would be the speed of light. It might be possible to regard this kind of super-acoustic propagation as analogous to Hawking radiation, in the sense that it provides a mechanism for pressure variations behind an acoustic event horizon to “out-run” the horizon and propagate energy (albeit of extremely slight magnitude) out to arbitrary distances ahead of the horizon.

But this mechanism relies on the underlying electromagnetic action, which propagates super-acoustically. If we consider an actual event horizon, characterized not by some acoustic speed, but by the speed of light itself, the applicability of this analogy to Hawking radiation becomes questionable. The dynamics of an acoustic medium are established by electromagnetic forces whose speed of propagation is nearly infinite in comparison with the acoustic speed of the medium, so it can facilitate super-acoustic diffusion, but for an actual relativistic event horizon, characterized by the speed of light, it would seem that we cannot appeal to any underlying structure to provide diffusion upstream through the horizon – at least not classically. But according to quantum electrodynamics a photon has a non-zero amplitude for being exchanged over arbitrary intervals, even over spacelike intervals, although the amplitude for super-luminal intervals becomes negligible for long range interactions. Our simple mass-spring model showed how the aggregate of short-range instantaneous interactions yields non-zero diffusion over long distances for all finite speeds of propagation, so it might be interesting to explore whether a consistent model of Hawking radiation could be developed on this basis.

From a naïve standpoint, there are a couple of puzzling aspects to Hawking radiation. One concerns how the vacuum fluctuations are distributed in a locally Lorentz-covariant way. The predicted magnitude of the radiation must depend on what fraction of the vacuum fluctuations act along intervals that, although spacelike relative to the local free-falling coordinates, are timelike with respect to the stationary external coordinates. The local frames of reference are uniformly parameterized by the real numbers from negative to positive infinity, but mathematically there does not exist a uniform distribution over the real numbers, so it isn’t clear how the vacuum fluctuations can be distributed in a Lorentz covariant way. (Of course, this question applies to quantum field theory in general, not just to Hawking radiation.) Another puzzling aspect concerns the representation of forces by means of the exchange of virtual particles. The question is whether this means of expression represents the actual causal structure. In classical electromagnetism the choice of a “gauge” leads to what might be mistaken for different causal relationships. For example, in the Coulomb gauge the electric potential is an instantaneous function of the positions of the charges, whereas in the Lorenz gauge the potentials are retarded by the lightlike propagation time. In a sense, the Coulomb gauge is analogous to the mediation of forces by virtual particles, and yet it can be shown that the causal structure of electrodynamics actually follows the Lorenz gauge, meaning that no information or energy can be communicated faster than the speed of light. This continues to be true in quantum field theory, so any effect that relies on or implies superluminal conveyance seems questionable. This is the same argument that undermines Maxwell’s superluminal diffusion.

Return to MathPages Main Menu