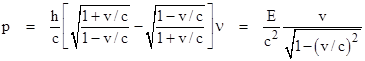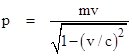Another Derivation of Mass-Energy Equivalence

The equivalence of mass and energy expressed by the relation E = mc² is a fairly direct consequence of Maxwell’s conception of electromagnetic waves. According to Maxwell’s equations, the energy density of electric and magnetic fields e and b is (e² + b²)/(8π) and the momentum density is (e x b)/(4πc). Thus in the case of radiation (when e and b are equal and orthogonal) the energy density is E = e²/(4π) and the momentum density is p = e²/(4πc), so we have the important relation p = E/c. In addition, the energy of a pulse of light for relatively moving systems of reference transforms in proportion to its frequency, consistent with Planck’s relation E = hν. Given these facts, we can show that light pulses of total energy E reflecting inside a closed container contribute E/c² to the inertial mass (i.e., the resistance to acceleration) of the container.

Consider two stationary mirrors, facing each other, with two monochromatic light pulses of equal intensity bouncing back and forth, with combined energy E = 2hν, such that each mirror is struck simultaneously. Immediately after one of these simultaneous bounces, we impart to the mirrors a small speed v. One of the photons will now be red-shifted and the other blue-shifted relative to the mirrors, and this transition results in a net impulse to the mirrors, resisting their acceleration. To the first order of approximation, using the Doppler shift formula, the difference between the momenta of the two pulses is

To the same order of approximation, Newton’s law of inertia gives p = mv, and therefore m = p/v, so the above relation implies E = mc².

The above derivation is similar to an idea of F. Hasenohrl in 1904. In that year Hasenohrl published a paper in Annalen der Physik (the same journal where Einstein’s papers on relativity would appear in the following year), in which he considered a closed container with perfectly reflecting interior walls, and found that the inertia of the container was increased by an amount proportional to the energy of the radiation it contained. Oddly, he initially concluded that E = (3/8)mc², and then in 1905 he published a follow-up paper (in the same journal), revising this to E = (3/4)mc². In a sense it is more ambitious to try to determine the effect of the radiation on the entire container, because the pressure of the radiation implies that the walls of the container are stressed (like a spring), and this represents additional energy that must be taken into account. The same complication arose when evaluating the mass of an electron (for example) in classical electrodynamics, because in addition to the energy of the electro-static field we must also consider the forces necessary to hold the electron together. For simplicity, in the derivation above we have considered only the inertia represented by the radiation itself.

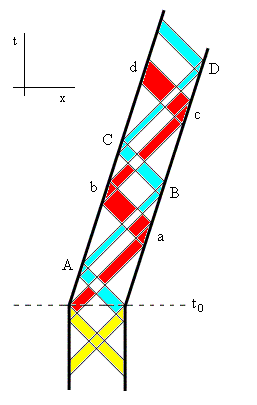
It’s interesting to examine the sequence of events of our derivation in detail. The space-time diagram below gives a pictorial representation.

The pulses have been shown with positive widths, to indicate the elapsed proper times, inversely proportional to the frequencies. The velocity v is imparted to the mirrors at time t₀. Prior to that time the two light pulses strike the mirrors simultaneously (in terms of the initial rest frame) with equal and opposite momenta, so they don’t exert any net impulse to the mirrors. After time t₀ one of the pulses is blue-shifted (in terms of the new rest frame), striking the mirrors at events A, B, C, D, …, and the other pulse is red-shifted, striking the mirrors at events a, b, c, d, and so on. In terms of the new rest frame of the mirrors, the impacts A,a are not simultaneous, nor are the impact b,B, although the latter are simultaneous in terms of the original rest frame. It’s worth noting that even though the light pulses both have the speed c in terms of the new rest frame, they are not symmetrical, because one retains its blue shift and the other retains its red shift. Of course, this assumes perfect reflections, whereas a real barrier would absorb and scatter some of the light, so the interior region would tend toward thermal equilibrium. Nevertheless, for the first several cycles, the distinct red and blue-shifted pulses would persist, giving evidence of the former state of the system, and of the acceleration.

Incidentally, the approximations used in the preceding discussion don’t really reduce the validity of the derivation, because the expressions are exact in the limit as v goes to zero, and we can then integrate the effect to give accelerations of any magnitude. However, if we wish, we can carry out the same derivation in exact terms, without using any approximations. The difference between the momenta of the two pulses is given exactly by the formula

Now, the actual relativistic expression for the momentum of a rest mass m moving at speed v is

Substituting into the previous equation gives (exactly) the relation E = mc².

In a sense, the inertia of electromagnetic energy is already implied by the proposition that electromagnetic waves have momentum. Historically there were differing ideas about whether light exerts pressure. For example, Kepler suggested that pressure of light from the Sun might be responsible for the tails of comets. There were attempts as early as 1708 (Homberg) to detect such pressure, but it turned out to be very difficult to distinguish between the effects of differential heating versus the effects of actual radiation pressure. Interestingly, for a long time it was thought that only a corpuscular theory of light could account for light pressure. Apparently it was thought that a wave in a medium, especially a transverse wave as light was known to be, would not produce any longitudinal pressure. Nevertheless, Maxwell’s theory of transverse electromagnetic waves implies that a pressure is induced by a plane wave impinging on a surface. However, according to Maxwell’s conception, the pressure was a manifestation of stresses in the ether interacting with matter. Pressure can be a static phenomenon, like pressing on a wall with a cane. No momentum is conveyed by this pressure. Likewise Maxwell apparently didn’t think of the pressure of electromagnetic waves in terms of momentum. The concept of momentum seems to suggest a substantial entity moving from place to place, rather than a transverse wave propagating from place to place through a medium with essentially no longitudinal displacement. It’s interesting that Maxwell often spoke about the need for a medium to serve as the receptacle for light energy during the time between emission at one place and absorption at another, but he never spoke about the corresponding need for a corpuscular theory of light to account for the conveyance of momentum.

In 1876 Adolfo Bartoli put forward an interesting argument in favor of light having pressure. He pointed out that, by means of the Doppler effect, the radiant temperature of a cold body can be raised by reflecting its light from a moving mirror, and in this way it is possible to arrange for energy to flow from a colder to a hotter body. This would violate the second law of thermodynamics if the light did not impart a pressure to the mirror. This is the kind of principle-based reasoning that was later used to effectively by Einstein. In fact, it was Einstein who later explained the photo-electric effect by re-introducing some aspects of a corpuscular theory of light, including the conveyance of directed momentum.

In action-at-a-distance theories the transfer of momentum is conceived to take place directly between material bodies, so the interpretation of pure energy and disembodied momentum is more obscure. For example, in our preceding illustration of light pulses bouncing between two mirrors, the distant-action theories would regard the interactions as taking place directly between the mirrors, with no intervening entities. It isn’t clear how the concept of mass-energy equivalence would emerge in such a context.

Return to MathPages Main Menu