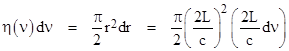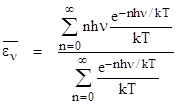The Necessity of the Quantum

If a flexible solid bar, held stationary at its ends, is struck at the midpoint, the energy of the blow will initially be absorbed by the lowest energy mode of the bar. This mode consists of a single coherent oscillation of the entire bar, with every part of the bar “in phase” with all the other parts. However, as time passes, some of the energy will flow into energy modes with progressively higher frequencies, shorter wavelengths, and smaller amplitudes. Eventually the low-frequency modes will dampen out completely, and the bar will return to a macroscopic state of apparent rest, but the energy of the blow has not disappeared, it is still present in the increased agitations of the elementary molecules comprising the bar. These agitations, which are highly incoherent fluctuations of very high frequency and small amplitude, represent heat energy, so the temperature of the bar is greater than in the original state of macroscopic rest, as depicted below.

This process is an example of the general principle that energy tends to spread out into all the available modes of a physical system. In fact, one of the fundamental propositions of statistical thermodynamics and the kinetic theory of gases is that, at thermodynamic equilibrium, the energy of a system is distributed equally into all the available energy modes, which correspond to the degrees of freedom of the system. For example, the molecules of a monatomic gas have only a single degree of freedom, namely, the positions of the molecules, so the only energy mode is the translational kinetic energy. In contrast, a diatomic molecule has two additional degrees of freedom, namely, the separation between the two parts of the molecule and the orientation of the molecule, so it has three energy modes, including the vibratory and rotational kinetic energy. At equilibrium, the energy of a quantity of gas is equally distributed between these three modes, whereas the thermodynamic temperature depends only on the translational mode, so more energy is required to raise the temperature of a diatomic gas by a given amount. (Thus the specific heats capacities of diatomic gases are greater than those of monatomic gases.)

Consider what would be expected to occur if the flexible bar was regarded as a continuous substance rather than as composed of discrete irreducible molecules with a limited range of frequency response. In that case there would be an infinite sequence of energy modes, of progressively higher frequencies and shorter wavelengths. Hence the energy of an initial disturbance would continue to be spread out over more and more energy modes, never actually reaching equilibrium. The energy would continue to evolve to less and less perceptible form, and would soon fall below any given threshold of detectability. If such was the case, it’s arguable whether the principle of energy conservation would have much significance. In order for the world to be anything like what we experience, there must be some cutoff point on the frequencies over which a given amount of energy can be distributed. This cutoff point appears in the thermal range, so all coherent forms of energy tend to devolve toward the incoherent form of energy called heat. (The number of effective degrees of freedom is greater in the regime of ultra-high frequencies and small amplitudes, so a uniform partition of energy over all the degrees of freedom results in nearly all the energy eventually being in the form of “heat”.)

Similar considerations apply to electromagnetic radiation confined within an enclosure. The magnitude of the electric field is constrained to be zero at the walls, so we expect the energy to be distributed among standing waves whose wavelengths are sub-multiples of the length of the enclosure. Again, from the classical perspective, the equipartition of energy applies, and hence the total energy at equilibrium should tend to spread out uniformly over all frequencies… but this again leads to the untenable conclusion that the energy would inexorably leak away into modes with higher and higher frequencies and smaller amplitudes. This obviously erroneous implication of classical physical principles was called “the ultra-violet catastrophe”, a name suggestive of the notion that all energy would inexorably flow into the high-frequency end of the spectrum, and that this conclusion is devastating for classical physics.

As discussed above, the potential for an ultra-violet catastrophe is actually present in the ordinary mechanics of vibrating strings, etc., so one might wonder why it wasn’t recognized much earlier in history. However, the recognition relies crucially on the equipartition of energy and related thermodynamic concepts, and these were not developed until the 19th century as part of the kinetic theory of gases, which was explicitly based on the atomistic doctrine. Thus the necessity of elemental irreducible entities wasn’t recognized until a theory based on just such entities was actually developed. It’s fair to say that quantum theory began with the atomistic doctrine of Democritus, and the first physical variable to be quantized was mass. From the study of the implications of quantized atoms of matter came the concept of the equipartition of energy, but the “catastrophic” implications of this weren’t immediately apparent, because the kinetic theory was already quantized and possessed the requisite cutoff point. The conundrum became apparent only when the equipartition principle was subsequently applied to the analysis of physical processes that had not (yet) been quantized, namely, electromagnetic waves, so no concept of a cutoff frequency existed.

One of the premises underlying the study of cavity (black body) radiation in the late 19th century was that the cavity could support a standing wave with wavelengths that were sub-multiples of the dimensions of the container. Consider an elastic particle whose velocity vector has components v_x, v_y, v_z bouncing freely inside a cubical container of size L x L x L will have a period of 2L/v_x in the x direction, 2L/v_y in the y direction, and 2L/v_z in the z direction. If we imagine a plane wave with the same normal velocity vector as this particle, then the wave will have the same periods in the three directions, and we can determine the corresponding wavelengths, which must be of the form λ_x = 2L/n_x , λ_y = 2L/n_y , λ_z = 2L/n_z , where L is the distance between the walls and n_x, n_y, n_z are any positive integers. The frequency components are therefore ν_x = cn_x/(2L), ν_y = cn_y/(2L), and ν_z = cn_z/(2L), where c denotes the phase speed of the wave (i.e., the speed of light) and the overall frequency of this standing wave is

The number of distinct waves with frequencies in a small range between ν and ν+dν is equal to the number of distinct triples of positive integers n_x, n_y, n_z such that the corresponding frequency given by the above equation falls within the range. These triples are distributed uniformly (with density 1) in the “+++” octant of a 3-dimensional lattice space, and the radial distance parameter in this space is r = 2Lν/c. Thus we have dr = (2L/c)dν. Letting η(ν)dν denote the number of waves in the incremental range, and recalling that the surface area of one octant of a sphere is πr²/2, we have

At this point, in order to represent the true number of distinct waves, we need to multiply the above by 2, because electromagnetic waves have two possible states of polarization. Applying this factor, and noting that the volume of the cube is V = L2, we arrive at

The function η(ν) represents the spectral density of allowable standing waves in a cavity of volume V, and it can be shown that this applies to arbitrarily shaped enclosures, not just to cubes. Now, from the classical point of view, the principle of the equipartition of energy leads us to believe that the energy in the cavity should be uniformly distributed over each of the energy modes, i.e., each of the allowable standing waves, so the power spectrum radiated from a cavity (at equilibrium) ought to have a distribution proportional to (1). Specifically, each wave should have an average energy of kT where k is Boltzmann’s constant and T is the temperature. (The energy of each “mode” is actually predicted to be kT/2, but each oscillating wave has two energy modes, between which the energy flows back and forth, so the total is kT.) Hence the energy density per unit volume as a function of the frequency should be (assuming the classical equipartition law is correct)

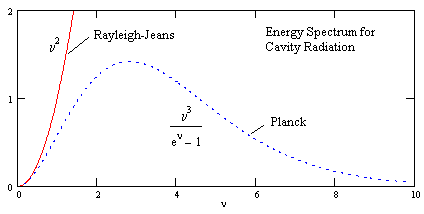
This is called the Rayleigh-Jeans law of blackbody radiation. Although this formula agrees with the actual blackbody spectrum at very low frequencies, it goes to infinity as the frequency increases, whereas the actual measured spectrum obviously does not. Also, the Rayleigh-Jeans law implies that essentially all the energy must flow to higher and higher frequencies - just as in the case of mechanical vibrations in the hypothetical continuous bar discussed previously. If this were the case, the energy would never reach equilibrium, but would be dissipated more and more over the infinite range of frequencies. Clearly one or more of the premises underlying this analysis are not correct.

In his work on the “ultra-violet catastrophe”, Planck reconsidered the equipartition of energy, according to which the mean energy in a particular mode (at equilibrium) is independent of the frequency of that mode. This conclusion from classical statistical mechanics follows from the Boltzmann distribution for the energy ε of a given mode, which is really just the exponential distribution

This is a proper density distribution (the integral from zero to infinity equals 1), and the mean value of ε with this distribution over the range from zero to infinity is kT, regardless of the frequency of the mode, so this implies the equipartition of energy (which we know leads to non-sensical results). This distribution can be derived classically in several different ways, but in general it corresponds to the proposition that states with higher energy are less probable (or less populated), and the weight factors of any two states are inversely proportional to the exponentials of their energy levels. In turn this is related to the idea that the weight factor for a given region on the constant energy surface in phase space equals the volume swept out by that region as the total energy changes incrementally from ε to ε+dε. For a certain mode with high energy, the change in the corresponding coordinate and momenta necessary to increment the energy by de is less than for modes with low energy – just as the increase in speed needed to give a certain increase in kinetic energy is less for a particle that is already moving rapidly than for one that is moving slowly (because the kinetic energy is quadratic in speed). Therefore, the volume of phase space swept out near a high-energy mode on the energy surface is less than near a low-energy mode, so the weight factors are correspondingly less.

Classically it was assumed that every energy mode is capable of possessing any amount of energy, from zero to infinity, so the phase space was continuous and had no natural scale, which presents some subtle problems when trying to decide how to count states. However, following Planck, we could hypothesize that energy modes are actually capable only of possessing integer multiples of a certain fundamental irreducible quantum of energy, and we could suppose that this quantity depends on the frequency of the energy mode. The simplest supposition is that the energy ε of a mode with frequency ν can only take on one of the discrete values

where h is a fundamental constant of nature (now called Planck’s constant). We still assert that the weight factors to be assigned to the energy levels are related according to the exponential formula (3), but we simply restrict the values of ε to the appropriate set of discrete values depending on the frequency.

The task now is to determine the mean value of energy for a mode with frequency n. Recall that if energy is treated continuously with the distribution (3) we get a mean value of kT for the energy, regardless of frequency. However, using the same exponential relation for the weight factors, but restricting the energy levels to the discrete values given by (4), the mean value of energy is

If ν is small, this approaches the continuous case, so the mean energy approaches kT, but for larger ν the weight factor for the n = 0 term (which is constant) begins to predominate over the weight factors for n > 0. The denominator can never be smaller than 1/kT, whereas the numerator goes to zero. Making use of the geometric series identities

we can evaluate the summations to give the mean energy level for the frequency ν

Multiplying this by the spectral density (1) gives Planck’s formula for the energy density per unit volume of cavity radiation as a function of frequency

This replaces the classical Rayleigh-Jeans law given by equation (2). A normalized plot of this function is shown below.

The usual derivation of Planck’s law, as described above, simply assumes that the Boltzmann distribution (3) gives the correct weight factors for discrete energy levels, even though that distribution was derived classically from the dynamics of a continuous distribution. There are actually several different classical derivations of Boltzmann’s distribution for various circumstances, but they all involve continuously distributed energy levels, and some of them explicitly rely on the continuity. For a discrete set of energy levels one might have expected, a priori, something like a Poisson distribution, and yet the normalized continuous exponential distribution, evaluated at discrete intervals, undeniably leads to excellent agreement with experiment. Can this agreement be explained, or, to put it another way, can we justify the use of the continuous Boltzmann distribution in determining the weight factors for discrete energy levels? One way of approaching this would be to recall that the permissible energy levels for each frequency are the eigenvalues of the energy operator, and measurements of the energy level correspond to the application of this operator to the state vector, yielding one of the discrete eigenvalues as the measured energy. However, the state vector (which determines the probabilities of the discrete eigenvalues) evolves continuously between interactions. It might be possible to show that the continuous probabilities encoded by the state vector (or, equivalently, the wave function) satisfy Boltzmann’s simple exponential distribution, and this is why the eigenvalues have weights given by that distribution.

Incidentally, we commented previously that, in a sense, quantum theory began with Democritus and the atomistic doctrine, but of course that doctrine was opposed by Aristotle, who argued for continuous matter. This seems to be a natural debate, since we tend to analyze the objects of our experience into their constituent parts, leading to the question of whether this analysis can continue indefinitely or whether we, at some point, reach non-zero irreducible elements. In this light, the ancient doubts (as in Zeno’s paradoxes of motion) over whether space and time (and therefore motion and momentum and energy) are continuous or discrete can be seen in retrospect as intuitions about the necessity of the quantum. From a more modern dynamical standpoint, the very existence of stable configurations of matter is sufficient to refute scale invariance. If all the forces of nature were (for example) of the inverse-square type, there would be no characteristic length, but there could also be no stable structures. Stability requires a balance between two or more inhomogeneous effects, and this automatically implies a characteristic length.

Return to MathPages Main Menu