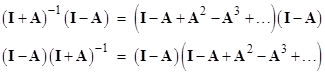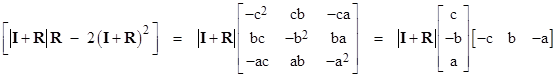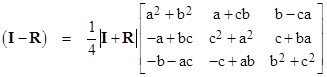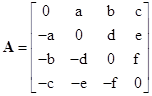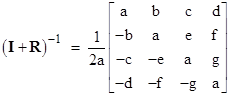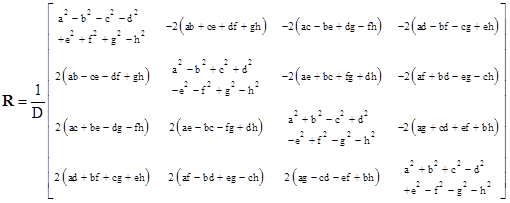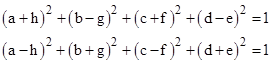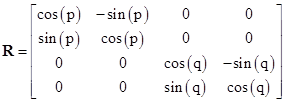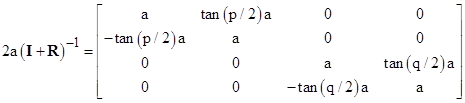Rotations and Anti-Symmetric Tensors

In a previous note we observed that a rotation matrix R in three dimensions can be derived from an expression of the form

and similarly in any other number of dimensions. The first matrix on the right side is simply the identity matrix I, and the second is a anti-symmetric matrix A (i.e., a matrix that equals the negative of its transpose). Thus we can write the above relation, for any number of dimensions as

 Solving for R, we get

There is no ambiguity in writing the right hand side as a ratio, because the matrices (I – A) and (I + A)^-1 commute, as shown by considering the two products (expanding the inverse matrix into the geometric series)

When the right hand sides are multiplied out, every term is a product of identity matrices and the A matrix, so the order is immaterial, and hence the two products are identical. To verify that, in fact, every matrix R expressible in the form (2) is a rotation, recall that a rotation (i.e., a special orthogonal transformation) is defined by the conditions

The first of these two conditions is nearly sufficient by itself because, since the determinants of a matrix and its transpose are equal, the first condition implies that |R| is either +1 or –1. Hence the second condition serves only to single out the positive sign of the determinant. To show that any R given by (2) is a rotation, we re-write that equation in the form

Taking the transpose of both sides, we get

Now, since A is anti-symmetric, it equals the negative of its transpose, so this equation can be written as

Multiplying both side of (3) on the right by the respective sides of this equation, we get

Multiplying both sides on the right and left by the inverses of I–A and I+A respectively, this becomes

where we have made use of the commutativity (as noted previously) of the factors on the right side. To prove that the determinant of R is +1 rather than –1, it suffices to observe that equation (3) gives the determinant +1 for R if A = 0, and by continuity it must be +1 for any other (real-valued) matrix A.

By equation (2) we have

which is known as Cayley’s transformation, and it can be inverted to give

We proved above that is A is anti-symmetric then R is a rotation. Conversely, if R is a rotation, then A is anti-symmetric. To prove this we need to show that A = −A^T. Negating the transpose of the above expression for A gives

Since (A^T)(A⁻¹)^T = (A⁻¹A)^T = I, we know that (A^T)⁻¹ = (A⁻¹)^T, so we have

Now, if R is a rotation we have R^T = R⁻¹, so we have

which proves that A is anti-symmetric. Consequently, we have a one-to-one mapping between rotations and anti-symmetric matrices. This applies to all rotations, including infinitesimal rotations, i.e., rotations of the form ρ = I + ε where ε is an infinitesimal anti-symmetric matrix, as confirmed by the fact that we can write ρ = (I + ε/2)/(I − ε/2).

In the previous note we also discussed a condition on rotation matrices that can be written as

where k is a constant depending on the number of dimensions of the space. We noted that in two dimensions the determinant of the matrix I - R is non-zero except for any rotations other than the identity, so it can be divided out of this equation, and we have k = 1 with the equality

For higher dimensions (at least for dimensions three and four) the determinant of I – R is identically zero. Hence we can only factor the relation as

In the case of three dimensions, the solution is given by setting k = 2, which results in the expression in square brackets reducing to

where the variables a,b,c are as defined for the three-dimension rotation given in (1), and

The other factor on the left side of (4) is

It is straightforward to verify that the product of this matrix and the matrix in the preceding equation is identically the zero matrix, which is to say, the rows of one are orthogonal to the columns of the other, and vice versa. We already noted that the determinant of I – R vanishes in more than two dimensions, but it’s interesting that the determinant of the second factor in (2) also vanishes, in three dimensions, provided we set k = 2. Letting f(z) denote the function

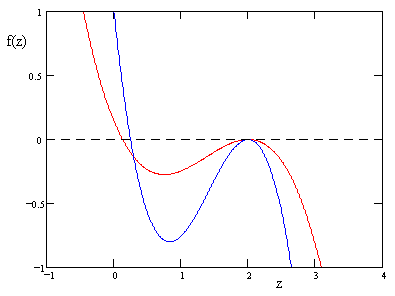
we can plot f(z) versus z for real values of z, as shown in the figure below for two arbitrarily chosen rotations in three dimensions.

In addition to the common repeated root at z = 2, the function f(z) for each three-dimensional rotation R also has another root at

as can be verified by direct substitution into f(z), then factoring out the |I + R|/4, and noting that

In four dimensions the general rotation can again be expressed as R = (I - A)(I + A)^-1, where now the matrices are of dimension four and the anti-symmetric matrix A is

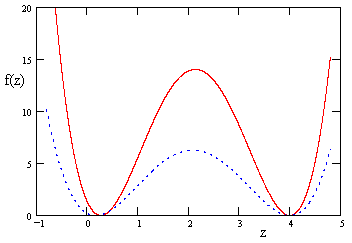
As discussed in the previous note, relation (4) is satisfied with k = 4, but only under the condition that af  – be + cd = 0. (See the note on Lorentz Boosts and the Electromagnetic Field for a comment on this condition.) Just as in the three-dimensional case, equation (4) is also satisfied by z = |I + R|/4, in addition to the general solution z = 4. In this case each of these represents a repeated root, as can be seen from the figure below, which shows f(z) for two rotations in four-dimensional space (each satisfying the special condition af – be + cd = 0).

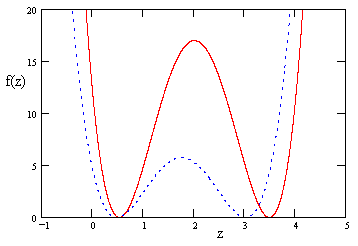
More generally, if we allow the quantity af – be + cd to be non-zero, we find that f(z) still has two repeated roots, although now there is no common solution with z = 4. Instead, both of the roots vary, as shown in the figure below for two arbitrarily selected rotations.

If we apply the homogeneous approach taken in the previous note (so now the symbols a through h are defined as in that note), we can define a fully general four-dimensional rotation matrix R by the relation

for constants a, b, c, d, e, f, g, and we then define the eighth parameter

We can now extend the 2-parameter expression in two dimensions and the 4-parameter expression in three dimensions to an 8-parameter expression in four dimensions, giving the completely general four-dimensional rotation matrix as

where

The eight parameters are constrained by the normalizing condition D=1, and by the relation

so there are six degrees of freedom, corresponding to the six “planes” in four dimensions (just as there are three degrees of freedom for rotations in three dimensions, and one degree of freedom for rotations in two dimensions). Adding and subtracting twice the second of these constraints from the first, we get the equivalent conditions

Thus for any specified values of b,c,d,e,f,g we can compute a+h and a−h, which gives the values of a and h.

We note that relation (4) with k=4 holds for four-dimensional rotations just if h = 0, which implies that bg – cf + de = 0. This corresponds to “simple” 4d rotations, i.e., those that can be expressed in the form

in a suitable system of rectangular coordinates. However, the most general 4-dimensional rotation actually consists of two such rotations, and can be written (in terms of a suitable system of coordinates) in the form

This can be written as a product of two simple rotations, but it is not a simple rotation in terms of any system of coordinates. To infer the “Euler parameters” for this rotation, we have

Thus we have the parameters a=a, b=tan(p/2)a, c=d=e=f=0, and g=tan(q/2)a. From this we find that h = tan(p/2)tan(q/2)a, which vanishes if either p or q is zero.

For a related discussion, see the article on Multiplying Rotations.

Return to MathPages Main Menu