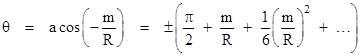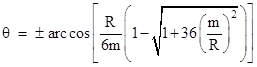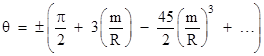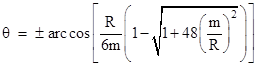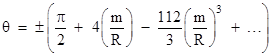Gerber’s Light Deflection

In another note we examined Paul Gerber’s theory of gravitation, which is often said to give (in the lowest approximation) the same formula as general relativity for the anomalous precession of planetary orbits. This apparent equivalence comes with a caveat though, because, as Roseveare points out in his 1982 book, Gerber’s formula doesn’t include the velocity-dependence of mass implicit in any viable theory of dynamics. Lacking any reason for excluding it, this effect, which adds 7 arcseconds per century to the perihelion precession of Mercury, must be added to Gerber’s formula, thereby destroying the agreement with observation. (In contrast, the effects of special relativity are already subsumed in the general relativistic derivation of the formula, so there is nothing to add.) Roseveare presents this as one of two empirical disproofs of Gerber’s theory.

The other is based on the deflection of light near a gravitating body. Making use of Gerber’s potential, and assuming a pulse of light follows the same path as a material particle with speed c, Roseveare presents a derivation that gives a deflection of 6m/R radians, where m is the mass of the gravitating body and R is the grazing radius of the light (both in geometrical units). Modern measurements in the visible and radio ranges of the spectrum show that the actual deflection is 4m/R, as predicted by general relativity. Thus, according to Roseveare, the deflection given by Gerber’s theory is too great by a factor of 3/2. However, this is based on the premise that the constant of motion h = r²(dθ/dt) for a pulse of light is infinite, which has no clear justification within Gerber’s theory. As is explained below, it is more consistent with Gerber’s theory to take a finite value of h, just as Soldner did when evaluating the Newtonian prediction for the deflection of light. On this basis, we find that Gerber’s theory actually predicts a deflection of 8m/R, which is twice the empirical value.

Any dynamical treatment of light in the context of Gerber’s theory – or any theory formulated in Galilean space and time – entails an ambiguity, because such theories are not directly compatible with any viable theory of light. For example, the Newtonian equation for the path of a test particle in a spherically symmetrical gravitational field is

where r = 1/u is the radial distance of the test particle from the gravitational source of mass m, and θ is the angular position of the particle, and h = r²(dθ/dt) is a constant of motion corresponding to the angular momentum of the particle. What does this equation imply about the path of a pulse of light? If we were to assume that light propagates instantaneously, then h is infinite, and the equation reduces to d²u/dθ² + u = 0, whose solution is u = cos(θ)/R where R is the distance between the particle and the gravitating mass at perigee.  This describes a straight line (viewed as a hyperbolic path, the asymptotes occur at u = 0, which is θ = ±π/2), so there is no deflection at all. But light is known to have a finite speed, so according to Newtonian concepts we ought to have a finite value of the constant h. It’s easy enough to assume (as Soldner did in 1804) that a light pulse has the speed c at the perigee, and hence we have h = cR. Choosing units so that c = 1, this is written as h = R, and equation (1) then has the solution (given by the sum of the homogeneous and particular solutions)

Again the asymptotes of this hyperbola are at u = 0, which occurs at the angles

The difference between these two angle exceeds p by the amount 2(m/R), so this is the amount of deflection predicted by the Newtonian formula – on the assumption that light behaves like an ordinary test particle with speed c at the perigee. However, according to this treatment, the pulse of light speeds up as it approaches the gravitating mass and slows down as it receeds from the mass, as can be seen by equating the changes in specific potential and kinetic energy as r ranges from the perigee R to infinity

In units with c_R = 1 this gives the asymptotic speed of the test particle as

Interestingly, the minimum perigee distance R corresponding to a real speed at infinity is the Schwarzschild radius 2m. In any case, the speed of light is clearly treated here as variable, whereas every observation indicates that light has a single characteristic speed regardless of its origin and past history. Hence neither of the possible assumptions about light (infinite speed or variable finite speed) are fully satisfactory, so the Newtonian prediction for light deflection is ambiguous, depending on which of these two unsatisfactory assumptions we make about the propagation of light.

More fundamentally, this ambiguity arises whenever we try to describe relativistic phenomena in terms of a Newtonian theory, because such theories do not distinguish between coordinate time and proper time, and in particular they do not recognize null paths through spacetime. In a Newtonian theory, if we decide to treat a pulse of light under the influence of gravity like a particle of matter that happens to be moving (at some particular instant) with the speed c, then this pulse has a finite angular momentum, which is constant over its entire trajectory (for a central force). Now, the constant of motion corresponding to angular momentum that arises in relativity is h = r²(dθ/dτ) where τ is the proper time along the path of the particle, whereas in a Newtonian theory such as Gerber’s the constant of motion is h = r²(dθ/dt) where t is the absolute coordinate time. When applying Gerber’s theory to a pulse of light, which of these expressions should we use? The difference is significant, because dτ along the path of light is zero, so h is taken to be infinite, whereas in Gerber’s theory the value of h for a particle moving with the speed c at the perigee a distance R from the center of the force is h = cR.

Roseveare’s derivation of light deflection in Gerber’s theory takes h equal to infinity, so he is choosing to adapt Gerber’s theory to special relativity, presumably in the same spirit that he contends we must add the special relativistic precession to Gerber’s orbital precession formula. This is an understandable approach, but some might argue that, since Gerber’s theory gives the correct precession if the special relativistic effect is not introduced, perhaps the theory somehow accounts for the effects of special relativity in a Galilean spacetime. To test this idea, we need to examine what Gerber’s theory predicts for the deflection of light in classical spacetime, i.e., treating a pulse of light as a Newtonian particle in Galilean space and time, with a finite value of h. On this basis, we will find that Gerber’s theory actually predicts a deflection of 8m/R, which is twice the empirical (and general relativistic) value. Thus it furnishes an even stronger refutation of Gerber’s model, and disposes of the idea that Gerber’s theory is consistent with observation, regardless of whether we apply it in the classical or the special relativistic context.

As derived in the previous note, the equation of motion arising from Gerber’s potential is

where u = 1/r, and h = r²(dθ/dt). This is equivalent to equation (6.35) in Roseveare. The value of h is constant, corresponding to the specific angular momentum of the particle. In the classical context of a small material particle on a hyperbolic trajectory, with velocity c = 1 (the speed of light) at a distance R from the center of the force, we have h = R, but at this point Roseveare says “To calculate the deflection of light we consider a particle approaching from infinity. For this we put h = −∞ …”. It’s unclear what this assignment of the value of h has to do with approaching from infinity, because h is a constant of motion, having the same value at every event on the trajectory. The actual justification for setting h to infinity, at least in the context of special relativity, is that the constant of motion is h = r²(dθ/dτ) where τ is the proper time along the path of the light pulse. Since dτ = 0 along a ray of light, it follows that h is infinite. Based on this premise, the term m/h² in equation (2) vanishes, leaving the differential equation

To derive an approximate solution of this equation, Roseveare treats the left hand side as the basic differential equation and the right hand side as the forcing function. The homogeneous equation

has the solution

Roseveare inserts this into the right hand side of (3) to give the forcing function

Now we define the “particular solution” u_p such that the left side of (3) equals this forcing function, i.e.,

The equation is satisfied by

Roseveare then combines the “homogeneous” and the “particular” solutions to give the total (approximate) solution

Of course, strictly speaking, this implies that the forcing function we used was not correct. We should substitute this new expression for u into the right hand side of (3) to give the new forcing function, and then determine the new particular solution, and so on. However, this would just provide higher order corrections. We already have the accuracy we need from the expression given above. (Roseveare doesn’t mention that this is just an approximations; he refers to it simply as “the solution” of (3).)

To infer the deflection angle from this solution, Roseveare reverts back to the r variable, and then transforms to x and y coordinates, from which he infers the deflection angle. A more direct approach is to simply note that the asymptotes of the hyperbola, where r goes to infinity, correspond to u = 0, so we need only determine the angles θ such that u = 0. Hence these angles are the solutions of

Solving this quadratic for cos(θ), and taking the inverse cosine, we get the angles of the two asymptotes

Expanding this to a series in the small quantity m/R, we get

The difference between these two angles is

which is the total arc swept out from one asymptote to the other. Subtracting π from this gives the total angular deflection as 6m/R (neglecting terms of higher order), which is the value reported by Roseveare, being 3/2 times the empirical value of 4m/R. However, as explained above, this was based on setting the value of the constant h to −∞, which is somewhat incongruous with the pre-relativistic foundations of Gerber’s theory.

Now we will repeat the derivation, but this time without introducing any special relativistic features. As noted above, the pre-relativistic value of h for a hyperbolic orbit, for a speed of 1 at the perigee distance R, is simply h = R. Therefore, substituting this value into (2), the equation to be solved is

rather than (3). The “homogeneous equation” is the same, so we still have uh = cos(θ)/R, but substituting this into the right hand side of (4), we see that the “forcing function” must include the constant m/R², so the “particular solution” u_p must satisfy

Hence the particular solution is

and the total solution is

Again, the angles of the asymptotes are such that u = 0, so they satisfy the equation

Proceeding just as before, we solve this quadratic for cos(θ) and take the inverse cosine to give the angles of the two asymptotes

Expanding this to a series in the small quantity m/R, we get

The difference between these two angles is

which is the total arc between the two asymptotes. Subtracting π from this gives the total angular deflection as 8m/R (neglecting terms of higher order). This is 4/3 times the value computed by Roseveare with special relativistic assumptions, and hence twice the empirical value of 4m/R.

Return to MathPages Main Menu