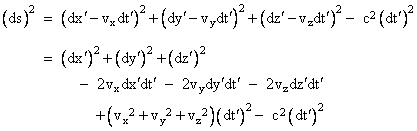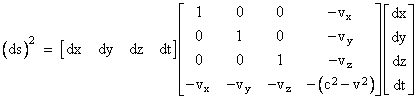Acoustic Metrics and the Vacuum

The metrical line element for Euclidean space, in terms of Cartesian coordinates, is

The quantity ds is taken to represent the incremental “distance” corresponding to the coordinate increments dx, dy, and dz. The justification for assigning special significance to this sum of squares is that it is invariant under the natural symmetries of space (according to our intuitive conception of space). For example, if we shift the origin of the coordinate system, thereby offsetting each of the coordinates x,y,z by some fixed amounts, the differentials are unaffected, so the distances along any specified path are unchanged. Furthermore, if we subject the coordinate system to a rotation, it can be shown that the expression (1) remains unaffected.

Now, consider a class of entities that moves through space, in time, at a definite characteristic speed c. Thus we have the relation ds = cdt, which signifies that the incremental times dt of such an entity are related to the corresponding incremental spatial components dx, dy, dz by

If the speed c is a constant, this equation is simply a re-scaled version of the spatial metric, so for this class of entities (i.e., entities that always propagate through space in time at the speed c) the quantity dt is seemingly just as suitable as the quantity ds as a definition of “distance”.

One of the definitions of a straight line in geometry is a locus of points from one given point to another that minimizes the total integrated “distance”. This definition, combined with the spatial metric (1) implies that a straight line is described by a linear function of the coordinates x, y, z. Similarly, one of the principles of physics is that a free entity moves through space in time from one given point to another in such a way as to minimize the time. (This is Fermat’s principle of least time.) Combining this principle with the temporal metric (2) leads to the conclusion that the c-speed entities travel in straight lines. Hence if we adopt (2) as our definition of “distance”, we are essentially just defining the distance between two given points as the time required for a c-speed entity to travel from one to the other.

The temporal definition of distance given by (2) is most likely to be useful when dealing with entities that always move at some characteristic speed c in terms of the given system of coordinates. Ordinary material particles can move at many different speeds, depending on the forces to which they are subjected, so no single value of c would be suitable. On the other hand, acoustic waves (i.e., sound waves) ordinarily propagate through a given medium at a fixed characteristic speed relative to the medium. Therefore, for purposes of describing and analyzing the behavior of acoustic disturbances in a medium, it is often convenient to use the acoustic metric defined by (2). Of course, this form is valid only if the medium is at rest in terms of the x,y,z,t coordinates, and only if the speed of sound is isotropic, i.e., the same in all directions.

However, it is not necessary for the value of c to be the same at every location. For example, the speed of sound at any given point in a gaseous medium depends on the temperature of the gas at that point, and this may vary from place to place. Hence the value of c in the acoustic metric (2) may be a function of the coordinates x,y,z.  In such a case, the metrical space is no longer Euclidean. Applying Fermat’s principle of least time, we will find that acoustic rays propagate along curved paths through the geometrical space. This is as one would expect, since a wave front propagating through a region in which the speed of propagation varies along the front will progress faster at some points of the front than at others, and hence the wave front will tilt, and the wave will be diverted. This corresponds to the curving of the acoustic rays.

At this point we should note that equation (1) represents the metric for three-dimensional Euclidean space, and equation (2) is written in the same form, treating time as the “distance” function for spatial relations. If we limit our considerations exclusively to entities that travel at the speed c, and if we were only concerned with measurements along the paths of individual entities, this would be adequate. However, in general we are interested in measuring the “distance” between entities at arbitrary times and places, such as the simultaneous spatial distance between two entities. It is somewhat inconsistent to use the temporal metric (2) to represent such distances, because that metric actually represents the “distance” between two spatial locations at two different times. An entity traveling at the speed c departs from one location at a certain time and arrives at another location at a later time, and we are using the elapsed time as a measure of the “distance” between the two locations, but it is really the “distance” between two events, namely, the departure at one time and place, and the arrival at another time and place. For a complete metric we actually need some way of assigning a physically meaningful “distance” between two events in the four-dimensional manifold of space and time.

Recall that our justification for identifying the sum of squares of the coordinate differentials as the physically meaningful definition of distance in Euclidean space was based on the presumed physical symmetries. The expression for ds is chosen because it is invariant under coordinate transformations (displacements and rotations) that represent the physical symmetries of space. This leads us to ask what are the relevant physical symmetries for our space-time manifold, based on the propagation of acoustic waves. Naturally we require symmetry under displacements and spatial rotations, but with the introduction of the time coordinate we need some additional symmetry to characterize intervals in space-time. In 1887 Voigt noted that the form of the simple wave equation

is invariant under what we would now call (up to a constant factor) a Lorentz transformation of the space and time coordinates

where v is the speed (in the x direction) of the accented coordinates relative to the original coordinates, and  γ = [1-(v/c)²]^-1/2. Thus if we wish to found a system of measure on the propagation of acoustic waves, we will find it most convenient to define our measure of absolute “distance” between events in a way that is invariant under this class of transformations (as well as displacements and rotations). Under such a transformation the line element

is invariant. Comparing this with equation (2), we see that ds = 0 along a propagating wave. Bear in mind that the symbol “c” here denotes the speed of sound in the medium.

So far we’ve considered the acoustic metric only for coordinates in terms of which the medium of propagation is at rest, but we can easily extend the concept of an acoustic metric to include the effects of motion of the medium. Letting v_x, v_y, v_z denote the components of the velocity of the medium at a given point relative to the coordinates x’, y’, z’, we know these are related to the original coordinates x,y,z (in terms of which the medium is at rest) by the Galilean transformation

Substituting for dx, dy, and dz in equation (4), we get

Re-arranging terms and simplifying, we get

Dropping the accent symbols, this can be written in matrix form as

Bear in mind that c and the components of v are both allowed to be functions of the time and place. Together these represent the effective speed of propagation of the acoustic rays relative to the chosen system of coordinates. An equivalent way of writing this metric is by using index notation and identifying the variables x,y,z,t with the super-scripted symbols x¹, x², x³, x⁴ respectively. With this notation we can write the acoustic metric in the form

where summation from 1 to 4 is implied over each repeated index, and the metric tensor g_mn equals the square matrix in the preceding expression. Writing the acoustic metric in this notation emphasizes the formal similarity with the metric of Riemannian geometry, although we must keep in mind that the quantity “ds” here has a somewhat convoluted meaning. The form of the expression for ds in terms of the original coordinate system was based on the invariance of that expression under the acoustic Lorentz transformation, but when we subsequently transformed the expression to a relatively moving system of coordinates we applied the Galilean transformation. Had we applied the acoustic Lorentz transformation to the original Minkowski metric, the result would have been again the Minkowski metric. We arrived at the above non-trivial acoustic metric only by first defining ds as invariant under the Lorentz transformation, and then applying a Galilean transformation to it. This interplay between two different systems of measure, two different concepts of distance, one designed to conform to a specific acoustic wave propagation, and the other consisting of the fundamental “true” measures of spatial and temporal intervals.

This dichotomy is present in some cases even when the “acoustic metric” is based on the propagation of light waves. An example of this is the propagation of light in a medium of varying refractive index. Recall that the index of refraction is simply a measure of the speed of light in a medium, and it varies as a function of the density. If the density of a transparent substance varies from place to place, rays of light passing through that substance will “bend” in accord with Fermat’s principle of least time using the metric (2), with c equal to the speed of light at each point. Since the speed of light in a refracting medium is less than the speed of light in vacuum, there is still a difference in this case between the “light metric” and the “true” measures of space and time.

This dichotomy vanishes only when the wave propagation metric is based on the propagation of light in vacuum. In this case, the “acoustic metric” and the “true” metric coincide. To understand this, note that all waves propagate through some medium at a characteristic speed relative to the medium. This is as true for electromagnetic waves in the vacuum as it is for sound waves in a material medium. Of course, the meaning of “speed relative to the medium” is ambiguous when the “medium” is the vacuum, because we have no definite way of determining the rest frame of the vacuum. Indeed, it can be argued that this is true by definition, because if we are able to assign a definite state of motion or rest to some entity, we classify that entity as substantial, whereas the vacuum is by definition the absence of all substantial entities. This is why waves in a vacuum (i.e., massless disturbances) are usually considered to be more fundamental than acoustical waves in a material medium. In fact, the seemingly continuous media of our common experience – such as ordinary gases, liquids, and solids – actually consist (on the microscopic level) of mostly vacuum, with huge numbers of elementary particles interacting via electromagnetic forces through the vacuum. Hence the acoustic (sound) waves of our common experience are actually an emergent phenomenon, arising from the more fundamental electromagnetic interactions.

The fundamental measures of space and time are represented by inertial coordinate systems, defined such that mechanical inertia is explicitly both homogeneous and isotropic. We have no more fundamental phenomena on which to base the definitions of space and time intervals than the phenomena of inertia. This basis was made even more secure by the recognition that all forms of energy – including light waves – possess inertia. Light propagates in vacuum, so the inertia of light and the wave propagation of light are both isotropic with respect to the same systems of coordinates. Therefore, the “acoustic metric” based on the propagation of light waves in vacuum is identical to the Minkowski metric of spacetime when expressed in terms of any system of inertial coordinates, and the appropriate symmetry corresponds to Lorentz transformations with parameter c equal to the invariant speed of light in vacuum.

Of course, in general relativity we again encounter line elements of the form

with some non-trivial metric tensors, but in this context the variation of the metric tensor is not due to inconsistent transformations (as it is for acoustic metrics), but rather to the intrinsic curvature of the space-time manifold itself. At least, this is the account given by the geometric interpretation of general relativity. Some prominent physicists have occasionally speculated on the possibility that the metrical relations of spacetime in general relativity actually are emergent from some underlying structure, somewhat in the same spirit as hidden-variable theories of quantum mechanics. However, no structure underlying the vacuum of spacetime has ever been detected. It is certainly true that the vacuum possesses properties, but none that enable us to assign a definite state of motion or rest to the vacuum.

Return to MathPages Main Menu