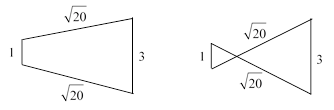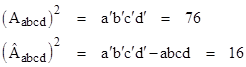Quadrilateral Duality

I could at first see no stars from the chaise-cart. But they twinkled out one by one, without throwing any light on the questions why on earth I was going to play at Miss Havisham's, and what on earth I was expected to play at.

                                                                               Charles Dickens

In the note on areas of conic quadrilaterals we saw that the net area of a quadrilateral inscribed in a conic section can be expressed in terms of the generalized “lengths” of the edges, with the same characteristic as the inscribing conic. The generalized length of the edge between two vertices x_i,y_i and x_j,y_j is

where α,β,γ are specified constants. The area A of a suitably inscribed quadrilateral with generalized edge lengths a,b,c,d is

With the usual “circular” definition of length, corresponding to α = γ = 1 and β = 0, this is simply Brahmagupta’s well-known formula for the area of a cyclic quadrilateral (i.e., a quadrilateral inscribed in a circle). The previous note explained how this generalized formula applies to quadrilaterals inscribed in any conic section, using the appropriate generalized length function. We also commented briefly on the set of distinct inscribed quadrilaterals for a given set of edge lengths, and we noted the algebraic ambiguity in the signs of the edge lengths, which leads to either of two expressions for the net area, one representing the area of all the quadrilaterals without crossing edges, and the other representing the area of the quadrilaterals with crossing edges.

For convenience, given any set of four positive real numbers a,b,c,d as the generalized edge lengths, we can define the dual set of four numbers a′,b′,c′,d′ as follows

This relationship is reciprocal, i.e., we have

To simplify the expressions in what follows, we will focus on the circular case, so we can omit the discriminant (although our results apply for arbitrary conic sections by just re-inserting the appropriate discriminant). Using a “hat” to denote the area of a quadrilateral with crossed edges, we saw in the previous note that

By reciprocity we can also express the areas of the quadrilaterals with the dual edge lengths a′,b′,c′,d′ as

An immediate corollary of these area formulas is

Since the squared areas for the crossed quadrilaterals are the negatives of each other, one of them must be negative (unless both are zero), which implies that one of the areas is imaginary. To illustrate, consider the specific example depicted below.

These quadrilaterals can be inscribed in a circle, and they each have the edge lengths

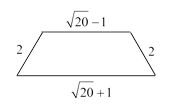
The dual edge lengths are

and in terms of these values we have the squared net areas

Recall that the net area is found by proceeding around the perimeter and considering the area enclosed by clockwise paths as positive and counter-clockwise paths as negative. It’s easy to confirm by direct inspection that the net areas of those quadrilaterals is

Now we consider the quadrilaterals with the dual edge lengths a′,b′,c′,d′. The un-crossed quadrilateral (which can be inscribed in a circle) is easy to picture, as shown below.

The squared net area is given by

and again it’s easy to verify by direct that the area is indeed

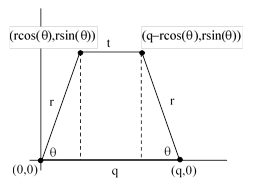
However, the crossed quadrilateral (that can be inscribed in a circle) in this case is not so easy to visualize. Given a quadrilateral with the sequence of edge lengths q,r,t,r the requirement for the vertices to be on a circle is equivalent to the requirement of the axial symmetry as shown in the figure below.

This implies that the angles denoted by θ must be equal and such that

If the right hand side is +t, we get the uncrossed quadrilateral as shown, but if the right hand side is –t the edges of length r cross each other, and we get the crossed quadrilateral with the same edge lengths (in terms of their magnitudes). This accords with the fact that we must take an odd number of the edge lengths as negative when applying the area formula, as discussed in the previous note. Using the well known formula for the net area of a polygon in terms of the coordinates of the vertices, the area of this quadrilateral is

The two values of cos(θ) that satisfy the cyclic condition are

If this value is in the range from −1 to +1 then the angle θ is real, but this equation can be solved for any values of q, r, and t, provided we are willing to accept complex angles. In our example with positive t we have

which leads to

Inserting these values into the area formula in terms of the vertex coordinates gives

in agreement with the edge length formula for the uncrossed quadrilateral. But what about the crossed quadrilateral, for which the edge length formula gives a squared area of −16, meaning the area must have the imaginary value 4i? For this case we take the negative value of t, which leads to

Hence the vertex coordinates are complex. Inserting these values into the area formula in terms of the vertex coordinates gives

in agreement with the edge length formula for the crossed quadrilateral.

We set two of the edge lengths equal to each other in the above example to simplify the calculations, and we also chose lengths that give real vertex coordinates for at least some of the quadrilaterals, but in general given any four real numbers we can consider the (possibly complex) quadrilaterals with those edge lengths, parameterized by the angle between two adjacent edges. We can place one of those edges on the x axis with one vertex at the origin, and then the adjacent edge is positioned with the angle parameter, so we immediately have the coordinates of the three of the vertices as a function of the angle. We can then locate the fourth vertex as one of the two points of intersection between circles centered on the outer vertices with radii equal to the remaining two edge lengths. Notice that, even of the edge lengths don’t satisfy the triangle inequality, so they have no real intersection, we can solve for the complex intersections. This gives us the coordinates of all four vertices of the (possibly complex) quadrilateral in terms of the angle parameter, which can then be varied to locate the two fundamental angles for which all four vertices lie on a circle. Hence the area formulas apply to set of four numbers, as well as to their duals.

Return to MathPages Main Menu