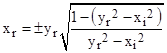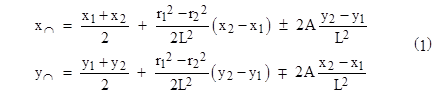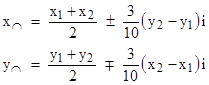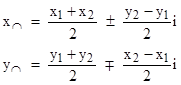Intersecting Circles

The bonds that unite another person to ourself exist only in our mind.

                                                                                Marcel Proust

A “circle” is ordinarily defined as the locus of points (on a plane) equi-distant from a given point called the “center”. Algebraically, in terms of a system of Cartesian coordinates “x” and “y”, we typically express this by defining a circle as the locus of points with coordinates (x,y) such that

where (x₀,y₀) are the real coordinates of the center, and R is the real radius of the circle, i.e., the metrical distance from the center to each point of the circle. Usually we tacitly restrict our attention to points with purely real coordinates, but without this restriction the algebraic definition actually implies a more elaborate structure, consisting of all the “points” with complex coordinates that satisfy the above equation.

As an example, suppose the center of the circle is at the origin of the coordinates, so x₀ = y₀ = 0, and consider the set of complex numbers x = x_r + ix_i and y = y_r + iy_i that satisfy the equation

where R, x_r, x_i, y_r, y_i are all purely real-valued numbers. This implies

Obviously if the imaginary components of x and y are both zero, the left hand condition is automatically satisfied and the right hand condition reduces to the usual equation for a real circle centered on the origin. However, if we allow x_i and y_i to have non-zero values, we have solutions for all sets of values of x_r,y_r outside the original circle, i.e., such that the sum of the squares of x_r and y_r exceeds R². The locus of these solutions could be regarded as the algebraically complete “circle”.

To visualize a complete circle, we can solve the left hand condition for y_i, insert this into the right hand condition, and solve for x_r to give

If x_i = 0 this equation simply gives x as a function of y for an ordinary real circle. For any other given value of x_i this equation gives x_r as a function of y_r for lines of constant x_i. Since x_r must be real-valued, we know the values of y_r must lie within the range

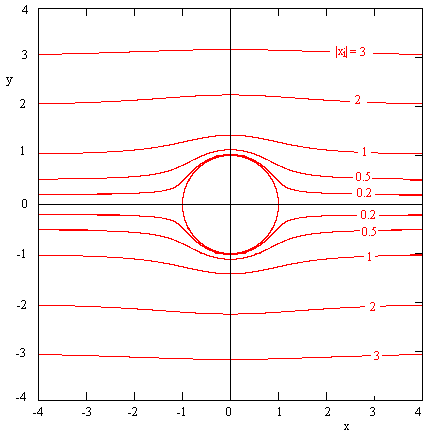
A plot of the lines of constant x_i for a circle of radius R = 1 is shown below. Note that since x_i appears only squared in the equation for these loci, they correspond to both positive and negative values of x_i.

As an aside, these contours are remarkably similar to the stream lines in potential fluid flow around a sphere or cylinder. A contour plot of the upper surface (i.e., the positive values of x_i) viewed from the side is shown below.

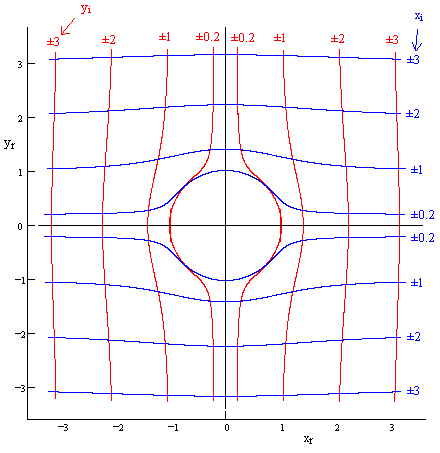
In the same way that we found the loci of constant x_i as a function of x_r and y_r, we can also solve for the loci of constant values of y_i, and by symmetry it is the same as those shown above, except rotated 90 degrees. Thus a complete depiction of an algebraically complete circle is as shown below.

In the three-dimensional space representing the coordinate components x_r, y_r, x_i, we see that an algebraically complete circle can be described as a double-covering surface that extends from the real circle out to infinity. Likewise in the space of x_r, y_r, y_i the circle is a double-covering surface. However, these two surfaces are not independent, because the relation x_rx_i + y_ry_i = 0 implies that the signs of x_i and y_i are linked. At any given point on the x_r,y_r plane, there are two possible values of x_i (of equal magnitude and opposite signs), and two possible values of y_i, but this doesn’t represent four possible combinations, because we have y_i = -(x_r/y_r)x_i. For example, if x_r/y_r is positive, then y_i and x_i must have opposite signs. Hence there are only two complex “points on the circle” for any given values of x_r and y_r. (Of course, these two “points” merge into one on the real circle, where the two parts of each surface meet.)

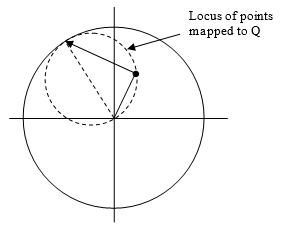
Incidentally, the flat “basin” inside the real circle (as depicted in the countour plot above) is the region where the computed value of x_i (and also y_i) would be imaginary, which means the value of x = x_r + ix_i and y = y_r + iy_i would be purely real. This implies that the resulting values of x and y are on the real circle, so the values of xi and yi are just such as to map each point (x_r,y_r) inside the circle to a point on the circle. Specifically, it maps the point (x_r,y_r) to the point with the coordinates

where r² = x_r² + y_r². It’s easy to verify that these points do indeed lie on the circle of radius R, and the second terms are perpendicular to the first terms, so it follows that each point inside the circle is mapped to the circle along the line perpendicular to the line from the center of the circle, as shown below.

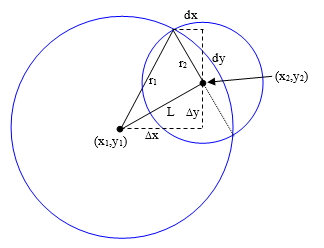
Now we consider the intersections between two circles, given the (purely real) radii and the coordinates of the centers. Let r₁ and r₂ denote the radii of the two circles, and let (x₁,y₁) and (x₂,y₂) denote the coordinates of their centers (in terms of a Cartesian coordinate system). For convenience we also let L denote the distance between the centers. It is straightforward to show that the intersection of these two circles consists of two points, with the coordinates

where A is the area of the triangle with edge lengths r₁, r₂, L, as given by Heron’s formula

As a simple example, consider two circles of radii 5 and 3 units respectively, with centers located a distance of 4 units apart, as depicted for a typical configuration in the figure below.

Since in this example we have r₁² – r₂² = L², the first two terms of the equations for the x and y coordinates of the intersection points are simply x₂ and y₂ respectively, so the equations reduce to

where we have put Δx = x₂ – x₁ and Δy = y₂ – y₁. Also, the area of the triangle with edge lengths L, r₁, r₂ in this case is simply Lr₂/2 (which can be confirmed by Heron’s formula), so we have

By similar triangles we have r₂/L = dx/Δy = dy/Δx, so we make these substitutions to arrive at the expected result

This merely confirms that equations (1) give the real intersection points for real circles that overlap in real space.

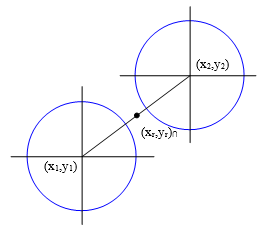
However, those equations also apply to any two circles, even if they don’t overlap in real space. For example, consider two identical circles, each of radius r₁ = r₂ = 2 units, with centers separated by a distance of L = 5 units.

These circles clearly have no real points of contact, but the algebraically complete circles do have two points of intersection in the full complex space. The area of the triangle with edge lengths 5,2,2 is imaginary, given by Heron’s formula as (15/4)i. Since r₁ = r₂, the second terms in equations (1) are zero, so the real parts of the coordinates of the intersection points are given by the first terms, which represents simply the midpoint between the centers of the circles. The imaginary parts of the intersection coordinates are proportional to the real components of the vector between the centers. For this example we have

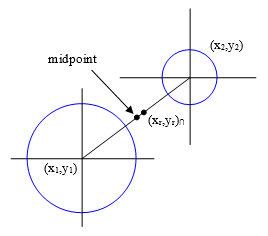
Thus if we rotate the configuration, keeping the radii and distance between centers the same, the vector between the centers rotates and the vector consisting of x_i and y_i rotates, but they are 90 degrees out of phase, since x_i is proportional to the y component of the vector between the centers, and y_i is proportional to the x component. The magnitude of the imaginary vector is a constant (2A/L)i. For a specific numerical example, suppose the centers of the two circles are located at (12,7) and (16,10). Inserting these values into the above equations, we get the coordinates of the two points of intersection

It can easily be confirmed that each of these points is a distance from 2 units from each of the centers.

If the radii of the circles are unequal, the real parts of x_∩ and y_∩ are no longer at the mid-point between the centers, but it still falls on the line between the centers, shifted toward the smaller circle. For example, if the radius of the second circle in the preceding figure was reduced from 2 units to just 1, the real parts of the intersection coordinates would shift from the midpoint (14, 17/2) to (14 + 12/50, 17/2 + 9/50) as shown below.

It’s interesting to consider the case when the radii of the circles shrink toward zero, in which case the area approaches A = (L²/4)i and the coordinates of the points of intersection approach

In this limiting case the squared distances from the origin of the coordinate system to these two intersection points are

Hence if we let d₁ and d₂ denote the distances from the origin to the centers of the (vanishingly small) circles, and if we let δ₁ and δ₂ denote the distances from the origin to the points of intersection of those circles, we have δ₁δ₂ = d₁d₂.

Return to MathPages Main Menu