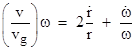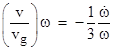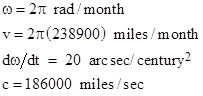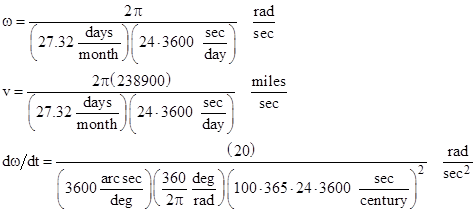Laplace on the Speed of Gravity

Ce que nous connaissons est peu de chose, ce que nous ignorons est immense.

                                    Pierre-Simon Laplace

By examining the reports of eclipse observations from antiquity to his own time, Edmund Halley in 1693 found evidence that the angular velocity of the Moon has been steadily increasing, at least over the last few thousand years. One possible cause of this (he thought) would be if space was filled with a tenuous ether, that might also serve as the medium for the propagation of light. The drag induced by this ether would cause the Moon to lose angular momentum and drop to a lower orbit with increased angular velocity, explaining why the period of the Moon’s orbit appears to be getting shorter. In 1695 Halley presented a paper to the Royal Society entitled “Concerning the Motion of Light” in which he discussed this possibility, and he mentioned that ancient eclipse observations lend support to the idea that indeed the Moon has undergone a secular (long term) acceleration, meaning that the lunar month (the time it takes the Moon to complete one orbit around the Earth) is appreciably shorter than it was thousands of year ago when the Babylonians made their observations. Incidentally, by extrapolating this effect into the future, one could foresee a time when the Moon crashes into the Earth, bringing the end of the world, a fact which Halley tried to use to defend himself against the charge that he believed – contrary to scripture – that the principles of science imply an eternal world.

When Halley’s friend Isaac Newton published the second edition of Principia in 1713 there appeared at the end of the discussion of Proposition 42 in Book 3 a brief mention of this interesting discovery:

And by combining the eclipse observations of the Babylonians with Albategeni’s and with today’s, our Halley showed that the mean motion of the Moon when compared with the diurnal motion of the Earth, gradually accelerates, as far as I know the first of all to have discovered it.

This comment was appended to a discussion of how comets might sometimes fall into the Sun, and how the tails of comets may impinge on the planets. In the latter case, the accreted material could slowly increase the masses of the planets, and this increase might have secular effects on the orbits of their satellites. Perhaps this is what Newton had in mind when he decided to mention Halley’s discovery in that section, since an increase in the Earth’s mass (while holding the Moon’s angular momentum constant) would correspond with a lower orbit and increased angular velocity. However, Newton was careful to say that Halley’s observed acceleration of the Moon was relative to the diurnal motion of the Earth, i.e., to the Earth’s rotation, from which we get our calendar days. Thus Newton realized that the observations could also be explained by a slowing of the Earth’s rotation, or by a combination of changes in the Earth’s rotation rate and the orbital speed of the Moon. Curiously, the reference to Halley’s discovery was deleted from the 3rd edition of Principia, so it’s not to be found in any of the widely available English translations today. The reason for its deletion is not known, but perhaps Newton decided it was too speculative for a discussion of matter accretion from comets.

The first quantitative estimate of the Moon’s apparent secular acceleration was made in 1749 by Richard Dunthorne, who arrived at the value 10″ (i.e., 10 arc seconds) per century. By this he meant that the Moon would gain 10″ on its expected angular position after one century. Since the effect is a cumulative increase in angular speed, after two centuries the Moon’s angular position has gained 40″, and after three centuries it has gained 90″, and so on. Thus the instantaneous angular acceleration is α = 20 arcseconds/century², and the Moon’s advance after T centuries is (1/2)αT².

Halley’s idea of a luminiferous ether as the cause of the apparent secular acceleration of the Moon was never widely accepted, and in the latter part of the 18th century several attempts were made to give a more satisfactory explanation. Several times the Academy of France offered a prize for the solution of this puzzle. By 1770 Euler declared that it couldn’t be explained on the basis of Newtonian gravity. Lagrange too tried and failed to find an explanation. This was the state of affairs when Laplace took up the problem around 1774. In what appeared to be another triumph for Newton’s theory, Laplace offered an explanation (first published in 1776) that seemed consistent with the data. He showed that the Earth’s elliptical orbit is gradually becoming more circular due to interactions with the other planets, and as a result the mean distance from the Sun is increasing slightly. In the three-body system consisting of the Sun, Moon, and Earth, the Sun has the effect of perturbing the Moon away from the Earth, but as the mean distance to the Sun increases, this effect is reduced, and hence the Moon orbits closer to the Earth and it’s angular velocity increases. Laplace supplied a calculation that seemed to give an advance of 10” per century, in remarkably good agreement with the value derived from observations.

Despite this seeming success, Laplace also considered other possible explanations. Among these was the possibility that the secular acceleration might be caused by a finite propagation speed of gravity. Although Newtonian gravity was conventionally assumed to extend instantaneously to all distances, Laplace commented that it would be more natural for it to propagate from place to place in some finite time, consistent with the propagation of other physical effects, such as light. To have escaped notice, the propagation time for gravity is certainly very slight, but Laplace remarked that “it is infinitely far from an unobservable time of propagation to one that is absolutely nil”. He gave an analysis of the possible effects of a finite propagation speed for gravity in a memoir (“Sur le principe de la gravitation universelle, et sur les inegalites seculaires des planetes qui en dependent”) published in 1776, and many years later included this discussion in Volume IV, Book X, Chapter VII of his Traite de Mecanique Celeste. There he wrote in paragraph 22

If gravitation be produced by the impulse of a fluid directed towards the centre of the attracting body, the preceding analysis… will give the secular equation depending on the successive transmission of the attractive force.

What Laplace refers to as the “secular equation” (as rendered in Nathaniel Bowditch’s English translation) is simply the term representing the secular acceleration in the expression for the angular position of the attracted body (i.e., the satellite). Laplace’s equation 9027 gives what he says is the “secular equation of the attracted body due to the successive transmission of gravity” for a satellite in a nearly circular orbit

where t is time, n is the mean angular velocity of the satellite at t = 0, and i is “the ratio of the velocity of the fluid which causes the gravitation to that of the attracted body”. Thus letting v and v_g denote the velocity of the satellite and of the in-flowing gravitational particles respectively we have i = v_g/v. Laplace goes on to give an expression for the speed of light in terms of the aberration of light from the Sun to the Earth, but since we now have independent measures of the speed of light, we needn’t bother with that. Of course, the mean angular position of the satellite is simply nt, and there is also a periodic term which we omit because it has no long-term cumulative effect, so Laplace’s equation for the angular position of a single satellite orbiting a gravitating body is

The derivatives of this give the angular velocity and the angular acceleration

Recalling that ω = 2π/P where P is the period of the orbit, it follows that dω/dt = -(2π/P²)dP/dt, and hence the equation for the angular acceleration can be written as

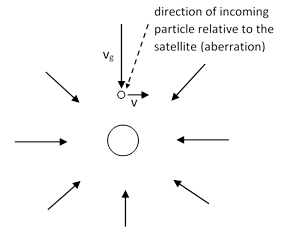
Notice that this is negative, meaning that the period is getting shorter, consistent with Halley’s observation. As discussed above, this corresponds to a reduction in angular momentum and a reduction in the orbital radius. In this hypothetical model the loss of angular momentum is due to the drag resulting from aberration of the incoming gravitational particles encountered by the orbiting satellite, as depicted in the figure below.

Just as a person running horizontally along the ground in a vertical rain will be hit in the face by rain drops, the satellite will encounter the incoming gravitational particles with a component tending to retard its motion, reducing its angular momentum. It’s worth emphasizing this, because many historical discussion of the Fatio/Le Sage “shadow” theory of gravity claim that Laplace’s calculation was relevant to that theory, whereas in fact the secular acceleration that Laplace was trying to explain was in the opposite direction from what would be expected from a finite speed of gravity in a shadow theory.

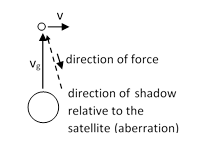
This is because, in a shadow theory, we do not have an ordered inward flux of particles all moving directly toward the center of the gravitating body (as in the case Laplace analyzed). Instead, the satellite is bombarded from all directions by an omni-directional flux of particles, and the net force on the satellite is due to the fact that there is a (very slight) deficiency in the intensity of the flux arriving from the direction of the gravitating body. Hence the net force is directed toward the stream of particles emanating from the central body, as depicted below.

Therefore, the finite speed of the posited gravitational particles in a shadow theory pulls the satellite forward, adding angular momentum, which (as discussed above) will tend to put the satellite into a higher orbit with a lower angular speed, exactly the opposite of the effect that Halley had reported and that Laplace was trying to explain. (Laplace discounted the possibility that the Earth’s rotation rate was slowing down.)

It’s relatively simple to derive the effect of aberration on a satellite in a two-body system for these mechanistic models of gravity, assuming the orbital changes are so slow that the orbit is very nearly circular at all times. First, note that the entire aberration angle for any circular two-body system is proportional to v/v_g where v is the sum of the tangential speeds (in opposite directions) of the two mutually orbiting bodies about their center of mass. This accounts for both the changes in positions and the Bradley effect. It’s important to be clear about this, because one sometimes sees descriptions of aberration that focus exclusively on the directions to the retarded positions of the objects, without also accounting for the Bradley effect. Admittedly the entire aberration can be seen as purely an effect of retarded position or as purely a Bradley effect, or a combination of the two, depending on the frame of reference, but we must not overlook either effect when using the frame of reference of the center of mass for a system consisting of two comparable masses. For simplicity, we will consider the case of a tiny satellite orbiting a large mass, so nearly all the relative velocity is the velocity of the satellite relative to the center of mass of the system.

Now, the nominal centripetal acceleration of a satellite moving with speed v on a circular path of radius r is v²/r = ω²r. This represents the inward radial force per unit mass on the satellite. It follows that the tangential force per unit mass due to aberration is (v/v_g)ω²r. To assess the rate at which this tangential force increases the angular momentum of the satellite, note that if r was constant the angular acceleration would be just the tangential acceleration divided by r, so we would have dω/dt = (v/v_g)ω². Also, recall that the specific angular momentum of a particle in circular motion of constant radius r and angular speed ω is L = ωr², so at constant r the aberration (for a shadow theory) would increase the angular momentum of the satellite at the rate dL/dt = (v/v_g)ω²r². Of course, in the actual case, r is not constant, but this expression still represents the rate of increase of angular momentum produced by the tangential force. Setting this equal to the full derivative of L with variable r, and dividing through by ωr², we get

We now invoke Kepler’s third law for circular orbits ω²r³ = M where M is the mass of the main gravitating body. (We are using geometrical units such that G = c = 1.) To determine how r and ω change as the orbit evolves from one circular Keplerian orbit to another (remembering our circularizing assumptions), we differentiate Kepler’s law to give

Plugging this into the preceding equation, we have

Since the orbital period P is related to ω by P = 2π/ω , we have  and hence the above equation can also be written in the equivalent form

As expected, this is identical to Laplace’s equation for the secular acceleration, but with the opposite sign, because this is for a shadow theory, whereas Laplace was analyzing a direct impulse “sink” theory. Re-arranging this relation in terms of ω, we have

where the sign depends on whether we are modeling a sink theory (as in Laplace’s memoir) or a shadow theory (as in Le Sage’s theory). The values of the parameters on the right hand side are

Converting these to a common set of units, we write

Plugging these values into the preceding equation gives the result

consistent with Laplace’s claim that of the fluid producing gravitation will be about seven millions of times greater than that of light”. (In a footnote, Bowditch carried out the numerical calculation indicated by Laplace, and confirmed that it “exceeds seven millions”.) Laplace went on to say

As it is certain that the Moon’s secular equation depends almost wholly on the cause we have assigned in the sixth book [i.e., the diminution of the eccentricity of the Earth’s orbit, and corresponding increase in the mean distance to the Sun], we must suppose that the gravitating fluid has a velocity which is at least a hundred millions of times greater than that of light; or at least we must suppose, in its action on the Moon, that it has at least that velocity to counteract her gravity towards the Earth. Therefore mathematicians may suppose, as they have heretofore done, that the velocity of the gravitating fluid is infinite.

Ironically, Laplace’s confidence in the explanation based on diminution of the Earth’s orbital eccentricity turned out to be misplaced. In 1853 John Coach Adams found an error in Laplace’s calculation, and when this was corrected the remaining prediction was only about half the size of Halley’s observed acceleration. Moreover, it is now known that the Moon’s orbit, in absolute terms, is actually slowing down (with a corresponding secular increase in the orbital radius – a few centimeters each year), just the opposite of what Halley had “observed”. The tidal interaction between the Moon and the Earth’s oceans has the effect of increasing the Moon’s orbital angular momentum. As a result, the Moon is gradually moving further away with a lesser angular velocity when measured in absolute terms. Nevertheless, Halley was correct that the calendar time for one lunar orbit is decreasing, but this is because the length of a calendar day is increasing. Just as the tidal interaction is adding angular momentum to the Moon, it is reducing the Earth’s angular momentum, and hence slowing the Earth’s rate of rotation, causing the appearance of an increase in the Moon’s angular velocity due to the lengthening of the days.

It was thought at one time (in the early 20th century) that the viscous drag of the oceans on the Earth could not account for the necessary transfer of angular momentum through tidal forces, but an analysis by Geoffrey Taylor in 1919 showed that the transfer is concentrated in locations of relatively shallow water and strong tidal currents. In fact, although the whole Pacific ocean contributes only a small amount, the Bering Sea produces nearly half of the total torque on the Earth arising from the tidal interaction with the Moon. Other areas of strong tidal activity, like the Irish Sea and the Gulf of Tonkin are also significant contributors.

Since the Moon’s orbital motions are (now) well explained by Newton’s theory of gravity, which assumes instantaneous propagation, there is presently no unexplained secular acceleration or deceleration, at least to the limits of observational precision, so the aberration argument of Laplace now implies an even greater lower bound on the speed of gravitational propagation for a mechanistic particle theory. For example, Poincare calculated that the gravitational particles in a Lesage theory would have to propagate with a speed at least 10¹⁷ times the speed of light. Of course, as Poincare noted, the kinetic energy imparted by the bombardment of such particles would vaporize the Earth in a fraction of a second, which is one of the (many) reasons that such mechanistic theories of gravity are not viable. In modern relativistic field theories (such as general relativity) the “forces” propagate at the speed of light, and the aberration effects are almost entirely absent because the “forces” are not purely central and the material entities are not the sole carriers of energy and momentum. The field itself contains energy and momentum flows, as needed to be consistent both with relativity and with the conservations laws. Indeed this “vanishing of the covariant divergence” is the defining property of relativistic field laws. Hence the analysis of Laplace, in which all momentum is concentrated in the material objects, is not applicable. Still, it’s interesting from a historical perspective to see how physicists and astronomers responded to the apparent secular acceleration of the Moon, and how the ancient Babylonian eclipse records affected the development of modern science. The ancient Greek astronomer Ptolemy (circa 140 AD) reportedly had access to Babylonian eclipse observations dating from the time of Nabonassar, who ruled about 747 BC. Today we have access to incredibly precise laser measurements bouncing off the mirrors left on the Moon by the Apollo astronauts in 1970 AD. These enable astronomers to determine the position of the Moon continuously within a fraction of a centimeter.

Amusingly, a supposedly reputable journal called Physics Letters A published a paper in 1998 in which Laplace’s analysis of aberration (for a theory in which the force of gravity is conveyed by an inward flux of material particles) was cited as “proof” that gravitation must propagate twenty billion times faster than light. Subsequently the journal published two rebuttal papers, both pointing out the well-known fact that a first-order torque does not arise in relativistic theories, as already demonstrated by (for example) the Trouton-Noble experiment. Neither of the rebuttal papers examined whether the original paper had correctly presented Laplace’s analysis on its own mechanistic Newtonian terms. For the record, the attempt to replicate Laplace’s 1776 analysis in the 1998 Physics Letters A paper was actually gibberish.

There are three numbered equations in that paper. The first is attributed to an introductory text on celestial mechanics (Danby, 1988), and we’re told it will be used later to compute a bound on the speed of gravity, but no connection is ever made between that equation and the one eventually used to compute the bound. The third numbered equation is simply Laplace’s well-known formula , which, as we’ve seen, is trivial to derive. However, the “derivation” of this equation presented in the Phys Lett A paper, which constitutes the paper’s only actual attempt at quantitative physical reasoning, is nonsense, even on its own terms, i.e., even in the context of a mechanistic central force with finite propagation speed.

The paper says its equation (3) is just a re-writing of its equation (2) “in a form suitable for comparison with observations”, but this is obviously false, because the paper’s equation (2) in our notation is . Now, if we let ω denote the angular velocity of the satellite with period P, we have P = 2π/ω, and we also know the velocity of the orbiting satellite is v = ωr, so the paper’s equation (2) is simply . Thus, where Laplace’s formula (equation 3 in the paper) has v/v_g, the Phys Lett A paper’s equation (2) has (1/3)(v/v_g)³, so equation (3) is obviously not a re-writing of equation (2) “in a more suitable form”. The two equations are completely incompatible. The one copied from Laplace and Danby makes sense, but the one “derived” in the Phys Lett A paper (which is claimed to be equivalent) is utterly absurd.

It’s easy to trace how the paper arrived at this nonsense. The “derivation” of equation (2) based on Figure 3 of the paper introduces the angle θ as the angular travel of the satellite in the time required for gravity to propagate. Thus θ is the aberration angle, essentially equal to v/v_g, which is the relevant ratio for determining the tangential acceleration of the satellite. But the Phys Lett A paper then introduces a different angle, called ψ, based on where the satellite would be if instead of moving on it’s circular path it proceeded in a straight line for the time required for gravity to propagate. This is completely senseless. The angle ψ has no relevance at all to the aberration angle, which is simply θ. Nevertheless, the Phys Lett A paper makes a meal of determining that ψ = θ – arctan(θ), and hence to the first approximation ψ = (1/3)θ³.  This angle is then plugged into a formula from Danby as if it was the aberration angle to arrive at equation (2).  (The paper refers to the coefficient “B” from Danby’s equation 11.5.13 without explanation, despite already using “B” to denote the central gravitating body.) This is why equation (2) has (1/3)(v/v_g)³ in place of v/v_g. Fortunately, after presenting this gibberish, the paper simply discards the result and adopts Laplace’s equation (3) under the guise of “re-writing” (2) in “a more suitable form”.

Thus the only actual attempt at quantitative physical reasoning contained in the paper is complete nonsense, even on its own 18th century mechanistic neo-Cartesian terms. How this paper passed peer review will be, I suspect, an eternal mystery.  This episode is at least mildly interesting (like the Sokal experiment) for the light it sheds on publication standards, and also perhaps on the psychiatric aspects of a certain kind of mentality. Failure to understand the absence of first-order aberration in relativistic theories is perhaps not too surprising, even for a purported “expert” on celestial mechanics, but  the inability of such a person (not to mention the Phys Lett A editors and referees) to distinguish sense from nonsense in a rudimentary derivation in Newtonian mechanics is rather remarkable.

As noted above, the two rebuttal papers in Phys Lett A (appearing in 1999 and 2000) made no comments on the original paper’s (blatently idiotic) attempt to reproduce Laplace’s analysis, and merely pointed out that relativistic forces (including both electromagnetism and gravity) involve velocity-dependent terms that almost exactly cancel the aberration effect arising from the finite speed of propagation. One of the papers correctly notes that the absence of torque in such situations is already demonstrated in the Trouton-Noble experiment, but it didn’t go on to mention that the fallacy of the original Phys Lett A paper was exactly the same as that of the well-known “Right Angle Lever Paradox”. The other rebuttal paper didn’t mention Trouton-Noble, and unfortunately suggested that the cancellation seems “miraculous”. Neither of the rebuttal papers directly addressed the actual root of the fallacy of the original paper, which was the belief that non-central velocity dependent terms “violate causality”, meaning essentially that they violate conservation of momentum, i.e., the same fallacy underlying the paradox of the Right Angle Lever.

It would have been helpful if the rebuttal papers had presented von Laue’s 1911 explanation of how momentum is explicitly conserved in such situations, rather than just presenting the cancellation as a mathematical artifact that seems like a miracle. The rebuttals mentioned only that radiation (dipole for electromagnetism and quadruple for gravity) carries momentum, but this corresponds only to the higher orders where aberration actually does appear. The original paper’s complaint, as emphasized in a follow-up paper responding to one of the rebuttals, was not related to those higher-order effects, it was that the first-order cancellation cannot be reconciled with causality and conservation of momentum. The momentum carried by the higher-order radiation does not answer this complaint. The real answer was already given by von Laue in 1911. He emphasized that since energy and work are frame dependent, any flow of energy also represents a flow of momentum, and not just in the form of radiation. In particular, a force applied to a stationary object does no work, but if viewed from a relatively moving system of coordinates the force is being applied through a distance, and hence does work. Any such work represents a flow of energy, and therefore also a flow of momentum. This insight enables us, in any particular physical situation, to explicitly identify the mechanisms and flows of energy/momentum relative to any specified frame of reference. For example, two electrically charged particles moving uniformly in oblique directions will result in varying electric and magnetic fields in their vicinity, and the Poynting vector S = E x B represents the energy flow at any point in space, and S/c represents the corresponding flow of momentum. The decomposition of an electromagnetic field into electric and magnetic components is frame dependent, and hence so is the flow of energy (just as when dealing with material entities). This is the causal mechanism by which the two charged particles interact, and we see that momentum is explicitly conserved everywhere, taking into account the flows of energy and momentum in the field itself. It’s crucial to recognize that these flow are not high-order radiation effects, they are first-order effects arising from any motions (passive or active) of charged particles. Only in this way is the claim of “causality violation” answered, so it’s unfortunate that neither of the rebuttal papers published by Phys Lett A mentioned it.

Return to MathPages Main Menu