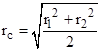|
Bisecting Plane Figures |
|
|
|
The one saith, This is my son that liveth, and thy son is the dead; and the other saith, Nay, thy son is the dead, and my son is the living. And the king said, Bring me a sword. |
|
1 Kings 3:23 |
|
|
|
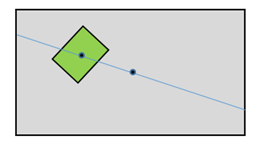
Suppose a rectangular cake has special decorative frosting on one rectangular region, and we wish to cut the cake along a single straight line in such a way that each side contains exactly half of the cake, and also half of the special frosting. This is accomplished by cutting along the line through the geometric centers of the two rectangular regions, as shown below. |
|
|
|
|
|
|
|
This works because every rectangle is an “even” shape, in the sense that the radial distance of the perimeter from the centroid satisfies r(θ) = r(-θ). As a result, every line through the centroid cuts the rectangle into two equal areas. The same applies to regular hexagons, octagons, ellipses, etc., but not to triangles, pentagons, or other “odd” shapes. (By the way, since the frosting is only on the top surface, this problem precludes the wise-guy solution of slicing the cake along the plane half-way between the top and bottom of the cake.) |
|
|
|
The radio show “Car Talk” posed a somewhat similar puzzle in 2012 involving a rectangular tray of brownies with a rectangular piece cut out of the interior, as illustrated below. |
|
|
|
|
|
|
|
The question posed was “How can you, with one cut of the knife, cut the brownies in half?” In this puzzle there is no stated requirement for each “part” to contain an equal amount of the cutout region, so there are actually infinitely many different straight lines that bisect the area of the brownies (as explained below). Also, the stated question didn’t actually specify that the cut must be along a straight line, and in addition it’s not entirely clear what is meant by “one cut of the knife”. If we cut along a line that begins at the edge of the tray and passes through the empty region and then continues (along the same line) through another region of the brownie until reaching the edge of the tray, is this considered one cut or two? Suppose the interior rectangle was nearly as large as the entire tray, so the remaining brownie consists of just a narrow rectangular path along the edge of the tray, and we make cuts on opposite sides, as shown below. |
|
|
|
|
|
|
|
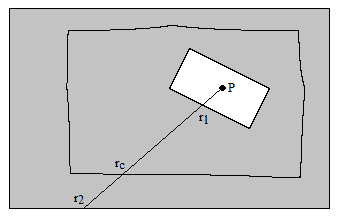
Would this be considered one cut, or two? Granted, both cuts are along the same straight line, but the question did not ask for two cuts along a single straight line, it asked for a “single cut”, and not necessarily straight. One could argue that a “single cut” must consist of a single unbroken cut, so the only solution (in this case) would be to cut around the perimeter. The same approach could be applied in the general case, as illustrated below. |
|
|
|
|
|
|
|
To draw the cut line we arbitrarily selected a point P inside the cutout region and plotted all the points at a distance rc from that point, where rc is the root mean square of the distances (along the same ray) from P to the inner and outer boundaries, denoted by r1 and r2 in the figure above. This ensures that the incremental areas swept out by the ray rotating about the point P inside and outside the cut line are equal. This follows from the fact that the incremental triangular area swept out by a segment of length r rotating by an incremental angle dθ about the point P is (r/2)rdθ, and so equating the areas inside and outside rc results in the condition |
|
|
|
|
|
|
|
and therefore |
|
|
|
|
|
Thus for any choice of the point P we get a single continuous cut that splits the brownie into two equal areas. This is arguably the only acceptable answer to the Car Talk puzzle as stated (at least the only generally applicable one, for any size of the interior cutout), since the question required a “single cut”, and of course it did not specify that the single cut had to be along a straight line. |
|
|
|
However, one suspects that the question Car Talk intended to ask was “How can you, by cutting along a single straight line, cut the brownies in half?” This differs from the question that was actually asked in two respects. First, it eliminates the problematic requirement for a “single cut”, and second, it adds the requirement for the cutting to all lie along a single straight line. It still differs, though, from our original question about cutting the cake, because (as noted above) it doesn’t specify that each part gets an equal amount of the cutout region. Without that stipulation, there are obviously an infinite number of straight lines the bisect the brownies into two equal areas. To see this, consider a line, with fixed orientation, sweeping across the tray, and note that all of the area will initially be on one side of the line, and then, after the line has swept all the way across the tray, all the area will be on the other side of the line. The area on one side is continuously increasing as we slide the line, so there must be a position where exactly half the area has been passed. This applies to any orientation of the line, so we can cut the brownies in half along a line at any angle we choose. In fact, this same reasoning applies to more general shapes, including triangles, etc. |
|
|
|
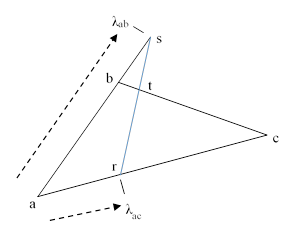
We might ask whether, for a triangular cake with a triangular region of special decorative frosting, there exists a straight line that divides both the outer and the inner triangle into equal areas (analogous to the line through the centroids of rectangles). Note that the line need not pass through the centroids, but it must bisect each of the triangles into equal areas, which is a stronger condition than simply bisecting the outer region into equal areas. To answer this question, let’s first consider how to find the lines that divide a given triangle into two equal areas. Consider the triangular region shown below. |
|
|
|
|
|
|
|
The symbol λab is the fraction of the distance from a to b where the point s is located. As s ranges from a to b, the value of λab ranges from 0 to 1. The value of λac is defined similarly based on the position of point r. We also note the area relation Aabc = Aasr + Asbcr. Now, in terms of these parameters, and noting the area of a triangle is half the product of any two edge lengths times the sine of the angle between them, we have |
|
|
|
|
|
|
|
It follows that the area is cut into equal parts if |
|
|
|
|
|
|
|
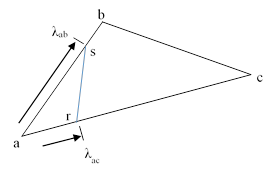
Now consider a triangular cake with a triangular region with special frosting. By moving a point along the perimeter of the outer triangle, and using the above relation to determine the corresponding point on the next clockwise edge, we can create the continuous sequence of lines, each of which bisects the area of the outer triangle. These lines rotate continuously through a complete revolution, and sweep through the entire interior of the outer triangle, as shown in the figure below. |
|
|
|
|
|
|
|
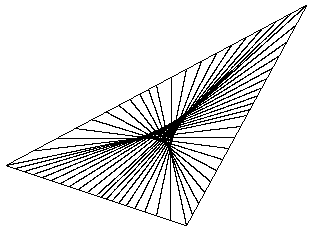
Hence they sweep through any interior figure, including the internal triangle, so we can find one of these lines that bisects the area of the internal triangle. An example is shown in the figure below. |
|
|
|
|
|
|
|
For any value of λca between 0.5 and 1 we can compute the value of λcb such that λcaλcb=1/2, which gives a line bisecting the area of the outer triangle, and then we can compute the points of intersection of this line with the sides of the inner triangle, from which we get the values of λed and λef. Our objective is to determine a value of λca such that λedλef = 1/2. The coordinates of the vertices of the outer triangle in the figure above are (-7,-2), (8,6), and (2,-5), and the coordinates of the vertices of the inner triangle are (1,-1), (3,2), and (4,0). From this we can determine that the values of λca that satisfy the stated conditions must be a root of the quartic polynomial |
|
|
|
|
|
|
|
The only real root in the range from 0.5 to 1 is λca = 0.9252391... , and this is depicted in the figure above, showing that it does indeed bisect both the overall cake and the region of special frosting. |
|
|
|
Incidentally, although we’ve restricted the values of the λ parameters to the range 0 to 1, so that the interpolated points are between the vertices, the same equations apply formally to arbitrary values, based on the extrapolated edges of the triangles. For example, in the triangle below we have chosen a value of λab greater than 1. |
|
|
|
|
|
|
|
Just as before we have the area relation Aabc = Aasr + Asbcr, with the understanding that these are signed areas, with the regions enclosed by clockwise paths defined as positive. Thus the region stb is positive for the triangle asr but negative for the quadrilateral sbcr. The difference between the signed area of the quadrilateral sbcr and the triangle asr is |
|
|
|
|
|
|
|
and hence these two signed areas are equal if λcaλcb=1/2 for any values of the parameters, and we can say that the line rs bisects the area of the triangle abc. On this basis, the other real root of the quartic polynomial, λca = 0.333889..., gives another solution, albeit purely formal, since there is no negative cake. There are also two complex solutions. |
|
|