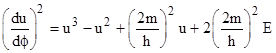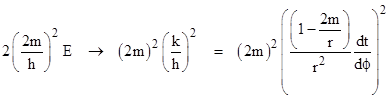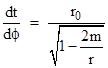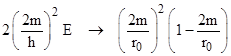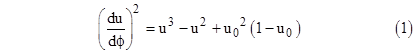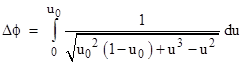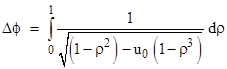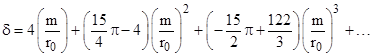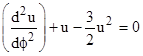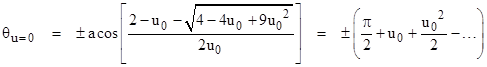|
Derivations of Relativistic Light Deflection |
|
|
|
One ought not to have to care |
|
so much as you and I |
|
care when the birds come round the house |
|
to seem to say good-bye. |
|
†††††††††††††††††††††††††††††††††† Robert Frost |
|
|
|
In the note on Anomalous Precession we derived the relativistic equation of motion for a massive test particle in a spherically symmetrical gravitational field of a mass m. In terms of the usual Schwarzschild coordinates r,θ,ϕ,t (and using geometrical units so that c = G = 1) we considered the metric in the equatorial plane (θ = π/2) |
|
|
|
|
|
|
|
and integrated two of the geodesic equations to find constants k and h (corresponding to the energy and angular momentum) given by |
|
|
|
|
|
|
|
We then defined the auxiliary parameter u = 2m/r, and derived the equation of motion |
|
|
|
|
|
|
|
where E = (k2 − 1)/2. We used this equation to determine the precession of bound orbits of material objects (such as the planet Mercury orbiting the Sun), but the same equation can be used to determine the deflection of light, provided we adapt it to account for the fact that dτ = 0 along the path of a light pulse. First, we note that k and h become infinite, so the coefficient of u in the equation of motion goes to zero. The constant coefficient has E (and hence k2) in the numerator and h2 in the denominator, so we need to evaluate that coefficient. In the limit as dτ goes to zero that coefficient goes to |
|
|
|
|
|
|
|
Since this is a constant, we can evaluate it at any convenient point, such as the perigee of the light path, i.e., the point of nearest approach to the central mass. We will let r0 denote the radial coordinate of that point, and u0 the corresponding reciprocal coordinate. From the metric equation with dr = dτ = 0 (at the perigee) we have |
|
|
|
|
|
|
|
Substituting this into the previous expression (evaluated at r = r0), we find that the constant coefficient of the equation of motion for a light-like path goes to |
|
|
|
|
|
|
|
Therefore, our light-like pulse satisfies the equation of motion |
|
|
|
|
|
|
|
The angular travel from the perigee (u = u0) out to infinity (u = 0) would be simply π/2 if the path was a straight line, but it will exceed this by a slight amount due to the effect of the gravitational field. To determine this amount, we re-arrange the equation of motion and perform the integration |
|
|
|
|
|
|
|
Making a change of variables to ρ = u/u0 this can be written as |
|
|
|
|
|
|
|
This is precisely the same integral we found by a completely different method in the note on Bending Light, leading to the overall deflection |
|
|
|
|
|
|
|
Another (less rigorous) approach is to differentiate equation (1) again with respect to ϕ, and divide through by 2(du/dϕ) to give |
|
|
|
|
|
|
|
In the note on Analysis of Relativistic Orbits we showed how, by expressing u(θ) as a power series in θ, substituting into this equation, and setting the coefficient of each power of θ to zero, we get conditions on the coefficients leading to the approximate solution |
|
|
|
|
|
|
|
As a check, we can substitute this into the preceding differential equation and show that the left hand side differs from 0 only by terms on the order of u03 and u04. We also note that this solution gives u(0) = u0 (which is not true for the approximate solutions of most published derivations). The asymptotes of the path correspond to u = 0 (i.e., as r goes to infinity), so we need only solve the quadratic |
|
|
|
|
|
|
|
for cos(θ) and then take the inverse cosine to give the angles of the asymptotes. The result is |
|
|
|
|
|
|
|
To the lowest order, the difference between these two angles exceeds π by 2u0 = 4m/r0, which is the relativistic deflection to this level of approximation. Unlike the method of direct integration described above, this method canít be used to give higher orders, because the expansion is already based on an approximate solution of the differential equation. |
|
|