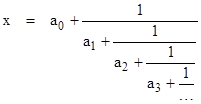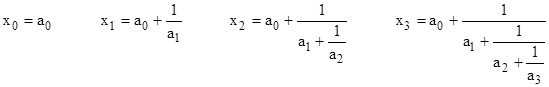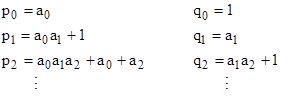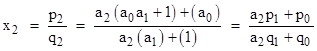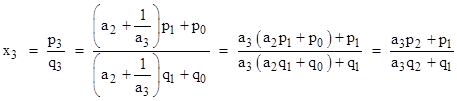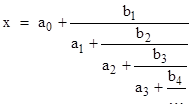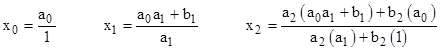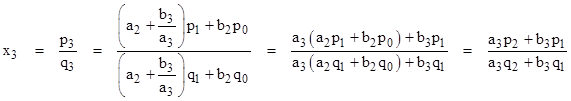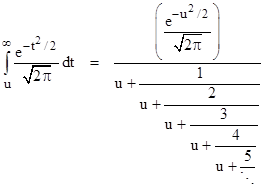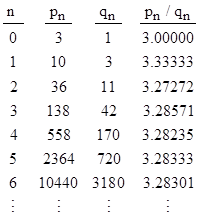Continued Fractions and Weighted Mediants

Wherefore, my beloved, as ye have always obeyed, not as in my presence only, but now much more in my absence, work out your own salvation...

                                                                                      Philippians, 2:12

A simple continued fraction for the quantity x is an expression of the form

where the a_j coefficients are ordinarily positive integers. The convergents of this continued fraction are defined as the partial results

and so on. Each convergent x_n can be written as a simple fraction p_n/q_n where

Notice that x₂ can be expressed as

Furthermore, it’s clear from the definitions of the convergents that if we have an expression for x_n in terms of a₀, a₁, ..., a_n, then the value of x_n+1 is given by simply replacing a_n with a_n + 1/a_n+1. Thus, for example, we can write x₃ using the above expression for x₂ as follows

By induction it follows that

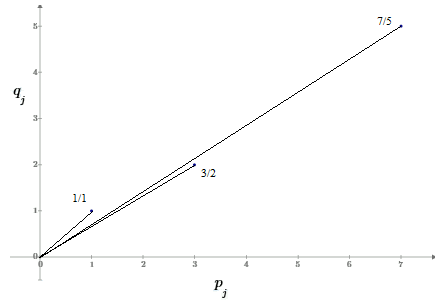
for all n > 1. Thus each convergent of a simple continued fraction is the weighted mediant of the previous two convergents. This is depicted in the figure below for the first three convergents of the simple continued fraction for the square root of 2:

In this case the coefficients are a₀ = 1 and a_j = 2 for all j>0. In general, the convergents always alternate on either side of the asymptotic value, because the weighted mediant is always between the two arguments. Notice that if a_n were equal to zero, then x_n would equal x_n−2, whereas for positive values of a_n the value of x_n is weighted toward x_n−1 (and approaches x_n−1 as a_n goes to infinity). The coefficient a_n is always the largest integer such that x_n is still on the opposite side of the asymptotic value from x_n−1.

A similar approach can be taken to evaluating more general forms of continued fractions. For example, consider a continued fraction of the form

The first few convergents are

Therefore, letting x_n = p_n/q_n for the ratios written in this form, we have

By similar reasoning to our analysis of simple continued fractions, we can say that the expression for x₃ is given by replacing a₂ in this expression with a₂ + b₃/a₃. This leads to

Again by induction it follows that, in general, we have

for all n > 1. This shows (again) that each convergent is a weighted mediant of the two prior convergents.

As an example, suppose we wish to evaluate the area under the upper tail of the normal curve from some u to infinity using Laplace’s expression

We can evaluate the numerator (the quantity in parentheses) directly, so it only remains to determine the value of the continued fraction in the denominator. For this we have a_j = u and b_j = j for all j. Thus beginning with the initial values p₀ = u and p₁ = u²+1 we can compute all subsequent values of p_j using the recurrence p_n = up_n−1 + np_n−2. Likewise we have the initial values q₀ = 1 and q₁ = u, and we can compute all subsequent values of q_j using the recurrence q_n = uq_n−1 + nq_n−2. To illustrate, with u = 3 we get

Thus we can recursively compute the denominator in Laplace’s formula to any desired precision.

Return to MathPages Main Menu