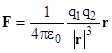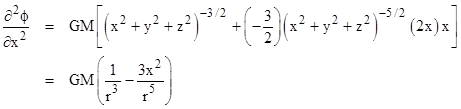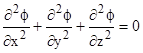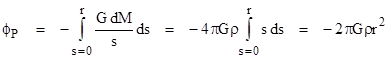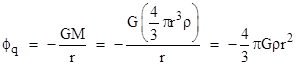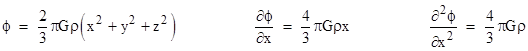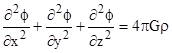Poisson’s Equation and the Universe

They shaved her head.  She was torn between Jupiter

and Apollo.  A messenger arrived...

                                                             Bob Dylan

In an article called “Einstein and Pi”, written in observance of March 14, which happens to be both Einstein’s birthday and Pi Day, Sean Carroll noted that the transcendental number π appears in Einstein’s gravitational field equations (with a certain choice of units), whereas it does not appear in Newton’s equation for the force of gravity. Carroll says

The real question is, why does π make an appearance when we make the transition from Newtonian gravity to general relativity?

However, Carroll goes on to note that π actually does appear in Newton’s law, when written in the form of Poisson’s equation, which is the Newtonian analog of Einstein’s field equations. Therefore, the appearance of π doesn’t actually correspond to the transition from Newtonian gravity to general relativity. To salvage a link between Einstein and the number π, one might argue that the factor of 4π is at least somewhat related to the transition to general relativity because it appears when we express Newton’s law in terms of a potential field, which conceptually leads on to Einstein’s field theory of gravity. But the factor 4π already appears in Gauss’s law ∇×g = −4πGρ for Newtonian gravity, which doesn’t refer to the potential, it simply expresses a relation involving the divergence of the gravitational acceleration vectors g defined by Newton’s basic “inverse-square” law g = −GMr/|r|³. Gauss’s law becomes Poisson’s equation when coupled with the fact that we can define a scalar field ϕ such that g = −∇ϕ, but the factor of 4π is already present. Also, the appearance of π in an equations of physics is to some extent conventional, dependent on the choice of units. For example, Coulomb’s law for the electrostatic force between two charged particles, analogous to Newton’s inverse square law for the force of gravity between two masses, written in SI units is

and Poisson’s law is written as ∇²ϕ = −ρ/ε₀. Thus, one might just as well ask why π appears in the law for the point-to-point force at a distance, but not in Poisson’s equation for the electric potential field.

Even though the connection between π and “the transition to general relativity” is dubious, it’s still interesting to examine why, within the Newtonian context, we get a factor of 4π when going from the basic expression for the potential to Poisson’s equation. In other words, why π appears in Poisson’s equation ∇²ϕ = 4πGρ, whereas it does not appear in what Carroll calls “Newton’s equation” ϕ = −GM/r for the Newtonian gravitational potential. Carroll says

Whereas we were originally concerned (in Newton’s equation) with the gravitational effect of a single body [of mass M] at a distance r, we’re now adding up all the accumulated effects of everything in the universe... The reason π comes into Poisson’s equation and not Newton’s is that Newton cared about the force between two specific objects, while Poisson tells us how to calculate the potential as a function of a matter density spread all over the place...

This is completely daft, for several reasons. First, Poisson’s equation simply relates the Laplacian of the potential at any given point to the density of matter at that point. It does not depend at all on the matter density at any other point, let alone the matter density “of everything in the universe”. Second, when we want to calculate the potential due to the matter density “spread all over the place” we actually use what Carroll calls Newton’s equation, rather than Poisson’s equation. In fact, Newton’s equation is the solution of the Poisson equation. Note that Newton’s equation is not limited to just the interaction between two specific objects, it can be used to compute the potential due to any number of objects. (The total potential is just the sum of the individual potentials.)

Setting all that aside, Carroll’s “explanation” for the 4π factor is that we must integrate “all over the place” in terms of spherical surfaces, and since the surface area of a sphere is 4πr², this explains (according to Carroll) the 4π factor. But that explanation is misleading at best, because (as noted) Poisson’s equation actually refers only to the mass density at a specific point. It can be shown (see below) that the mass at any other points does not contribute anything to the Laplacian at that point. So how can we correctly explain the factor 4π? The answer is not as trivial as one might think (e.g., it is often derived by invoking an identity involving the Dirac delta function), and leads to some interesting conundrums – as well as to an actual connection with Einstein and his famous cosmological constant.

The most straightforward derivation of Poisson’s equation makes use of the divergence theorem, to be discussed below, but first we will present a perhaps more intuitive derivation that makes use of the most important and familiar of Newton’s theorems on gravity, namely, his Proposition 71. This states that the force of gravity exerted by a spherical shell on a point outside the shell is the same as if all the mass was located at the center. An immediate corollary is that the force of gravity exerted by a spherical shell on a point inside the shell is zero. Admittedly these propositions are not obvious (Newton himself said he was surprised by them), but they are so well known that they may serve for purposes of clarifying the source of the 4π factor in Poisson’s equation.

First, it’s easy to show that a quantity of mass M at any non-zero distance r from the point P contributes nothing to the Laplacian of the gravitational potential ϕ = −GM/r at P. We simply take the partial derivative of ϕ with respect to x

and then take the second partial derivative to give

Adding this to the corresponding expressions for the second partial derivatives with respect to y and z, we arrive at the Laplace equation

The expression on the left side is called the Laplacian of ϕ. This equation is linear, so solutions are additive. Thus, if the density of mass at point P is zero, this equation applies, regardless of what mass may be present at any other surrounding locations. This was based on the expression ϕ = −GM/r for any non-zero value of r, but if r = 0 the potential is infinite, which stands to reason, because in that case the mass M is located in a region of zero volume at the point P, so the density is infinite at that point. The case we wish to consider is with some non-zero but finite mass density ρ at the point P. For any continuous mass distribution, it follows that there is a non-zero region, containing the point P, in which the density is essentially constant.

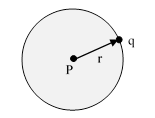
To determine the value of the Laplacian at the point P where the mass density is ρ we need to evaluate the partial derivatives of ϕ with respect to x, y, and z. To do this, we must consider how ϕ changes as we move an incremental distance r away from P to the neighboring point q, as illustrated in the figure below.

If the sphere of radius r centered on P was devoid of matter, the value of the Laplacian would be zero throughout that region (as we proved above), so none of the matter outside that sphere contributes anything to the Laplacian at P. Thus we need only consider the mass within that infinitesimal sphere in order to evaluate the Laplacian at the point P. First, note that the potential at P consists of contributions from each infinitesimal spherical shell surrounding that point. By Newton’s proposition 71 we know that the force of gravity exerted by a spherical shell on any point in its interior is zero, and hence the potential due to that shell is constant in the interior. Since the surface area of a sphere of radius s is 4πs², the incremental mass dM of a shell of radius s and incremental thickness ds is dM = 4πρs²ds, and therefore the potential at P due to all the mass shells from s = 0 to r is given by the integral

Also, from Newton’s proposition 71, we know that the potential at q is the same as if all the mass was located at the point P, so we have

The potential ϕ(r) at an infinitesimal distance r from P relative to the potential at P is therefore

We can evaluate the partial derivatives of this function with respect to x, y, and z at the origin. For example, the derivatives with respect to x are

and similarly for y and z. Each partial contributes (4/3)πGρ, so we arrive at Poisson’s equation

In essence, we evaluated the partial derivatives by considering the effect of moving from the center to the perimeter of an infinitesimal sphere in any direction, accounting for the potential due to that tiny sphere (of constant density) at both positions.

Of course, as mentioned above, Poisson’s equation is really a direct consequence of the divergence theorem, which states that for any vector field g and any enclosed region of space we have

Let g denote the acceleration of gravity for a unit mass, and consider a small spherical region of radius r. The region is small enough that the density ρ in the region is constant, and the mass in the region is M = ρV where V is the enclosed volume. Making use of Newton’s proposition 71 again, the acceleration of gravity everywhere on the surface of this sphere has magnitude GM/r² pointing directly inward, and the surface area is 4πr² with the normal pointing directly outward, so the left hand integral is −4πGρV. Also, for a sufficiently small region the gradient of g is constant within that region, so the right hand integral is (∇×g)V. Hence we immediately have Gauss’ law ∇×g = −4πGρ, from which Poisson’s equation follows upon replacing g with −∇ϕ.

However, if we try to apply Poisson’s equation to the entire universe, we encounter difficulties (closely related to Olber’s paradox). Suppose the mass density ρ of the universe is essentially constant on the largest scale, and that the universe is flat and extends to infinity in all directions. In that case the gravitational potential is infinite. Furthermore, by symmetry the potential should have the same value everywhere, so the partial derivatives and hence the Laplacian would be zero, contradicting Poisson’s equation. Newton himself was already aware of this problem, as it was brought to his attention by Richard Bentley, who wondered if the present universe and solar system that we observe today could have arisen by mechanical means from an initial state of uniformly distributed matter, the extent of the original matter being either finite or infinite. Newton rejected the finite possibility, since he thought an “island universe” would collapse on itself into a single body at the center. (He apparently didn’t consider oscillating configurations.) He thought it more plausible that matter was originally spread evenly throughout an infinite universe. He wrote in his first reply to Richard Bentley (Dec 10, 1692)

If the matter was evenly diffused through an infinite space, some of it would convene into one mass and some into another so as to make an infinite number of great masses scattered at great distances from one another throughout all that infinite space. And thus might the Sun and fixed stars be formed...

Bentley objected that if the original distribution really was perfectly uniform there would be no reason for anything to move (being pulled equally in all direction), so he questioned why Newton thought the matter would cluster together. Newton answered (Jan 17, 1693)

[It is very difficult] to suppose that all the particles in an infinite space should be so accurately poised one among another as to stand still in a perfect equilibrium. I reckon this as hard as to make an infinite number of needles stand accurately poised upon their points. Yet I grant it possible, at least by a divine power, and if they were once so placed I agree with you that they would continue in that posture without motion for ever... When therefore I said that matter evenly spread through all spaces would convene by its gravity into one or more great masses, I understand it of matter not resting in an accurate poise.

But Bentley had already anticipated this, saying that even if the initial distribution was not perfectly uniform, each particle would still be subject to an infinite pull in every direction, and since (as Bentley supposed) all infinites are equal, the matter would not move.  To this Newton replied

I conceive the paralogism lies in the position that all infinites are equal...  If a body stood in equilibrium between any two equal and contrary attracting infinite forces, and if to either of those forces you add any new finite attracting force, that new force, how little so ever, will destroy the equilibrium and put the body into the same motion into which it would put it were those two contrary equal forces but finite or even none at all...  the principle that all infinites are equal is a precarious one.

The questions raised by Bentley seemed to catch Newton’s interest, because he wrote a follow-up letter over three weeks later (Feb 11, 1693)

The hypothesis of deriving the frame of the world by mechanical principles from matter evenly spread through the heavens being inconsistent with my system, I had considered it very little before your letters put me upon it, and therefore trouble you with a line or two more about it...  I would now add that the hypothesis of matter being at first evenly spread through the heavens is, in my opinion, inconsistent with the hypothesis of innate gravity without a supernatural power to reconcile them... for if there be innate gravity it is impossible now for the matter of the earth and all the Planets and stars to fly up from them and become evenly spread throughout all the heavens without a supernatural power.  And certainly that which can never be hereafter without a supernatural power could never be heretofore without the same power.

This is an interesting argument, related to well-known conundrums involving the second law of thermodynamics, time-reversibility, and the original state of the universe. Newton seems to be saying that since a congealed arrangement of matter, collapsed under the influence of gravity into isolated bodies, could never spontaneously evolve into a uniform distribution, it follows that a uniform distribution could never have existed in the past either, because the laws of mechanics are temporally reversible. To use his own earlier phrase, though, this is a precarious hypothesis. We think it impossible that all the uniformly distributed air molecules in an enclosure would spontaneously cluster into one corner, and yet if the air was originally clustered in one corner and then released, it would spread uniformly throughout the room, i.e., the reverse of a process that we consider to be impossible. But elsewhere Newton himself had commented on the probabilities involved in such scenarios, saying (essentially) that systems are much more likely to progress toward equilibrium than away from it.

Incidentally, after earnestly discussing “innate gravity” with Bentley in several letters, Newton made the famous comment that the idea of innate gravity “is to me so great an absurdity that I believe no man who has in philosophical matters any competent faculty of thinking can ever fall into it.” Ironically, this is the only part of the Bentley correspondence that Carroll quoted in his article, even though the remainder of the letters was (arguably) more relevant to Poisson’s equation. (The other main topic of those letters was a consideration of Plato’s proposal for the origin of the solar system, which we’ve discussed elsewhere.)

Over two centuries later, Einstein took up the subject of gravitation in an infinite universe, which he discussed in his 1917 paper “Cosmological Considerations in the General Theory of Relativity”, which begins with a review of Bentley’s paralogism for Newtonian mechanics:

It is well known that Poisson’s equation... is not a perfect substitute for Newton’s theory of action at a distance. There is still to be taken into account the condition that at spatial infinity the potential ϕ tends toward a fixed limiting value...  Newton’s limiting condition of constant ϕ at spatial infinity leads to the view that the density of matter becomes zero at infinity... the mean density must decrease toward zero more rapidly than 1/r².  In this sense, therefore, the universe according to Newton is finite...

This implies that Newtonian gravity is only consistent if we stipulate that the mass density goes to zero as we move away from some central region. As we’ve seen, Newton already rejected this, on the grounds that all the matter would tend to collapse into a single body at the center, but it’s true that Newton didn’t really offer any plausible mechanistic alternative, and indeed the whole purpose of his correspondence with Bentley was to identify aspects of the world that require a supernatural explanation (i.e., divine intervention). Einstein too gives arguments for why this “Newtonian” cosmology is untenable, and concludes that

It hardly seems possible to surmount these difficulties on the basis of the Newtonian theory. We may ask ourselves the question whether they can be removed by a modification of Newtonian theory... [Suppose that] in place of Poisson’s equation, we write

where λ denotes a universal constant. If ρ₀ be the uniform density of a distribution of mass, then

is a solution...  If, without making any change in the mean density, we imagine matter to be non-uniformly distributed locally, there will be, over and above the ϕ with the constant value [noted above], an additional ϕ, which in the neighborhood of denser masses will so much the more resemble the Newtonian field as λϕ is smaller in comparison with 4πGρ.

This is the first appearance of Einstein’s famous cosmological constant. In the remainder of the paper he applies the analogous considerations in the context of general relativity, to arrive at a static uniform distribution that satisfies the field equations (heedless of Newton’s warning that this would be unstable, equivalent to balancing infinitely many needles on their points), and found that the analogous modification to his field equations was required. Specifically, he found that the covariant divergence of the “left side” of the field equations would still vanish if the left side was augmented by an additional term

The sign of the right hand side is conventional, dependent on the sign conventions in the definitions of the Ricci tensor (as either plus or minus the contraction of the Riemann curvature tensor). In fact, even the factor 8π is conventional, just as the factor of 4πε₀ in Maxwell’s equations depends on the choice of units.

Of course, in Einstein’s paper of 1917 he proposed a cosmological model that presumably never occurred to Bentley or Newton, namely, that the universe is a closed spherical manifold, so it is finite and yet unbounded. From a theoretical standpoint this model is very appealing, and still has ardent proponents – especially among those who favor a relational basis for inertia – but the current astronomical observations seem inconsistent with a closed finite universe.

Another possible escape from “Bentley’s conundrum” (and Olber’s paradox) is a hierarchical distribution of matter in an infinite universe. Oddly enough, this had already been considered by Edgar Allen Poe in the 1840s, in the interesting book “Eureka”. In the 1920’s the philosopher Franz Selety championed this model, and corresponded with Einstein about it. In 1922 Einstein summarized his view of the idea:

From the standpoint of Newton’s theory there is, it must be conceded, something to the hypothesis of a “molecular-hierarchical” structure for the universe of stars... this hypothesis unassailably explains the non-luminosity of the background sky [i.e., Olber’s paradox] and avoids conflict with Newton’s law [i.e., Bentley’s conundrum] without conceiving matter as islands in empty space. Even from the point of view of the general theory of relativity, the hypothesis of a molecular-hierarchical structure of the universe is possible. Nevertheless, from the standpoint of this theory the hypothesis should be regarded as unsatisfactory...

His reason for regarding a hierarchical structure as unsatisfactory was that he still held to the Machian belief that the world’s metric and inertial field must be attributed entirely to “physical causes”, i.e., to the distribution of mass-energy in the universe, with no prior background, and he believed this is fulfilled (in a sense) within the context of general relativity only if the mean density of matter is positive and finite and the universe is spatially closed. He noted that nearly all his contemporaries were content to accept the world’s metric as a given thing, although he added (with typical self-assurance) that “To later generations, this contentedness will seem incomprehensible”. On the other hand, his own enthusiasm for Mach’s principle and the idea of relationism waned in later years.

Return to MathPages Main Menu