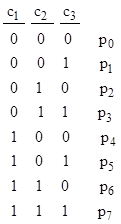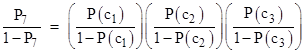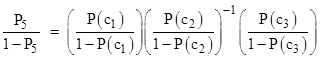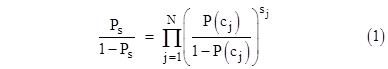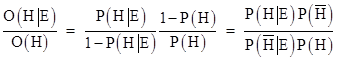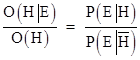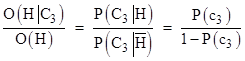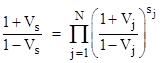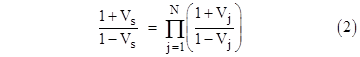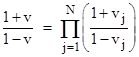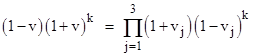Probabilities, Odds, and Relativistic Speeds

Your grace hath laid the odds o' the weaker side.

                                                     Shakespeare

In another note we discussed combining probabilities. Here we consider the same subject from a slightly more abstract and general standpoint, and note a correspondence with the composition of relativistic velocities.

Consider a set of N+1 logical variables C₀, C₁, ..., C_N, each of which has either the value T (true) or F (false). We stipulate that each of the 2^N+1 possible configurations has a fixed probability, and furthermore that the probability of any configuration is the same as that of the complementary configuration. In other words, the system is invariant under exchange of True and False for all the variables. Next we define

where over-bars signify logical negation. Thus c_j is true if and only if C_j agrees with C₀.  There are 2^N possible configurations of the variables c₁ to c_N, and we can assign a fixed probability to each configuration. For example, with N = 3 we have the following 8 possible configurations (using 1 to denote True and 0 to denote False), each with some definite probability.

Now we stipulate that c₁, c₂,..., c_N are independent logical variables, meaning that the probability of the intersection of any subset of these events equals the product of the probabilities of the individual variables. (Note that pairwise independence is not sufficient to ensure complete independence.) These requirements fully determine the probabilities for each of the eight possible system configurations in terms of the probabilities of the individual variables. For example, the value of p₅ in the table above is given by

If all three of the variables C₁, C₂, and C₃ agree with each other, what is the probability that they agree with C₀? The answer is simply p₇/(p₀ + p₇), since p₀ and p₇ are the probabilities of the two configurations in which all three of the variables have the same value, and p₇ is the configuration in which they agree with C₀.  Thus, letting P₇ denote the probability in question, we have

Taking the reciprocal and subtracting 1 from both sides, it follows that (1−P₇)/P₇ = p₀/p₇, and inserting the values of p₀ and p₇ we get

On the other hand, suppose C₁ and C₃ agree with each other, but C₂ has the opposite value. In this case, what is the probability that C₁ and C₃ agree with C₀? We will denote this probability by P₅. The answer is p5/(p2 + p5), because p₂ and p₅ are the probabilities of the two configurations in which C₁ and C₃ agree and C₂ differs. Thus we get

In general, we can partition the N values of C_j (j=1 to N) into two sets A and B according to their values, and ask what is the probability that C₀ agrees with the value of the variables in A. For convenience we create a vector s, and put s_j equal to +1 if C_j is in A, and put s_j = −1 if C_j is in B. Then the probability in question is

Incidentally, if P(X) is the probability of an event X, then the “odds” O(X) of that event are defined as P(X)/(1−P(X)). Suppose the odds of a given hypothesis H are O(H), and we want to know how the odds of H would be affected given some new evidence E. Thus we want O(H|E), so the effect of evidence E is to multiply the original odds by the factor O(H|E)/O(H). This is sometimes called a Bayes factor. We have

Noting the identities

we find that the Bayes factor satisfies the relation

In our previous example, with N = 3, the hypothesis H was that C₀ is True, and we can consider the effect of the “evidence” E corresponding to (say) C₃ being True. The probability of C₃ being True given that H is True is simply P(c₃) = p₁ + p₃ + p₅ + p₇, because this is the sum of the probabilities for the configurations in which C₃ agrees with C₀. On the other hand, the probability of C3 being True given that H is False is the complement of this, i.e., it is 1–P(c₃) = p₀ + p₂ + p₄ + p₆, because this is the sum of the probabilities for the configurations in which C₃ does not agree with C₀. Thus the Bayes factor for the evidence C3 is

For independent variables, each piece of evidence contributes a factor of this form, consistent with our previous result.

As an aside, we note some interesting aspects of the conceptual transition from the system of N+1 logical variables C_j to the system of N logical variables c_j. Recall that we defined c_j for j = 1 to N as the condition that C_j agrees with C₀, and we stipulated that the probability of agreement with C₀ is independent of the value of C₀.  Thus given the 2^N+1 possible configurations {C₀,C₁,...,C_N} we assign the same probability to complementary configurations. In effect, we treat each configuration and its complement as “the same configuration”. This is reminiscent of how we model elliptical geometry as the points on the surface of an ordinary sphere but with the stipulation that opposite (anti-podal) points on the sphere are treated as “the same point”. Having imposed this complementary symmetry, we can consider just the 2^N configurations {c₁,c₂,...c_N}, and we then stipulate that these N variables are completely independent (not just pairwise independent). We’ve seen that these stipulations, together with specified values of the N probabilities P(c_j), are sufficient to completely determine the probabilities of each of the 2^N possible configurations of the c_j, and hence each of the 2^N+1 configurations of the C_j. Each configuration of the c_j represents two complementary configurations of the C_j, and we assign half the probability of the former to each of the latter. The system resulting from these stipulations is formally symmetrical in the C_j for j = 1 to N, but obviously not symmetrical with C₀, unless all the probabilities P(c_j) equal 1/2. This corresponds to an asymmetry involving relativistic velocities discussed below.

There’s an interesting formal correspondence between relation (1) and the relativistic speed composition formula. Suppose that for each probability P we define a new variable V by the relation V = 2P−1. The above relation is

In this form the reciprocation of the factors in the product can be equivalently given by simply negating the respective V parameter. Therefore, if we re-define V_j by the relation V_j = ±(2P_j−1) where the sign is positive if C_j is in A and negative if C_j is in B, we can omit the exponent s_j and write the above relation in the form

Now consider a set of N particles moving at constant speeds along a single line. Let v₁ denote the signed speed of one particle relative to some given system K₀ of standard inertial coordinates, and let v₂ denote the signed speed of a second particle in terms of the standard inertial rest frame coordinates K₁ of the first particle. Similarly let v₃ denote the signed speed of a third particle in terms of the standard inertial rest frame coordinates K₂ of the second particle, and so on. Then, according to the special theory of relativity, the composition of all these speeds (i.e., the speed of the Nth particle in terms of K₀) is the speed v given by

This is formally identical to (2), showing that the composition of (co-linear) speeds in special relativity corresponds to the composition of (re-scaled) probabilities for independent conditionals in probability theory. In another note we discussed a different mapping, P = v²,  between probabilities and velocities, whereby the square of a velocity (in units with c = 1) is identified with a probability, and we showed there how the relativistic combination of perpendicular velocities corresponds to the basic law of probability for independent events. Here we’ve described another correspondence, this one based on the linear mapping P = (v+1)/2, applied to co-linear velocities.

These two mappings are not as incommensurate as they might seem, because the combination formula for three mutually perpendicular speeds (presented in the other note) is

which can be factored as

where k = 1 for perpendicular speeds, and k = −1 for co-linear speeds.

As mentioned above, there is an asymmetry between the logical variables C_j for j = 1 to N and the “reference” logical variable C₀. This mirrors the asymmetry, under reciprocation, between the velocities in the relativistic velocity composition formula discussed in the note “More Symmetry”.

Return to MathPages Main Menu